
- •1. Основные понятия, определения и теоремы теории вероятностей*
- •1.1. Алгебра событий. Основые понятия теории множеств
- •1.2. Основные определения: испытание, событие. Классификация событий
- •1.3. Классическое определение вероятности. Свойства, вытекающие из этого определения
- •Значение вероятности
- •1.4. Основные теоремы теории вероятностей
- •1.5. Зависимые и независимые события
- •2. Формула полной вероятности и формула Бейеса
- •2.1. Формула полной вероятности
- •3. Случайные величины
- •3.1. Дискретные случайные величины
- •Ряд распределения случайной величины X
- •3.4. Ожидаемое среднее значение дискретной случайной величины
- •Вычисление математического ожидания числа рекламных
- •3.5. Свойства математического ожидания случайной дискретной величины
- •Возможные исходы лотереи
- •3.6. Ожидаемое среднее значение функции случайной величины
- •Ряд распределения числа месячных продаж
- •К вычислению среднего ожидаемого значения
- •3.7. Дисперсия дискретной случайной величины
- •К вычислению дисперсии случайной величины
- •3.9. Дисперсия линейной функции случайной величины
- •4. Законы распределения дискретных случайных величин
- •Формула Бернулли. Биномиальные вероятности
- •4.3. Биномиальный закон распределения
- •Биномиальное распределение
- •Биномиальное распределение X – числа гербов, появляющихся
- •Фрагмент таблиц ряда и функции биномиального распределения
- •Биномиальное распределение числа покупателей
- •Распределения
- •4.5. Распределение Пуассона
- •Закон распределения Пуассона
- •Сравнение вероятностей, полученных по формулам Бернулли и Пуассона
- •4.6. Гипергеометрическое распределение
- •Гипергеометрический закон распределения
- •Биномиальный закон распределения
- •Гипергеометрическое распределение
- •4.7. Производящая функция
- •4.8. Мультиномиальное распределение
- •4.9. Геометрическое распределение
- •5. Непрерывные случайные величины
- •6. Законы распределения непрерывных случайных величин
- •7. Закон больших чисел
- •7.1. Принцип практической уверенности. Формулировка закона больших чисел
- •7.2. Неравенства Маркова и Чебышева
- •7.3. Теорема Чебышева (частный случай)
- •7.4. Теорема Бернулли
- •7.5. Теорема Пуассона
Сравнение вероятностей, полученных по формулам Бернулли и Пуассона
m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Рn,m=Cnmpmqn–m |
0,778 |
0,196 |
0,024 |
0,002 |
0,000 |
0,000 |
0,000 |
|
0,779 |
0,195 |
0,022 |
0,001 |
0,000 |
0,000 |
0,000 |
|∆| |
0,001 |
0,001 |
0,002 |
0,001 |
0,000 |
0,000 |
0,000 |
Сопоставление вероятностей показывает, что рассчитанные по формуле Пуассона вероятности почти совпадают с их значениями, вычисленными по формуле Бернулли. Максимальная погрешность результатов, вычисленных по формуле Пуассона, равна 0,002.
4.6. Гипергеометрическое распределение
Выше мы рассмотрели способы вычисления вероятностей появления события ровно т раз в п независимых повторных испытаниях (по формулам Бернулли и Пуассона). Теперь познакомимся с вычислением вероятности появления события ровно т раз в п зависимых повторных испытаниях. Случайная величина, определяющая число успехов в п повторных зависимых испытаниях, подчиняется гипергеометрическому закону распределения.
Пример 4.9. В урне N шаров, среди которых К белых и (N–K) черных. Без возвращения извлечены п шаров. Определим вероятность того, что в выборке из п шаров окажется т белых (и соответственно n–m черных) шаров. Изобразим ситуацию на схеме:
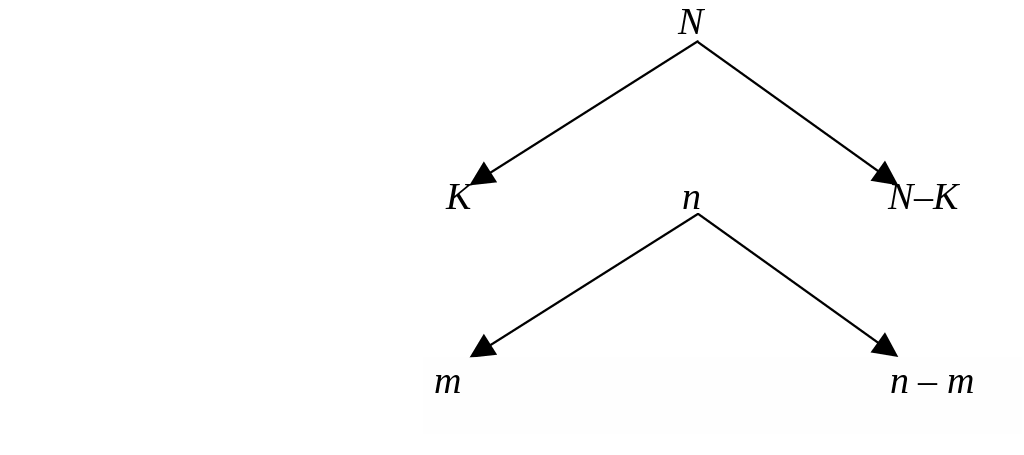
Случайная величина, интересующая нас, X = т – число белых шаров в выборке объемом в п шаров. Число всех возможных случаев отбора п шаров из N равно числу сочетаний из N по n (CNn), а число случаев отбора т белых шаров из имеющихся К белых шаров (и значит, п–m черных шаров из N–K имеющихся черных) равно произведению CKmCN–Kn–m (отбор каждого из т белых шаров может сочетаться с отбором любого из n–т черных). Событие, вероятность которого мы хотим определить, состоит в том, что в выборке из п шаров окажется ровно т белых шаров. По формуле для вероятности события в классической модели вероятность получения в выборке т белых шаров (т. е. вероятность того, что случайная величина X примет значение т) равна
 ,
(4.14)
,
(4.14)
где CNn – обшее число всех единственно возможных, равновозможных и несовместных исходов, CKmCN–Kn–m – число исходов, благоприятствующих интересующему нас событию.
Итак, вероятность появления интересующего нас события ровно т раз в п зависимых испытаниях вычисляется по формуле (4.14), которая задает значения гипергеометрического закона распределения для т = 0, 1, 2,..., п (табл. 4.8).
Таблица 4.8
Гипергеометрический закон распределения
т |
0 |
1 |
2 |
… |
n |
Р(X=m) |
CK0CN–k n/ CNn |
CK1CN–Kn–1/ CNn |
CK2CN–Kn–2/ CNn |
… |
CKmCN–K0/ CNn |
M(т) = n, (4.15)
D(m) = n (1–)[1– (n–1)/(N–1)], (4.16)
где – доля единиц с интересующим нас признаком в совокупности N, т. е. = K/N, а 1–(n–1)/(N–1) называется поправкой для бесповторной выборки.
Пример 4.10. Разыгрывается тираж выигрышного денежного займа, в котором выпушено N облигаций, из которых К – выигрышные. Некто приобрел п облигаций. Найдем вероятность того, что т из них – выигрышные.
Рассуждая в соответствии с изложенной схемой, по формуле (4.14) получим интересующую покупателя облигаций вероятность выигрыша.
Пример 4.11. Автомобили поступают в торговый салон с завода партиями по 10 штук. По соглашению сторон для экономии времени и ресурсов в торговом салоне подвергаются контролю качества и безопасности только 5 из 10 поступающих автомобилей. Обычно 2 из 10 поступивших машин не удовлетворяют стандартам качества. Определим, чему равна вероятность того, что хотя бы одна из 5 проверяемых машин будет забракована.
Решение. Здесь имеет место выборка без возвращения, следовательно, случайная величина – число бракованных автомобилей – подчиняется гипергеометрическому распределению: N = 10, К = 2, N–К = 8 и n = 5, т = 1, 2.
10


Р10,1 = C21C84/C105 = 0,5556,
2 5 8
Р10,2 = C22C83/C105 = 0,2222.
1 4
2 3
Р10,1+P10,2 = 0,5556 + 0,2222 = 0,7778.
Пример 4.12. На станцию под погрузку поступило 20 вагонов, среди которых один с дефектом. Из них случайным образом отобраны 2 вагона. Требуется:
1) построить закон распределения числа вагонов с дефектом;
2) построить биномиальное распределение, приняв в качестве постоянной вероятности р = 0,05, а числа испытаний – n = 2.
Решение:
1. По условию задачи N = 20, К = 1, п = 2. Случайная величина – число вагонов с дефектом т может принимать два значения; 0 и 1. По формуле (4.14) вычислим вероятности этих значений: P2,0 = C10C192/ /C202 = 0,9000; P2,1=C11C191/C201 = 0,1000. Полученные результаты сведем в табл. 4.9, что и будет гипергеометрическим законом распределения т.
Таблица 4.9
