
- •1. Основные понятия, определения и теоремы теории вероятностей*
- •1.1. Алгебра событий. Основые понятия теории множеств
- •1.2. Основные определения: испытание, событие. Классификация событий
- •1.3. Классическое определение вероятности. Свойства, вытекающие из этого определения
- •Значение вероятности
- •1.4. Основные теоремы теории вероятностей
- •1.5. Зависимые и независимые события
- •2. Формула полной вероятности и формула Бейеса
- •2.1. Формула полной вероятности
- •3. Случайные величины
- •3.1. Дискретные случайные величины
- •Ряд распределения случайной величины X
- •3.4. Ожидаемое среднее значение дискретной случайной величины
- •Вычисление математического ожидания числа рекламных
- •3.5. Свойства математического ожидания случайной дискретной величины
- •Возможные исходы лотереи
- •3.6. Ожидаемое среднее значение функции случайной величины
- •Ряд распределения числа месячных продаж
- •К вычислению среднего ожидаемого значения
- •3.7. Дисперсия дискретной случайной величины
- •К вычислению дисперсии случайной величины
- •3.9. Дисперсия линейной функции случайной величины
- •4. Законы распределения дискретных случайных величин
- •Формула Бернулли. Биномиальные вероятности
- •4.3. Биномиальный закон распределения
- •Биномиальное распределение
- •Биномиальное распределение X – числа гербов, появляющихся
- •Фрагмент таблиц ряда и функции биномиального распределения
- •Биномиальное распределение числа покупателей
- •Распределения
- •4.5. Распределение Пуассона
- •Закон распределения Пуассона
- •Сравнение вероятностей, полученных по формулам Бернулли и Пуассона
- •4.6. Гипергеометрическое распределение
- •Гипергеометрический закон распределения
- •Биномиальный закон распределения
- •Гипергеометрическое распределение
- •4.7. Производящая функция
- •4.8. Мультиномиальное распределение
- •4.9. Геометрическое распределение
- •5. Непрерывные случайные величины
- •6. Законы распределения непрерывных случайных величин
- •7. Закон больших чисел
- •7.1. Принцип практической уверенности. Формулировка закона больших чисел
- •7.2. Неравенства Маркова и Чебышева
- •7.3. Теорема Чебышева (частный случай)
- •7.4. Теорема Бернулли
- •7.5. Теорема Пуассона
4.9. Геометрическое распределение
Рассмотрим биномиальный эксперимент с обычными условиями. Пусть вместо вычисления числа успехов в независимых испытаниях случайная величина определяет число испытаний до первого успеха. Такая случайная величина распределена по закону геометрического распределения. Вероятности геометрического распределения вычисляются по формуле
P(m) = pqm–1, (4.I8)
где т = 1, 2, 3, ...; p и q – биномиальные параметры. Математическое ожидание геометрического распределения
M(m)= 1/p, (4.19)
а дисперсия σ2 = D(m) = q/p2 . (4.20)
Например, число деталей, которые мы должны отобрать до того, как найдем первую дефектную деталь, есть случайная величина, распределенная по геометрическому закону. В чем здесь смысл математического ожидания? Если доля дефектных деталей равна 0, 1, то вполне логично, что в среднем мы будем иметь выборки, состоящие из 10 деталей до тех пор, пока не встретим дефектную деталь.
Пример 4.16. Исследования в некотором регионе показали, что пепси-кола занимает 33,2 % рынка безалкогольных напитков, а кока-кола 40,9 %. Исследователи рынка собираются провести новое исследование, чтобы проверить вкусы и предпочтения потребителей пепси-колы. Потенциальные участники отбираются случайным образом среди потребителей безалкогольных напитков. Определим вероятность того, что случайно отобранный потребитель пьет пепси-колу. Рассчитаем вероятность того, что среди (двух, трех, четырех) отобранных потребителей безалкогольных напитков первым будет найден потребитель пепси-колы.
Решение. Пусть «успех» в единичном испытании с вероятностью 0,332 есть событие «первый случайно отобранный потребитель предпочитает пепси-колу». Используя геометрическое распределение при т=1, найдем из формулы (4.18): Р(1) = 0,332∙0,6880 = 0,332. Точно так же первый выбранный человек не будет, а второй будет потребителем пепси-колы с вероятностью P(2) = 0,332∙0,6881 = 0,2218. Вероятность того, что двое потребителей, не употребляющих пепси-колу, будут проинтервьюированы до того, как первый потребитель пепси-колы будет найден, равна P(3) = 0,332∙0,6882 = 0,1481. И окончательно P(4) = 0,332∙0.6883 = 0,099.
5. Непрерывные случайные величины
5.1. Определение непрерывной случайной величины. Функция распределения непрерывной случайной
величины
Непрерывной случайной величиной называют случайную величину, которая может принимать любые значения на числовом интервале.
Примеры непрерывных случайных величин: возраст студентов, длина ступни ноги человека, масса детали и т. д. Это положение относится ко всем случайным величинам, измеряемым на непрерывной шкале, таким как меры веса, длины, времени, температуры, расстояния. Измерение может быть проведено с точностью до какого-нибудь десятичного знака, но случайная величина – теоретически непрерывная величина. В экономическом анализе находят широкое применение относительные величины, различные индексы экономического состояния, которые также вычисляются с определенной точностью, скажем, до двух знаков после запятой, хотя теоретически их значения – непрерывные случайные величины.
У непрерывной случайной величины возможные значения заполняют некоторый интервал (или сегмент) с конечными или бесконечными границами.
Закон распределения непрерывной случайной величины можно задать в виде интегральной функции распределения, являющейся наиболее общей формой задания закона распределения случайной величины, а также в виде дифференциальной функции (плотности распределения вероятностей), которая используется для описания распределения вероятностей только непрерывной случайной величины.
Функция распределения (или интегральная функция) F(x) – универсальная форма задания закона распределения случайной величины. Для непрерывной случайной величины функция распределения также определяет вероятность того, что случайная величина X примет значение, меньшее фиксированного действительного числа х, т. е.
F(x) = F(X < x). (5.1)
При изменении х меняются вероятности Р(Х < x) = F(x). Поэтому F(x) и рассматривают как функцию переменной величины. Принято считать, что случайная величина X известна, если известна ее функция распределения F(x).
Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференци-руемая функция с непрерывной производной.
5.2. Свойства функции распределения
(для дискретных и непрерывных
случайных величин)
1. Функция распределения есть неотрицательная функция, заключенная между 0 и 1, т.е. 0 ≤ F(x) ≤ 1.
2. Функция распределения есть неубывающая функция, т. е. F(x2) ≥ F(x1), если х2 > х1. Тогда P(x1 ≤ Х < х2) = P(Х < х2) – P(Х < х1) = F(x2) – – F(x1).
Так как любая вероятность есть число неотрицательное, то P(x1 ≤ ≤ Х < х2) 0, а следовательно, F(x2) – F(x1) ≥ 0 и F(x2) ≥ F(x1).
Следствие 1. Вероятность того, что случайная величина X примет значение, заключенное в интервале (α, β), равна приращению функции распределения на этом интервале, т. е.
P(α ≤ Х < β) = F(β) – F(α). (5.2)
Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.
Р(Х = х1) = 0. (5.3)
Согласно сказанному, равенство нулю вероятности Р(Х = х1) не всегда означает, что событие Х = х1 невозможно. Говоря о вероятности события Х = х1, априорно пытаются угадать, какое значение примет случайная величина в опыте.
Если х1 лежит в области возможных значений непрерывной случайной величины X, то с некоторой уверенностью можно предсказать область, в которую случайная величина может попасть. В то же время невозможно хотя бы с малейшей степенью уверенности угадать, какое конкретное значение из бесконечного числа возможных примет непрерывная случайная величина.
Например, если метеослужба объявляет, что температура воздуха в полдень составила 5 °С, то это не означает, что температура будет точно равна этому значению. Вероятность такого события равна нулю.
3. Если все возможные значения случайной величины принадлежат интервалу (α, β), то
F(х) = 0 при х ≤ α; F(х) = 1 при х > β. (5.4)
В самом деле, F(x) = 0 для всех значений х ≤ α и F(х) = 1 при х > β, поскольку события X < х для любого значения х ≤ α, являются в этом случае невозможными, а для любого значения х > β – достоверными.
Следствие. Если возможные значения непрерывной случайной личины расположены на всей оси ОХ, то справедливы следующие предельные соотношения:
![]()
![]() ,
(5.5)
,
(5.5)
или F(– ∞) = 0; F(+ ∞) = 1. Это следствие справедливо и для дискретных случайных величин.
5.3. График функции распределения
для непрерывной случайной величины
Из перечисленных выше свойств F(х) может быть представлен график функции распределения (рис. 5.1).
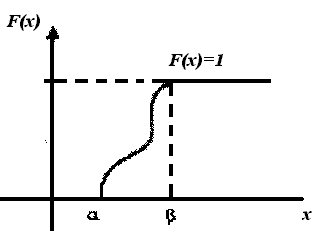
Рис. 5.1. График функции распределения
непрерывной случайной величины
График функции распределения смешанной случайной величины – кусочно-непрерывная функция (рис. 5.2).
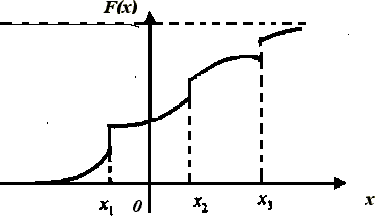

Рис. 5.2. График кусочно-непрерывной
функции распределения
5.4. Плотность распределения вероятностей непрерывной случайной величины
(дифференциальная функция)
Плотностью распределения вероятностей непрерывной случайной величины X называется функция W(x), равная первой производной от функции распределения F(x),
W(x) = F ′(x), (5.6)
где W(x) – дифференциальная функция распределения. Дифференциальная функция применяется только для описания распределения вероятностей непрерывных случайных величин.
5.5. Вероятность попадания непрерывной случайной величины в заданный интервал
Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (α, β), равна определенному интегралу от дифференциальной функции, взятому в пределах от α до β,
P(α
< X
<
β)
=
 .
(5.7)
.
(5.7)
Используя соотношения (5.2) и (5.1), получим P(α ≤ X < β) = P(α < < X < < β) = .
Геометрически этот результат равен площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения W(x) и прямыми х = α, х = β.
5.6. Нахождение функции распределения
по известной плотности распределения
Зная плотность распределения W(x), можно найти функцию распределения F(x) по формуле
F(x)
=
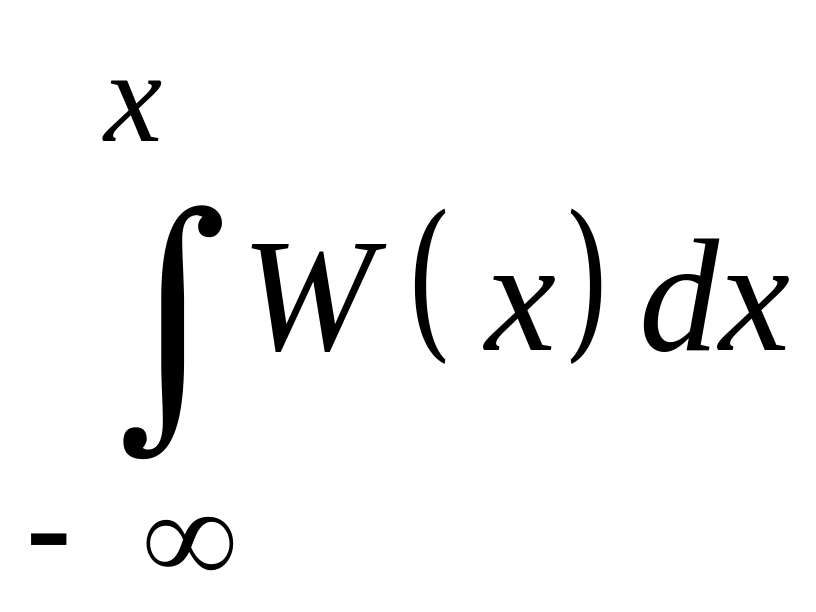 .
(5.8)
.
(5.8)
В самом деле, так как неравенство X < х можно записать в виде двойного неравенства – ∞ < X < х, то F(x) = P(– ∞ < X < х) = (рис. 5.3).


Рис. 5.3. Связь функции распределения с плотностью
распределения вероятностей
Таким образом, для полной характеристики непрерывной случайной величины достаточно задать функцию распределения или плотность ее вероятности.
5.7. Свойства дифференциальной функции распределения
1. Дифференциальная функция – неотрицательная функция:
W(x) ≥ 0. (5.9)
Это следует из того, что F(x) – неубывающая функция, а значит, ее производная неотрицательна.
2. Несобственный интеграл от дифференциальной функции в пределах от – ∞ до + ∞ равен 1
 .
(5.10)
.
(5.10)
Очевидно, что этот интеграл выражает вероятность достоверного события – ∞ < Х + ∞.
5.8. Числовые характеристики непрерывных случайных величин
Математическим ожиданием непрерывной случайной величины называется несобственный интеграл вида
М(Х)
= .
(5.11)
.
(5.11)
Дисперсией непрерывной случайной величины называется несобственный интеграл вида
D(x)
= σ2
= .
(5.12)
.
(5.12)
Средним квадратическим отклонением непрерывной случайной величины называется квадратный корень из дисперсии
σ
=
![]() .
(5.13)
.
(5.13)
Для числовых характеристик непрерывных случайных величин справедливы те же свойства, что и для дискретных. В частности, для дисперсии непрерывной случайной величины справедлива формула
D(X)=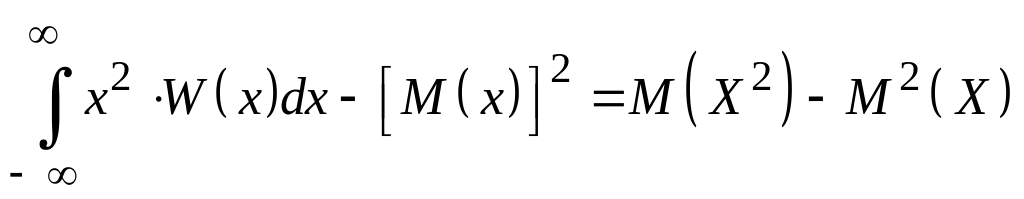 .
(5.14)
.
(5.14)
Начальным моментом k-го порядка (mk) случайной величины X называется математическое ожидание ее k-й степени:
для
дискретной случайной величины
mk= ;
;
для
непрерывной случайной величины
mk
=
 .
(5.15)
.
(5.15)
Центральным моментом k-го порядка (μк) случайной величины X называют математическое ожидание k-й степени отклонения случайной величины X от ее математического ожидания:
для
дискретной случайной величины
μk
= ;
;
для непрерывной случайной величины
μk
= .
(5.16)
.
(5.16)
Заметим, что начальный момент первого порядка m1 представляет собой математическое ожидание случайной величины, а центральный момент второго порядка μ2 – дисперсию случайной величины.
Центральный момент третьего порядка применяется для характеристики скошенности или асимметрии распределения (коэффициент асимметрии):
β1 = μ3/σ3. (5.17)
Для симметричных распределений β1 = 0. Центральный момент 4-го порядка применяется для характеристики крутости (эксцесса) распределения (неприведенный коэффициент эксцесса):
β2 = μ4/σ4. (5.18)
Часто в практических ситуациях используют квадрат коэффициента асимметрии и приведенный коэффициент эксцесса.
γ1 = β12 = μ23/σ6; γ2 = β2 –3 = μ4/σ4–3.
Величина хр, определяемая равенством F(xp) = Р(Х < хр), называется квантилью уровня p. Квантиль х0,5 называется медианой. Значение х, при котором W(x) принимает максимальное значение, называется модой.
