1. Основные понятия, определения и теоремы теории вероятностей*

В основу современной теории вероятностей легли результаты работ Б. Паскаля (1623–1662), П. де Ферма (1601–1665), Г. Галилея (1564–1642), Я. Бернулли (1654–1705), П. С. Лапласа (1749–1827), А. де Муавра (1667–1754) и других ученых. В XIX в. теория вероятностей сформировалась как стройная математическая дисциплина благодаря работам выдающегося русского ученого П. Л. Чебышева (1821–1894) и его учеников А. А. Маркова (1856–1922) и А. М. Ляпунова (1857–1918). В ХХ в. значительный вклад в развитие современной теории вероятностей внесли отечественные ученые: С.Н. Бернштейн, Б. В. Гнеденко, А. Н. Колмогоров, B. C. Пугачев, В. И. Романовский, Н. В. Смирнов, А. Я. Хинчин и др. Широкую известность приобрели фундаментальные работы зарубежных ученых: Г. Крамера, Д. Неймана, Р. Фишера, М. Кендалла, А. Стьюарта и др. Остановимся на основных понятиях теории вероятностей.

Теория вероятностей – раздел математики, изучающий случайные величины и их распределения.

Вероятность – количественная мера неопределенности, число, которое выражает степень уверенности в наступлении того или иного события.

Вероятность – число Р(А)Є[0;1], характеризующее степень возможности появления определенного события А.

Теория вероятностей – обязательный инструмент анализа ситуаций, включающих неопределенность.

Основная задача теории вероятностей – установление математических законов для исследования случайных явлений массового характера и предвидения их на основании отдельных фактов. В окружающем нас мире мы имеем дело с различными случайными явлениями, большое число которых подчиняется определенным закономерностям, проявляющимся только при большом числе наблюдений.

Теория вероятностей формирует основу для статистического вывода, а также для количественной оценки наступления или ненаступления некоторых событий, включая контроль качества, принятие управленческих решений, в инженерных расчетах в экономике и пр.

1.1. Алгебра событий. Основые понятия теории множеств

Математическим описанием связей между событиями занимается алгебра событий. Алгебру событий называют алгеброй Буля по имени английского математика Дж. Буля (1815–1864).

Для того чтобы понять смысл вероятности, напомним некоторые понятия теории множеств и операции над множествами.

Множество – это совокупность, набор, коллекция, собрание каких-либо элементов, объединенных по определенному признаку. Число элементов в множестве может быть конечным и бесконечным (например, все числа, лежащие между 0 и 1).

Полное множество Х – набор, содержащий все элементы в заданном контексте.

Пустое множество Ø – набор, не содержащий элементов. Всякое подмножество X есть множество (например, множество А, Ā и Ø). Задав набор А, можно определить его дополнение. Дополнением Ā множества А является набор, содержащий все элементы из полного набора X, которые не являются элементами набора А.

Диаграммы Венна, названные по имени английского логика Дж. Венна, наглядно представляют операции множеств и связанные с ними соотношения. На диаграммах Венна множество обозначается кругом, эллипсом или другой геометрической фигурой внутри прямоугольника, обозначающего полное множество.

Взаимоотношение между набором А и его дополнением показано на рис. 1.1, а.

Пример 1.1. Пусть полный набор – все студенты института. Определим А – множество студентов, сдавших летнюю сессию только на «отлично». Дополнение А есть – множество студентов неотличников. В сумме А и – все студенты института.

Рассмотрим подмножества А и В внутри полного множества X. Определим пересечение А и В.

Пересечение А и В (обозначается как А∩В) есть набор, содержащий все элементы, которые являются членами и А и В (см. рис. 1.1, б).

Объединение А и В (обозначается А В) есть набор, содержащий все элементы, которые являются членами или А, или В, или А и В вместе (см. рис. 1.1, в).

Продолжим рассмотрение примера со студентами. Определим В как множество студентов, сдавших зимнюю сессию на «отлично». Тогда пересечение А и В – подмножество студентов, сдавших на «отлично» и летнюю, и зимнюю сессии.

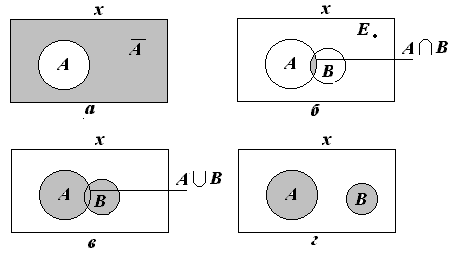
Рис. 1.1. Диаграммы Венна

Объединение А и В – подмножество студентов, которые сдали на «отлично» или летнюю, или зимнюю, или обе сессии.

Два набора могут не иметь пересечения. В этом случае мы говорим, что пересечение А и В есть пустое множество (см. рис. 1.1, г). В примере с успеваемостью студентов подмножество студентов, получивших двойки в летнюю сессию, не пересекается с подмножеством отличников.