3. Расчёт электрического состояния цепи с последовательным соединением элементов l, r, c.

Рассмотрим цепь из трех последовательных токоприемников (рис. 2.12 а): пер­вые два имеют активно-индуктивный характер, третий является последователь­ным соединением резистора и конденсатора. Проведем анализ цепи по векторной диаграмме. Произвольно строим вектор тока, который является базовым для всех векторов диаграммы. В соответствии со вторым законом Кирхгофа

,

где ; ; .

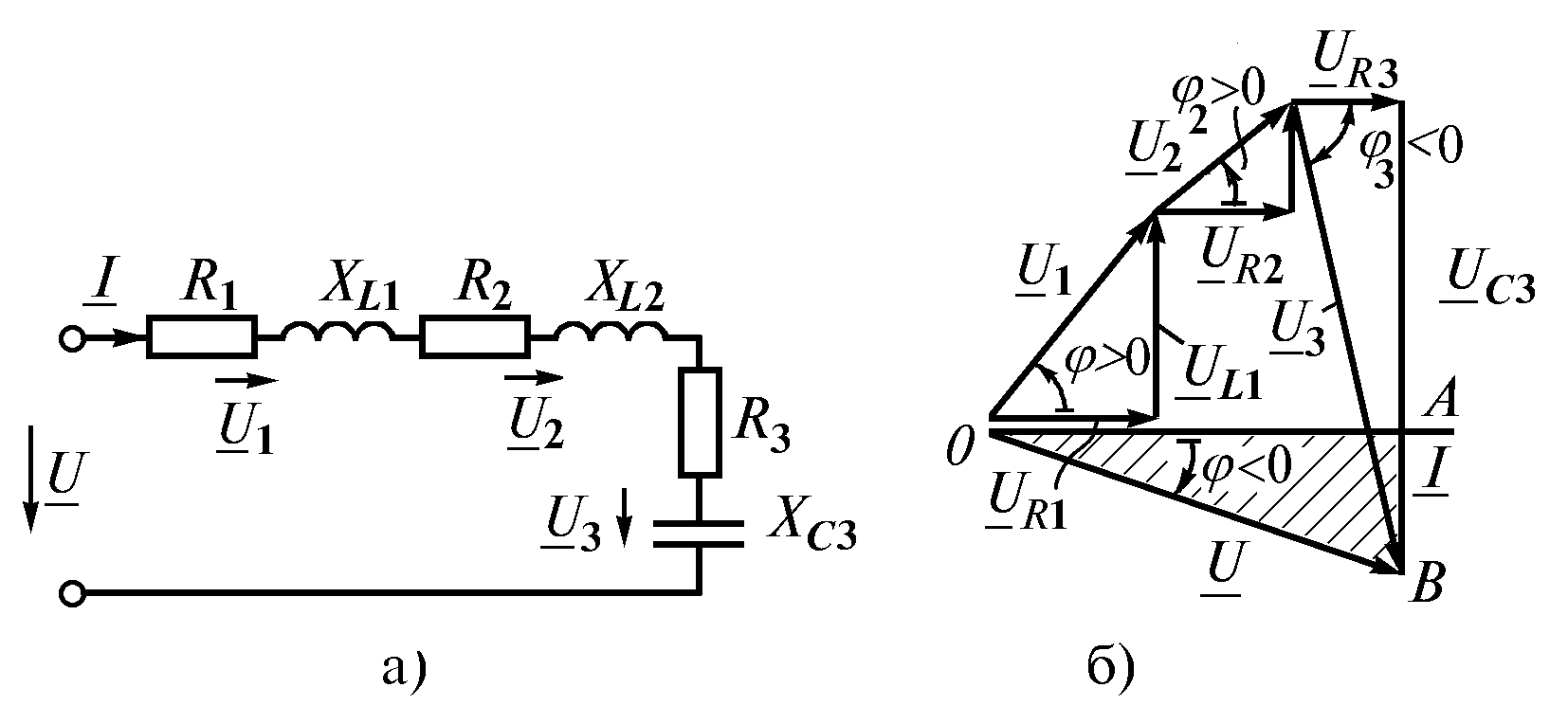
Рис. 2.12

Строим составляющие векторы, модули которых определяются по закону Ома. Суммарный вектор строим по правилу многоугольника. Векторы напряжений на активных сопротивлениях цепи совпадают по фазе с вектором тока, векторы опережают вектор тока на 90°, а вектор отстает от него на угол 90° (рис. 2.12 б). Действующее значение напряжения источника (модуль вектора ) по диаграмме находится из треугольника напряжений ОАВ

. (2.27)

В формуле (2.27) – активное сопротивление цепи, равное арифметической сумме сопротивлений последовательно включенных резисторов. В общем случае для последовательных приемников

.

является реактивным сопротивлением цепи, рав­ным алгебраической сумме реактивных сопротивлений последовательно вклю­ченных элементов. В общем случае

.

В приведенной схеме сумма векторов индуктивных напряжений меньше век­тора напряжения на конденсаторе, поэтому < 0. В таком случае говорят, что реактивное сопротивление (или цепь в целом) носит емкостный характер.

Для проверки проводим расчёт активной и реактивной мощности и полной мощности P, Q и S:

U=UI

4. Расчёт цепи с параллельным соединением r, l, c элементов

Рис. 2.13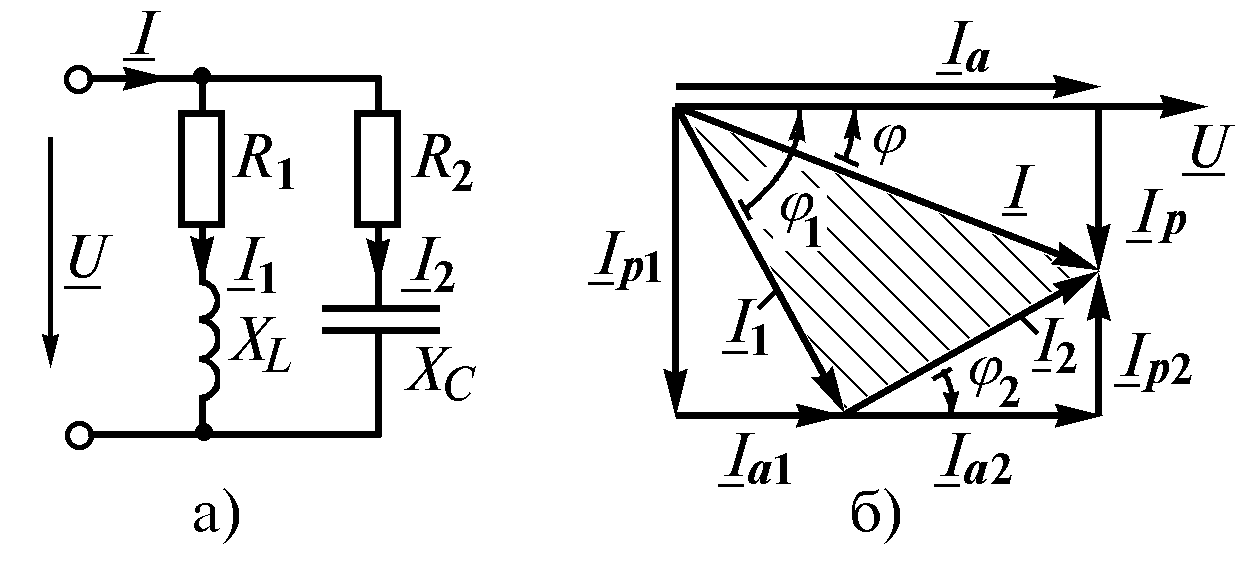

Рассмотрим цепь из двух параллельных ветвей (рис. 2.13 а). Допустим, что из­вестны напряже­ние источника и параметры схемы. Нужно определить ток , потребляемый от источника, и угол сдвига  на входе цепи. Для получения расчетных соотноше­ний построим векторную диаграмму токов. Предварительно рассчитаем токи в па­раллельных ветвях и углы их сдвига относительно приложенного напряжения. У первой ветви характер нагрузки индуктивный, ток отстает от на угол

; ; .

У второй ветви характер нагрузки емкостный, вектор опережает на угол

; ; .

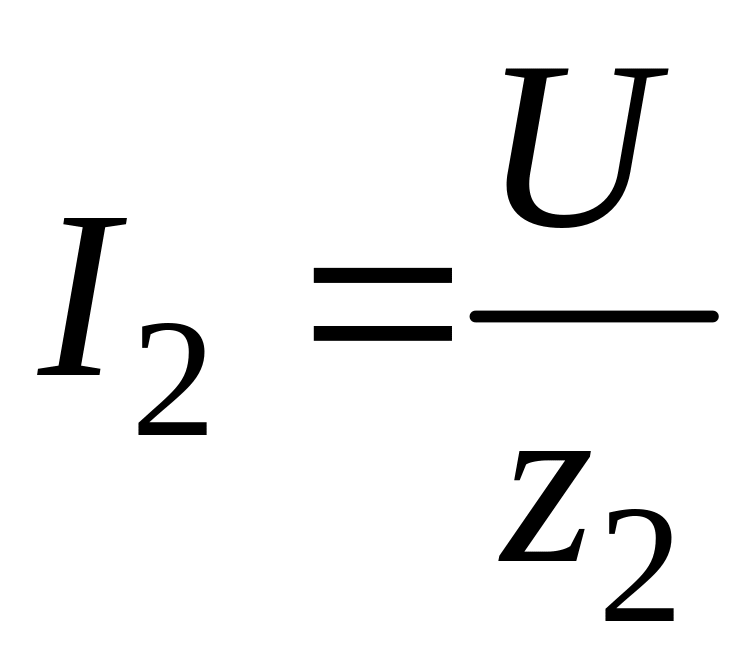В качестве основного вектора принимаем вектор напряжения источника , являющегося общим для двух параллельных ветвей (рис. 2.13 б). Тогда относи­тельно него нетрудно сориентировать векторы токов .

При выборе направления тока второй ветви угол откладываем от вектора в направ­лении, параллельном вектору , поскольку начала этих векторов не совме­щены. В соответствии с первым законом Кирхгофа ( ) определяем входной ток. В дальнейшем все расчетные соотношения получим из векторной диаграммы. Для этого представим каждый вектор проекциями на взаимноперпендикулярные оси. Проекцию вектора тока на вектор напряжения назовем активной составляющей тока , а перпендикулярную проекцию – реактив­ной составляющей . На диаграмме (рис. 2.13 б) эти составляющие показаны для всех векторов. Составляющие токи и физически не существуют и должны рас­сматриваться только как расчетные. По диаграмме активная составляющая вход­ного тока определяется как сумма активных составляющих токов в параллельных ветвях

(2.28)

где – активная проводимость цепи, равная арифметической сумме активных про­водимостей отдельных ветвей

где – активная проводимость -й ветви.

Только в частном случае, когда ветвь представляет собой чисто активное со­противление .

Реактивная составляющая входного тока определяется как алгебраическая сумма реактивных составляющих токов в параллельных ветвях. Реактивную со­ставляющую ветви с катушкой считают положительной, а с конденсатором – отри­цательной. Знаки учитывают при подстановке соответствующих значений

(2.29)

где – реактивная составляющая проводимости цепи, равная алгебраиче­ской сумме реактивных проводимостей отдельных ветвей.

В общем случае

где – реактивная проводимость отдельной -й ветви,

. (2.30)

Если рассматриваемая ветвь чисто реактивная: , проводимость является обратной реактивному сопротивлению. Ток на входе цепи (см. вектор­ную диаграмму на рис. 2.13 б) с учетом (2.28, 2.29)

(2.31)

где – полная проводимость цепи, равная геометрической сумме актив­ной и реактивной проводимостей.

Угол сдвига фаз также определяется из векторной диаграммы. На рис. 2.14 а изображена векторная диаграмма входного тока , его составляющих и и напряжения источника . Треугольник, образованный вектором тока и его проекциями , и , называется треугольником токов (рис. 2.14 а). Если сто­роны этого треугольника разделить на напряжение , получится треугольник, по­добный треугольнику токов – треугольник проводимостей. Он образован проводимостями , модули которых равны соответствующим проводимо­стям, а стороны совпадают с векторами , , треугольника токов (рис. 2.14 б).

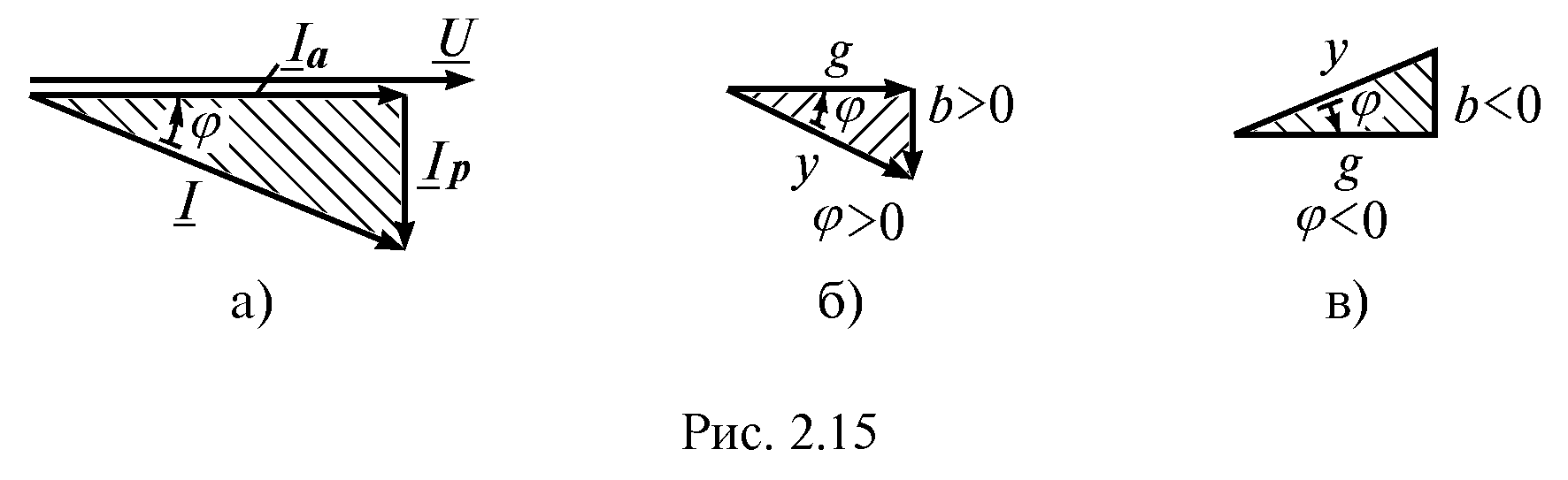
а) б) в)

Рис. 2.14

На рис. 2.14 в показан треугольник проводимостей при <0. Из него нахо­дим соотношения между параметрами и формулы для определения угла сдвига фаз

; ; ; ; ; . (2.32)

Чтобы учесть знак , следует использовать формулы тангенса и синуса.

В этой цепи, когда общий ток совпа­дает по фазе с напряжением, а входная реактивная проводимость или , может возникнуть явление резонанса. При противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в такой цепи получил название резонанса токов.

Пример Определить действующее значение входного тока по извест­ным токам в параллельных ветвях (риc. 2.15 а) = 3 A; = 1 A; = 5 A.

Решение находим по первому закону Кирхгофа

,

в соответствии с которым строим векторную диаграмму.

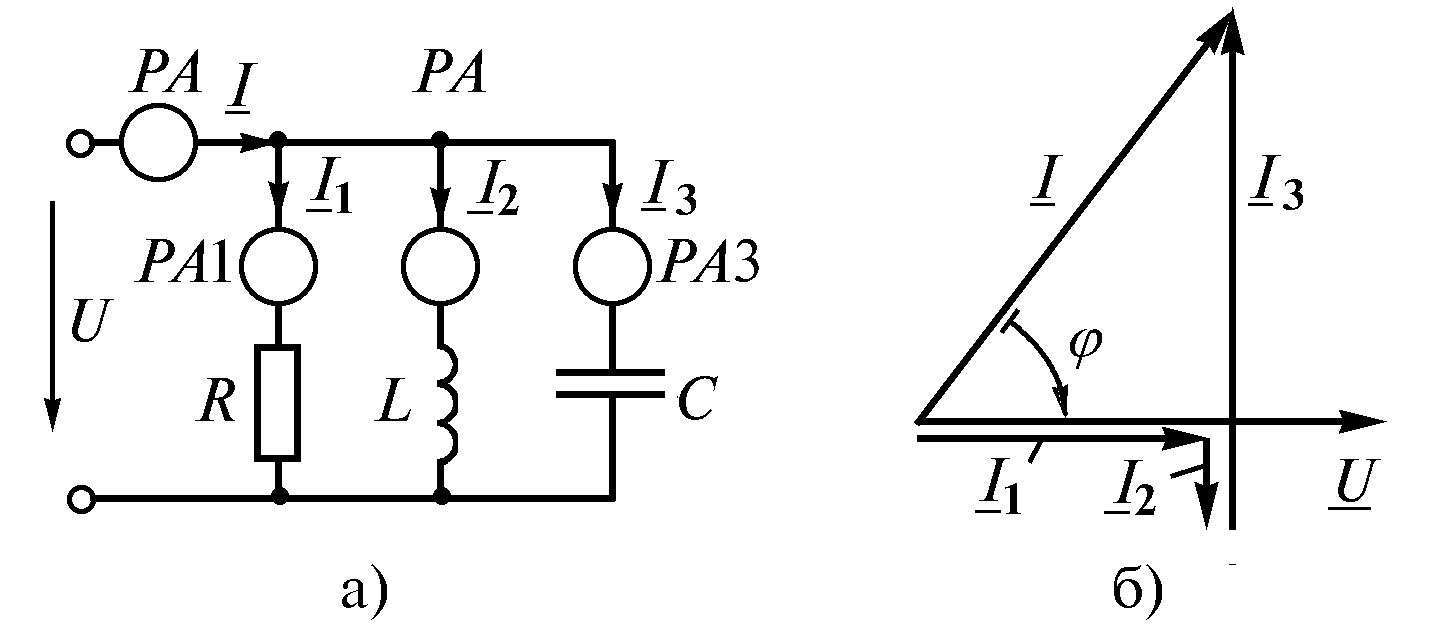
Рис. 2.15

Направления трех слагаемых тока выбраны по отношению к вектору . Из диаграммы (рис. 2.16 б) определяем ток

А.