
Системы обыкновенных дифференциальных уравнений
.pdf
|
|
|
|
|
|
|
|
Y = ϕ( x ), |
x a, b . |
|
|
Так как левая часть (9) тождественно равна нулю в (D), то она равна нулю и на |
|||||||||||
взятом решении, т.е. |
|
|
|
|
|||||||
|
|
∂u(x,ϕ( x)) |
+ |
∂u(x,ϕ(x)) |
F (x,ϕ( x))≡ 0, x a, b . |
||||||
|
|
|
|
|
|
||||||
|
|
|
∂x |
∂Y |
|
|
|||||
Так как Y = ϕ( x ) , x a, b , – решение системы (1) в (D), то F (x,ϕ( x))≡ ϕ′(x) , |
|||||||||||
x a, b . Следовательно, будем иметь |
|
|
|||||||||
|
|
|
∂u(x,ϕ( x)) |
+ |
∂u(x,ϕ(x)) |
ϕ′( x) ≡ 0, x a, b |
|
||||
|
|
|
|
|
∂Y |
||||||
|
|
|
∂x |
|
|
||||||
|
du(x,ϕ( x)) |
≡ 0, |
x a, b u(x,ϕ( x))≡ C, |
x a, b . |
|||||||
|
|||||||||||
|
|
|
dx |
|
|
|
|
||||
Последнее означает, что u( x,Y ) – интеграл системы (1) в (D).
Замечание. Допустим, что для системы (1) удалось построить в (D) n интегралов. Тогда можно построить вектор-функцию
u1(x,Y )
U( x,Y ) = u2 (x,Y )
. . .un ( x,Y )
и образовать соотношение U( x,Y ) = C .
Вопрос: Будет ли соотношение U( x,Y ) = C общим интегралом системы (1) в (D)?
Ответ: Не всегда.
4°. Понятие независимости интегралов. Пусть u1(x,Y ) , u2 ( x,Y ), ... , uk ( x,Y ) , k >1 – интегралы системы (1) в (D). Составим векторный интеграл
u1( x,Y )
U[k ]( x,Y ) = u2 (x,Y ) .
. . . uk (x,Y )
Составим матрицу Якоби для этого векторного интеграла
|
∂u1 |
∂u1 ∂u1 |
K |
∂u1 |
|
||||
|
|
∂x |
∂y |
|
|
|
|
|
|
|
∂y |
2 |
∂y |
n |
|||||
|
|
|
1 |
|
|
|
|
||
∂U[k ] |
|
∂u2 ∂u2 |
∂u2 |
K |
∂u2 |
|
|||
|
= |
∂x |
∂y |
∂y |
|
|
∂y |
|
. |
∂(x,Y ) |
2 |
|
n |
||||||
|
|
1 |
|
|
|
|
|||
|
|
K K K K K |
|
||||||
|
∂u |
∂u |
∂u |
K |
∂u |
||||
|
|
k |
k |
|
k |
|
k |
|
|
|
|
∂x |
∂y1 |
∂y2 |
|
∂yn |
|
||
21

Определение. Интегралы u1(x,Y ) , u2 ( x,Y ), ... , uk ( x,Y ) системы (1) в (D)
называются независимыми, если для любой точки (x,Y ) (D)
|
|
|
|
|
|
|
|
|
rang |
|
∂U[k ] |
|
|
|
|
= k . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
∂( x,Y ) |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Справедливо утверждение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пусть функции u1( x,Y ) , |
u2 (x,Y ), ... , uk ( x,Y ) являются интегралами систе- |
|||||||||||||||||||||||||||
мы (1) в (D). Тогда rang |
|
∂U[k ] |
= rang |
∂U[k ] |
, (x,Y ) |
(D), где |
|||||||||||||||||||||||
∂( x,Y ) |
|
∂Y |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
∂u1 |
|
|
∂u1 |
K |
∂u1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
2 |
|
∂y |
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
∂U |
[k ] |
|
|
∂u2 |
|
|
∂u2 |
K |
∂u2 |
|
||||||||||||
|
|
|
|
|
|
|
∂Y |
= |
∂y |
|
|
|
∂y |
|
|
|
|
|
∂y |
n |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
K K K K |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
∂u |
K |
∂u |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
k |
|
k |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
∂y1 |
|
|
∂y2 |
|
∂yn |
|
||||||||||||
|
|
По условию функции ui (x,Y ) |
|
( i = |
|
) являются интегралами системы (1) |
|||||||||||||||||||||||
|
|
1, k |
|||||||||||||||||||||||||||
в (D). Но тогда справедливы тождества: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
∂ui( x,Y ) + |
∂ui(x,Y ) |
F(x,Y ) ≡ 0 в (D) ( i = |
|
) |
||||||||||||||||||||||
|
|
|
1, k |
||||||||||||||||||||||||||
|
|
|
∂x |
|
|
∂Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∂ui( x,Y ) |
|
n |
∂ui( x,Y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= − |
∑ |
f j (x,Y ) , |
для любой точки (x,Y ) (D) ( i =1, k ). |
||||||||||||||||||||||||
|
∂x |
∂y |
j |
||||||||||||||||||||||||||
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возьмем произвольную точку (x,Y ) (D) и закрепим ее. Предыдущее соотно-
шение означает, что в закрепленной точке первый столбец матрицы |
∂U[k ] |
яв- |
|
∂(x,Y ) |
|||
|
|
||
ляется линейной комбинацией остальных ее столбцов (числа |
− f1(x,Y ) , |
||
− f2 ( x,Y ) , ... , − fn (x,Y ) выступают в качестве коэффициентов). Из этого и сле-
дует справедливость утверждения. 
Следствие. Система (1) имеет в области (D) не более чем n независимых интегралов.
 Это следует из того, что
Это следует из того, что
22

|
|
|
∂u1 ∂u1 |
K |
∂u1 |
|
|
|||
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
∂y |
2 |
∂y |
n |
|
||||
|
|
|
1 |
|
|
|
|
|
||
rang |
∂U[k ] |
|
∂u2 |
∂u2 |
K |
∂u2 |
|
≤ n , при любом k. |
||
∂Y |
= rang |
∂y |
∂y |
2 |
|
∂y |
n |
|
||
|
|
1 |
|
|
|
|
|
|||
|
K K K K |
|
||||||||
|
|
|
∂u |
∂u |
K |
∂u |
|
|
||
|
|
|
k |
∂y |
k |
|
k |
|
|
|
|
|
|
∂y1 |
|
|
∂yn |
|
|
||
|
|
144424443 |
|
|||||||
|
|
k |
строк; n столбцов |
|
||||||
5°. Достаточный признак общего интеграла.
Теорема. Пусть u1(x,Y ) , u2 ( x,Y ), ... , un ( x,Y ) – интегралы системы (1) в
u1(x,Y )
(D). Пусть U( x,Y ) = u2 (x,Y ) . Тогда если интегралы u1(x,Y ) , u2 ( x,Y ), ... ,
. . . un ( x,Y )
un ( x,Y ) – независимые в (D), то соотношение |
|
U( x,Y ) = C |
(11) |
есть общий интеграл системы (1) в (D).
 Покажем, что соотношение (11) удовлетворяет определению общего интеграла. Для этого берем произвольную точку (x0 ,Y0 ) ( D) и рассматриваем век-
Покажем, что соотношение (11) удовлетворяет определению общего интеграла. Для этого берем произвольную точку (x0 ,Y0 ) ( D) и рассматриваем век-
торное уравнение
U( x,Y ) =U( x0 ,Y0 ).
Перепишем (12) в виде
U ( x,Y ) −U (x ,Y ) = 0 .
144424440 30
=G( x,Y ) (обозначение)
(12)
(13)
Имеем:
1)G(x,Y ) C1(D) (так как U( x,Y ) C1( D)).
2)G(x0 ,Y0 ) = 0 ;
3) |
det |
∂G |
|
|
|
= det |
∂U |
|
|
≠ 0 (так как интегралы ui(x,Y ), i = |
|
– не- |
|
|
|
|
|||||||||
|
|
|
|
|
1, n |
|||||||
|
|
∂Y |
|
( x |
,Y ) |
|
∂Y |
|
( x |
,Y ) |
||
|
|
0 |
0 |
|
0 |
0 |
|
|
||||
зависимые в (D)).
Видим, что выполнены условия теоремы об однозначной разрешимости векторного уравнения (13) (см. теорию неявных функций). По этой теореме векторное уравнение (13) определяет единственную дифференцируемую век- тор-функцию
Y = ϕ( x ), x Iδ = ( x0 −δ, x0 +δ) ,
такую, что ϕ( x0 ) =Y0 .
Покажем, что вектор-функция Y = ϕ( x ) , x Iδ, является решением системы (1), по крайней мере, при достаточно малом δ ( δ > 0 ).
23

Так как вектор-функция Y = ϕ( x ) , x Iδ, – неявная, дифференцируемая
функция, определяемая уравнением (13), то она обращает (13) в тождество от- |
|||||||
носительно x на интервале Iδ , |
т.е. U(x,ϕ( x))−U(x0 ,Y0 ) ≡ 0 , x Iδ. Дифферен- |
||||||
цируя по x это тождество, получим |
|
|
|||||
|
∂U(x,ϕ( x)) |
+ |
|
∂U(x,ϕ(x)) |
ϕ′(x) ≡ 0, |
x Iδ . |
(14) |
|
|
|
|||||
|
∂x |
|
∂Y |
|
|
||
У нас U( x,Y ) – векторный интеграл системы в (D). Значит, каждая его компонента ui(x,Y ) ( i =1, n ) удовлетворяет в (D) тождеству
∂ui( x,Y ) + ∂ui(x,Y ) F(x,Y ) ≡ 0 .
∂x ∂Y
Эти n скалярных тождеств можно переписать в виде одного векторного тождества
|
∂U( x,Y ) |
+ ∂U(x,Y ) |
F(x,Y ) ≡ 0 в (D). |
|
||||
|
∂x |
∂Y |
|
|
|
|
|
|
Так как это тождество имеет место всюду в (D), то, в частности, оно выполня- |
||||||||
ется на линии Y = ϕ( x ) , x Iδ. Поэтому |
|
|
|
|
|
|||
|
∂U(x,ϕ( x)) |
+ |
∂U(x,ϕ(x)) |
F (x,ϕ( x))≡ |
0, |
x Iδ . |
(15) |
|
|
|
∂Y |
|
|||||
|
∂x |
|
|
|
|
|
||
Возьмем любое x Iδ и закрепим его. Рассмотрим при этом x линейную систему
|
∂U(x,ϕ( x)) |
|
∂U(x,ϕ(x)) |
|
|
z |
|
|
|
|
|
|
|
z1 |
|
|
|||
|
|
+ |
|
Z |
≡ 0 , где |
Z = 2 |
. |
(16) |
|
|
∂x |
∂Y |
|||||||
|
|
|
|
K |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂U(x,ϕ(x)) |
zn |
|
|
|
Определителем этой системы является det |
. Он отличен от нуля в |
||||||||
∂Y |
|||||||||
|
|
|
|
|
|
|
|
||
силу независимости интегралов u1( x,Y ) , u2 (x,Y ), ... , un ( x,Y ) . Следовательно,
система (16) имеет единственное решение. Но, как следует из (14) и (15), эта система имеет своими решениями векторы
Z = ϕ′( x ) и Z = F (x,ϕ(x)).
Так как система (16) имеет единственное решение, то получаем, что для взятого x Iδ
У нас x – любое, принадлежащее Iδ . Поэтому будем иметь ϕ′(x) ≡ F (x,ϕ(x)), x Iδ. Последнее означает, что Y = ϕ( x ) , x Iδ – решение системы (1).
Таким образом, показано, что соотношение (11) удовлетворяет определению общего интеграла системы (1) в (D).
24

Замечание 1. Чтобы составить общий интеграл системы (1) в (D), нужно найти n независимых интегралов этой системы.
Замечание 2. Пусть скалярная функция u(x,Y ) C1(D) – интеграл системы
(1) в (D), отличный от тривиального (т.е. u(x,Y ) ≡/ const в (D)). Соотношение u(x,Y ) = C называется первым интегралом системы (1) в (D). Отметим, что
u1(x,Y )
если U ( x,Y ) = u2 ( x,Y ) = C – общий интеграл системы (1) в (D), то
. . . un ( x,Y )
ui(x,Y ) = Ci ( i =1, n ) – первые интегралы системы (1) в (D).
§5. Методы интегрирования нормальных систем обыкновенных дифференциальных уравнений
1°. Метод исключения. Метод исключения является основным методом интегрирования нормальной системы. Он сводит задачу интегрирования данной системы к интегрированию одного или нескольких обыкновенных дифференциальных уравнений, каждое из которых представляет собой уравнение относительно одной неизвестной функции. Сущность метода состоит в следующем.
В системе
dy1 |
= f (x, y , y , K y ), |
|
||||||||
dx |
1 |
1 |
2 |
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
dy2 |
= f2 |
(x, y1, y2 |
, K yn ), |
|
||||||
|
(1) |
|||||||||
dx |
|
|
|
|
|
|
|
|
|
|
. . . . . . . . . |
|
|
|
|
||||||
dyn |
= f |
n |
( x, y |
, y |
2 |
, K y |
n |
) |
|
|
|
|
1 |
|
|
|
|
|
|||
dx |
|
|
|
|
|
|
|
|
|
|
берем какое-нибудь уравнение, например, первое, и дифференцируем его по x. Получим
y′′= |
∂f1 + |
∂f1 |
y′+ |
∂f1 |
y′ +K+ |
∂f1 |
|
y′ . |
|
|
|||
∂y |
|
|
|
|
|||||||||
1 |
∂x |
1 |
∂y |
2 |
2 |
∂y |
n |
|
n |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|||
Подставляя сюда значения y1′, y2′, K, |
yn′ |
из системы (1), будем иметь |
|||||||||||
y′′= ∂f1(x, y1, y2 , K, yn ) + |
∂f1(K) f (x, |
y , y |
2 |
, K, y |
n |
) + |
|||||||
1 |
∂x |
|
|
|
|
1 |
1 |
|
|
|
|
||
|
|
|
∂y1 |
|
|
|
|
|
|
|
|||
+ ∂f1(K) f2 (K) +K+ ∂f1(K) fn (K) , |
|
|
|||||||||||
|
∂y2 |
|
|
|
|
∂yn |
|
|
|
|
|
|
|
25
или |
|
y1′′= f11(x, y1, y2 , K, yn ) . |
(2) |
Полученное соотношение (2) тоже дифференцируем по x и подобным же образом, т.е. используя уравнения системы (1), приходим к уравнению
После (n −1) |
|
|
|
|
y1′′′= f12 (x, y1, y2 , K, yn ) . |
|
|
|
(3) |
||||||||||||||||||||||||||||||||
таких шагов мы придем к уравнению |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y( n) |
= f |
|
|
( x, y , y |
2 |
, K, y |
n |
) . |
|
|
(4) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1,n−1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рассмотрим теперь систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
y1′ = f1(x, y1, y2 , K yn ), |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
′′ = |
|
f ( x, y , y |
2 |
, K y |
n |
), |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
11 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
y |
′′′= |
|
f (x, y , y |
2 |
, K y |
n |
), |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
12 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
||||||
|
|
|
|
|
|
|
|
. . |
|
. . . . . . . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x, y , y |
|
, K y |
|
|
), |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
y( n−1)= f |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1,n− |
2 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
n |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
y( n) |
= f |
|
−1 |
( x, y , y |
2 |
, K y |
n |
). |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1,n |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Допустим, |
что из первых |
|
(n −1) |
|
|
уравнений системы |
(5) |
удается найти |
|||||||||||||||||||||||||||||||||
y |
2 |
, |
y |
3 |
, K, |
y |
n |
, т.е. выразить y |
2 |
, y |
3 |
, |
K, |
y |
n |
через x, y , |
y′, |
y′′, K, y( n−1) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
||||||
|
|
|
|
|
|
|
|
y |
|
|
= ϕ |
|
|
(x, |
y |
|
|
, y′, y′′, K, |
y( n−1) ), |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
y |
|
|
= |
ϕ |
|
(x, |
y |
|
, y′, |
y |
′′, K, |
y( n−1) ), |
|
|
(6) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
. . . . . . . . . . . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
n |
= |
ϕ |
n |
(x, y |
|
, |
y′, y′′, K, |
y( n−1) ). |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
Подставляя эти значения для |
|
|
y2 , |
|
y3, K, |
|
yn в последнее уравнение системы |
||||||||||||||||||||||||||||||||||
(5), будем иметь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
y( n) = f (x, y , y′, y′′, K, |
y( n−1) ) . |
|
|
(7) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
Получили, таким образом, одно дифференциальное уравнение n-го порядка относительно одной неизвестной функции. Интегрируя это уравнение, получим
y1 = Φ1( x, C1, C2 , K, Cn ) |
(8) |
(предполагается, что мы умеем находить общее решение уравнения (7)). |
|
Теперь, дифференцируя полученную функцию (8) |
последовательно (n −1) |
раз и подставляя значения y1, y1′, y1′′, K, y(1n−1) в (6), получим
y2 = Φ2 (x, C1, C2 , K, Cn ), y3 = Φ3(x, C1, C2 , K, Cn ),
. . . . . . . . .
yn = Φn (x, C1, C2 , K, Cn ),
26

которые вместе с ранее найденным y1 ( = Φ1( x, C1, C2 , K, Cn ) ) составляют об-
щее решение системы (1).
Замечание. В рассматриваемом случае процесс исключения можно вести и в ином порядке. Так, например, можно выражать y2 , y3, K, yn через
x, y , |
y′′, y′′′, K, |
y( n) из последних (n −1) |
|
уравнений системы (5) и подста- |
||||||||||||||||||||||
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вить в первое. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 1. Найти общее решение системы |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
dy1 |
= −3x −2 y +3y +4 y , |
|
|
|
|
||||||||||||||||||
|
|
|
dx |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
dy |
2 |
|
=1−7x −6 y1 + |
7 y2 +6 y3, |
|
||||||||||||||||||
|
|
|
|
|
|
|
(1 ) |
|||||||||||||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dy3 |
= x + y − y |
2 |
+ y |
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продифференцируем по x первое уравнение из системы (1 ) : |
|
|||||||||||||||||||||||||
|
|
|
|
y1′′= −3 −2 y1′ +3y2′ +4 y3′. |
|
~ |
|
|||||||||||||||||||
Подставляя здесь вместо y1′, y2′, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y3′ их выражения из (1 ) , получим |
~ |
|||||||||||||||||||||||||
|
|
|
y1′′= −11x −10 y1 +11y2 +14 y3 . |
|
|
|||||||||||||||||||||
|
|
|
|
|
( 2) |
|||||||||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученное уравнение ( 2) дифференцируем по x: |
|
|
|
|
|
~ |
||||||||||||||||||||
|
|
|
y1′′′= −11−10 y1′ +11y2′ |
|
+14 y3′. |
|
|
|||||||||||||||||||
|
|
|
|
|
~ |
( 3) |
||||||||||||||||||||
И здесь вместо y1′, |
y2′, y3′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
подставляем их выражения из (1 ) . Получим |
||||||||||||||||||||||||||
|
|
|
y′′′= −33x −32 y |
|
+33y |
|
|
|
+40 y |
|
. |
~ |
||||||||||||||
|
|
|
|
2 |
|
3 |
( 4) |
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассматриваем теперь систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y′ = −3x −2 y + |
3y |
|
+4 y |
, |
|
|
|
|
~ |
||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
y1′′= −11x −10 y1 +11y2 +14 y3, |
|
|
( 5) |
||||||||||||||||||||
|
|
|
y′′′= −33x −32 y |
|
|
+33y |
2 |
+ |
40 y |
|
. |
|
||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||
|
|
|
|
~ |
|
|
|
|
|
|
|
|
и y3 через x, y1, y1′, |
y1′′: |
||||||||||||
Из первых двух уравнений ( 5) выражаем y2 |
||||||||||||||||||||||||||
|
|
|
|
y |
2 |
= 2 y′′− |
7 y′ +6 y |
|
|
+ x, |
|
|
|
|
~ |
|||||||||||
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y |
3 |
= |
1 (−3y′′+11y |
′−8 y ). |
|
|
|
( 6) |
||||||||||||||
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
Подставляем найденные значения для |
y2 |
|
и |
y3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
в последнее уравнение ( 5) . По- |
|||||||||||||||||||||||
лучим |
|
|
|
y′′′− |
6 y′′+11y |
′ −6 y |
|
|
= 0 . |
|
|
|
~ |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
( 7 ) |
|||||||||||||||||
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
~
( 7) – линейное однородное уравнение с постоянными коэффициентами. Составляем характеристическое уравнение:
27

λ3 −6λ2 +11λ −6 = 0 λ1 =1, λ2 = 2, λ3 = 3 . |
|
|
|||||||||||||||||||
Следовательно, |
|
|
|
|
|
= C ex |
+C e2x +C e3x |
|
|
~ |
|||||||||||
|
|
|
y |
|
. |
|
|||||||||||||||
|
|
|
|
|
( 8 ) |
||||||||||||||||
|
|
|
~ |
1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
3 |
|
|
~ |
||
|
|
|
|
два раза и подставляя значения y1, y1′, |
y1′′ |
||||||||||||||||
Теперь, дифференцируя ( 8 ) |
|
в ( 6) , |
|||||||||||||||||||
получаем |
|
|
+C ex +3C e3x , |
|
|
|
|
|
|
|
= C e2x −C e3x . |
|
|
||||||||
y |
2 |
= x |
|
|
y |
3 |
|
|
|||||||||||||
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
2 |
3 |
|
|
||||
Совокупность функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
y |
|
= C ex +C e2x +C e3x , |
|
|
||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
y2 = x +C1e |
x |
+ |
3C3e |
3x |
, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
y |
|
|
= C e2x −C e3x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– общее решение системы (1 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 2. Найти общее решение системы |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
y′ |
= y |
|
+ y |
|
, |
|
|
|
|
~ |
||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
y2′ = y1 + y3, |
|
|
|
|
(10 ) |
|||||||||
|
|
|
|
|
|
|
y′ |
= y |
+ y |
2 |
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
~ |
|
|
||
Дифференцируя по x первое уравнение системы (10 ), получим |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
y1′′= y2′ + y3′. |
|
|
~ |
|
|
|
||||||||
Подставив здесь вместо y2′, y3′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
их выражения из (10 ), будем иметь |
|
~ |
|||||||||||||||||||
|
|
|
|
|
|
|
y1′′= 2 y1 +( y2 + y3 ) . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
( 20 ) |
||||||||||||
Замечаем, что уравнения
y1′ = ( y2 + y3 ),
y1′′= 2 y1 +( y2 + y3 )
содержат y2 и y3 “одинаковым образом” и, следовательно, из этих уравнений
они могут быть исключены сразу. В результате мы получим уравнение второго порядка для y1 :
~
y1′′− y1′ −2 y1 = 0 , ( 70 )
~
и в дальнейшем дифференцировании уравнения ( 20 ) надобности нет. Интегри-
~
руя уравнение ( 70 ) , получим
|
|
|
|
y |
= C e−x +C e2x . |
|
|
||||
|
|
|
|
1 |
|
1 |
2 |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
= y1′ − y2 и подставим |
||
Найдем теперь y3 из первого уравнения системы (10 ): y3 |
|||||||||||
во второе уравнение этой системы. Будем иметь: |
|
|
|
||||||||
y′ |
= y + y′ − y |
2 |
y′ |
= 3C e2x − y |
2 |
y′ + y |
2 |
= 3C e2x . |
|||
2 |
1 |
1 |
|
2 |
2 |
|
2 |
2 |
|||
28

Мы получили уравнение первого порядка для y2 . Решая его, находим: y2 = C2e2x +C3e−x . Остается найти y3 , для чего можно использовать, например,
~
второе уравнение системы (10 ):
y |
3 |
= y′ |
− y |
= 2C e2x −C e−x −C e−x −C e2x |
y |
3 |
= C e2x −(C +C ) e−x . |
|||||
|
2 |
1 |
2 |
3 |
1 |
2 |
|
2 |
1 |
3 |
||
Таким образом, в рассматриваемом случае нам пришлось интегрировать одно уравнение второго порядка и одно первого порядка. И вообще, следует отметить, что интегрирование нормальной системы порядка n методом исключения может свестись к интегрированию нескольких дифференциальных уравнений, сумма порядков которых равна n.
Рассмотрим случай, когда метод исключения приводит к интегрированию n уравнений первого порядка.
Пусть имеется система обыкновенных дифференциальных уравнений вида
|
dy1 |
|
|
= f ( x , y ), |
|
|
|
|
||||
|
|
|
|
|
||||||||
dx |
1 |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy2 |
|
= f ( x , y , y ), |
|
|
|||||||
|
|
|
||||||||||
dx |
|
|
2 |
1 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
3 |
|
|
= f3 |
( x , y1, y2 , y3 ), |
|
|
|||||
|
|
|
|
|
~ |
|||||||
|
|
|
|
|||||||||
dx |
|
|
|
|
|
|
|
|
( 1 ) |
|||
. . . . . . . . . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dyn |
= f |
n |
( x , y |
, y |
, K y |
n |
). |
||||
|
||||||||||||
dx |
|
|
1 |
|
2 |
|
|
|||||
|
|
|
~ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Интегрируя первое уравнение системы (1 ) , найдем |
||||||||||||
|
|
|
|
|
y1 = Φ1( x, C1 ) . |
|
~ |
|||||
Подставляя это выражение для |
|
|
|
|
|
|
|
|
||||
|
y1 во второе уравнение системы (1 ) , получим |
|||||||||||
уравнение первого порядка для y2 :
dydx2 = f2 (x, Φ1( x, C1 ), y2 ).
Интегрируя это уравнение, получим
y2 = Φ2 ( x, C1, C2 ) .
~
Подставляя в третье уравнение системы (1 ) вместо y1 и y2 соответственно Φ1( x, C1 ) и Φ2 ( x, C1, C2 ) , получим уравнение первого порядка для y3 :
dydx3 = f3(x, Φ1(x, C1 ), Φ2 (x, C1, C2 ), y3 ).
Проинтегрировав это уравнение, найдем
y3 = Φ3( x, C1, C2 , C3 ) , и т. д.
Наконец, придем к уравнению первого порядка для yn :
29
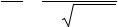
dydxn = fn (x, Φ1(x, C1 ), Φ2 (x, C1, C2 ), K, Φn−1( x, C1, C2 , K, Cn−1 ), yn ).
Проинтегрировав это уравнение, найдем
yn = Φn ( x, C1, C2 , C3, K, Cn −1, Cn ) .
Совокупность функций Φ1( x, C1 ) , Φ2 ( x, C1, C2 ) , ... , Φn ( x, C1, C2 , K, Cn ) являет-
~
ся общим решением системы (1 ) .
2°. Симметрическая форма нормальной системы. Нахождение интегри-
руемых комбинаций. Нормальную систему (1) можно записать в виде равенст-
ва отношений: |
|
|
|
|
|
|
dy2 |
|
|
|
|
|
dyn |
|
|
|
|
|
|||||||
|
|
dy1 |
|
|
= |
|
|
|
|
=K= |
|
|
|
|
= |
dx |
. (9) |
||||||||
|
f ( x, y , y |
2 |
, K, y |
n |
) |
f |
2 |
(x, y , y |
2 |
, K, y |
n |
) |
f |
n |
(x, y , y |
2 |
, K, y |
n |
) |
1 |
|||||
1 |
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||||||
Равенство отношений (9) называется симметрической формой нормальной системы (1). Такое название объясняется тем, что в (9) все переменные x, y1, y2 , K, yn равноправны: любую из них можно выбрать в качестве неза-
висимой. Последнее обстоятельство бывает иногда очень полезным в теории и практике интегрирования систем.
Мы видели, что задача построения общего решения нормальной системы порядка n равносильна нахождению n ее независимых интегралов. Общего способа построения интегралов не существует, но в отдельных случаях они могут быть сравнительно просто найдены. Для нахождения интегралов системы (9) либо берут пары отношений, допускающих разделение переменных, либо ис-
пользуют производные пропорции: |
|
|
|
|
|
|
|
|
|
|
|
|||
dx |
= ω0dx +ω1dy1 +ω2dy2 +K+ωndyn . |
(10) |
||||||||||||
1 |
ω |
0 |
+ω |
f |
1 |
+ω |
2 |
f |
2 |
+K+ω |
n |
f |
n |
|
|
|
1 |
|
|
|
|
|
|
||||||
Здесь ω0 (x, y1, y2 , K, yn ) , ω1( x, y1, y2 , K, |
yn ), ... , ωn (x, y1, y2 , K, yn ) – произ- |
|||||||||||||
вольные функции, и их выбирают так, чтобы числитель правой части был дифференциалом знаменателя, либо числитель был полным дифференциалом некоторой функции u( x, y1, y2 , K, yn ) , а знаменатель был равен нулю, т.е. чтобы
одновременно выполнялись два условия:
1.ω0 +ω1 f1 +ω2 f2 +K+ωn fn = 0 ;
2.ω0dx +ω1dy1 +ω2dy2 +K+ωndyn = du(x, y1, y2 , K, yn ) .
Если эти условия оказываются выполненными, то из (10) получается du = 0 ,
откуда видно, что функция u( x, y1, y2 , K, yn ) является интегралом данной
системы. |
|
|
|
|
Пример 3. Найти интегралы системы |
|
|
||
dx |
= dy |
= |
dz |
(11) |
xz |
yz |
xy |
z2 |
+1 |
 (11) – система двух дифференциальных уравнений относительно двух неизвестных функций, записанная в симметрическом виде. Области, в которых
(11) – система двух дифференциальных уравнений относительно двух неизвестных функций, записанная в симметрическом виде. Области, в которых
30
