Справочник по векторному анализу.

1. Векторное поле (функция ,принимающая векторные значения) (P,Q)(P(x,y),Q(x,y)) называется потенциальным, если существует скалярная функция U(x,y): (P,Q)=gradU, т.е.;

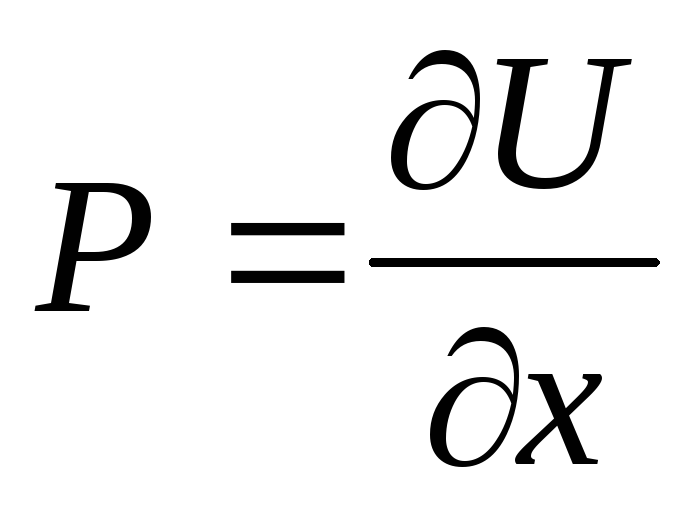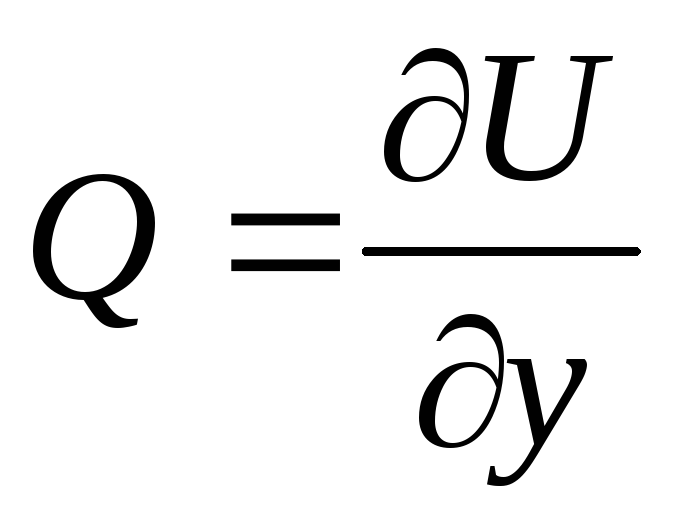
2. При этом U(x,y) называется потенциалом поля (P,Q).

3. Эквивалентные условия потенциальности поля:

а) Потенциальность

б) Потенциальностьне зависит от траектории (следует из формулы Грина)

4. При условиях потенциальности

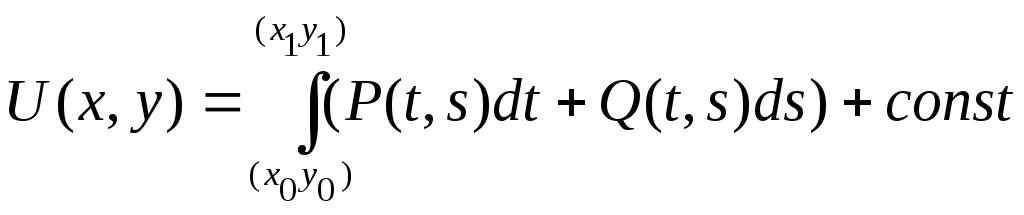
5. Pdx+Qdy - уравнение в полных дифференциалах Pdx+Qdy=dU => U(x,y) – общий интеграл ДУ, т.е. уравнение U(x,y)=const задает решение y(x).

Теорема: ₀(x,y) – интегральный множитель для Pdx+Qdy=0 (1)

₀(x,y) – некий общий интеграл для (1), тогда и другой интегрирующий множитель(x,y) задается формулой:(x,y)=₀(x,y)g(₀(x,y)), где g произвольная функция.

Теорема: 1 В конечномерных пространствах, множество , компактно <=> оно ограничено и замкнуто, а предкомпактность <=> ограниченности.

Следующие 2 теоремы верны в любом полном метрическом пространстве.

Теорема: 2 Хаусдорфа.

Множество предкомпактно <=>>0 существует конечное {x₁, x₂,…,x_n} :, т.е. множество {x_n} – это- сеть, это означаетxx_k: |x-x_k|<

Теорема: 3 Гейне-Бореля

Утв:

1. dist(A,B)=inf dist_xA(x,B)

2. f(x)=dist(x,A) непрерывнамножества А.

3. dist (A,B)=dist(A,B)

4. Для конечно мерных пространств: если A,B – замкнуты, и хотя бы 1 из них ограничено, то dist(A,B) достигается на некоторой паре элементов.

Следствие: Если множества А,B замкнуты, не пересекаются и хотя бы 1 ограничено, то dist(A,B)>0

5. Пусть - открыто, K – компакт, тогда dist(K,>0

6. Для любого множества dist(,_

Теорема: 1 Вейерштрасса. Функция, непрерывная на компакте, ограничена, причем min и max достигаются.

Теорема: 2 Кантора. Функция, непрерывная на компакте, равномерно непрерывна, т.е. выполняется соотношениеТ.е. существует функция

Теорема: О неявной функции.

Пусть 1) x,yRⁿxR^m, fR^mf имеет ту же размерность, что и y.

2) f непрерывно дифференцируема в RⁿxR^m

(x₀,y₀)

4) det(f_y') |_(x0,y0)0 (Матрица Якоби квадратная)

тогда

1. В некоторой окрестности x₀функция y=y(x) : f(x,y(x)=0, т.е.функция которая неявно задается таким уравнением

2. Такая функция единственна

3. y(x) – непрерывно дифференцируема причем y'_x=-(f_y')^-1f_x'

f_x' – производная неявной функции

Теорема: 2 об обратной функции

x_y^’=(y_x^’)^-1если det(y_x^’)0

Функция f удовлетворяет условию Липшица, если |f(x)-f(y)|<L|x-y|x,y : L - константа Липшица

Теорема: Принцип выбора Кантора

Пусть последовательность функций {f_n} равномерно ограничена на,

Пусть - это некоторое счетное подмножество, тогда существует подпоследовательность {f_n,k}, сходящаяся в()

Теорема: 2 Арцела – критерий компактности с C(

Пусть - компакт: множество MC()

Тогда множество M – предкомпактно, в C(), тогда и только тогда, когда функции из M равномерно ограничены и равностепенно непрерывны.

Замечание: Теорема Хаусдорфа в конечном по х случае, не нужна - сети можно строить деляпополамкоординате.

Теорема: Априорная оценка решений.

Предположим, что 1) y(t) – решение y'=f(t,y) (1a), определим на t[s,s+]

2) f(t,y) непрерывна и ограничена : |f(t,y)|<Mt,y

на пересечении области определения f и окрестности [s,s+]xN_z,

|y(t)-z|<t[s,s+]=min{,^/_M}

гарантируем не слишком большой рост y на некотором замкнутом интервале.

Теорема: Пикара

Пусть 1) =[ s,s+] xN_z,

2) f непрерывна и ограничена на : |f(t,y)|f(t,y)|<M(t,y)

3. f равномерно Липшицева по y на 

=min{,^/_M}, тогда задача (1a) на [s,s+] имеет единственное решение

Замечание:

1. Равномерно Липшицевость гарантируется, если равномерно ограниченная производная по y

2. Из теорема Пикара => что через 1 () области проходит ровно одна интегрирующая кривая, если правая часть непрерывно дифференцируем по y

3. Функция y_kназывается последовательным приближением Пикара и их можно использовать для построения приближенного решения.

4. На всем интервале [s,s+] решение может и не существовать.

Теорема: Пеано.

Предположим 1) =[s,s+] xN_z,

2) f непрерывна на и |f|<M

Обозначим =min{,^/_M}, тогда на [s,s+] существует решение.

Лемма: 1 (о продолжительности сходимости)

Предположим: 1) y(t) – решение ДУ : y'=f(t,y), определенные на [a,b)

2) Существует t_kb-0 : y(t_k)z

3) |f|<M, в некторой окрестности точки (b,z)

тогда y(t)ztb-0

Теорема: Пусть f(t,y) непрерывна по ограниченной области (открытой)

y(t) некоторое решение ДУ y'=f(t,y) тогда

1. Это решение может быть продолжено (как решение) на интервал (_-,₊) : dist((t,y(t)),)0 при t₊

2. Если кроме того |f(t,y)|<M,(t,y), то существует

Опр: Интервал (_-,₊) из теоремы называется предельным (максимальным) интервалом существования решения.

Замечание: Возможны 2 случая

1. Решение задачи Коши не единственное, тогда (_-,₊) определен не однозначно

2. Решение любой задачи Коши в единственное, тогда

1. (-,+) определен однозначно

2. Понятие максимального интервала можно обобщить на неограниченную область, для неограниченных областей можно положить (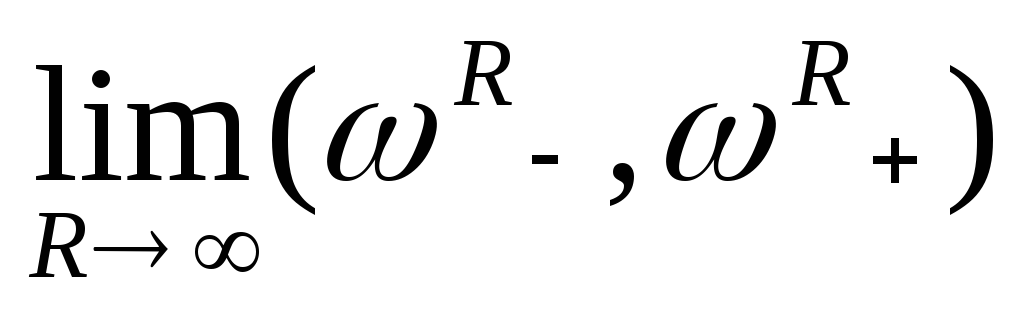-,+)=, где_^R=_для областиN_0,R

Следствие: Если решение любой задачи Коши единственное, то любое решение выходит за пределы любого компакта содержащегося в в том числе неограниченного.

т.е. Пусть K- компакт

Пусть (t₀,y₀)K, y(t) – решение с начальным значением (t₀,y₀), тогда существует t₁<t₀<t₂: (t₁,y(t₁))K и (t₂,y(t₂))K, т.к. K отделено отнекоторым расстоянием.

Теорема: Полунепрерывность интервала существования)

Предположим 1) f(t,y,p) непрерывна в области (существует)

2) через любую точку области проходит ровно 1 интегральная кривая (существует единственное)

3. [a,b](_-(s₀,z₀,p₀),₊(s₀,z₀,p₀)), где (s₀,z₀,p₀)

тогда существует ((s,z,p)N_{(s0,z0,p0),}), можно утверждать, что [a,b](_-(s₀,z₀,p₀),₊(s₀,z₀,p₀)), т.е. интервал существования не может скачком уменьшиться, хотя может скачком увеличиться.

Теорема: 2

Предположим 1) f непрерывна в области 

2. через любую точку области проходит ровно 1 интегральная кривая

Обозначим _={t,s,z,p : (s,z,p): t(_-(s₀,z₀,p₀),₊(s₀,z₀,p₀))} (множество на котором определено решение(t,s,z,p) – открытое множество

тогда 1) (t,s,z,p) непрыревно на_

2) Графики решений непрерывно зависят от своих параметров, т.е. (>0): ((t,s,z,p)N_{(t0,s0,t0,p0),}) график Г(t,s,z,p), попадет в-окрестность графика Г(t₀,s₀,z₀,p)

Дифференцируемость решения

Теорема: 1

Пусть f и непрерывна в области, тогда решение (1а)(t,s,z,p) непрерывна дифференцируема в_по совокупности ограничена.

Замечание: Пусть f(t,y,p) непрерывно дифференцируема по всем аргументам, тогда непрерывно дифференцируема, но только по t.

Теорема: 2 Пусть f(t,y,p) l раз непрерывно дифференцируема по (z,p), тогда

1. (t,s,z,p) непрерывно дифференцируема l раз по (z,p)

2. все производные функции по (z,p) до порядка (l-1), включительно непрерывно дифференцируемы по (t,s,z,p)

Линейные ДУ. Общие свойства.

y=A(t)y+f(t) (1а) линейность по y

y|_t=s=z (1б)⁽¹⁾

Замечание. Из теоремы Пикара следует ! решения задачи (1), если функции A, f непрерывны.

Теорема: 1 (Теорема и!)

Обобщенное решение (1) и единственно наинтервале, на котором функции A(t), f(t) суммируемы.

Замечание: Для векторной формы явного решение нет и быть не может (кроме редких случаев).

Теорема: 2 (Оценка решения)

|y(t)|<(|A|- операторная норма матрицы)

Теорема: 3 (предельный переход в задаче Коши)

Рассмотрим задачу Коши (1). Предположим, что z_nz₀, A_nA₀, f_nf₀(норма разности0)

Пусть y₀– решение задачи Коши для A₀, z₀, f₀, тогда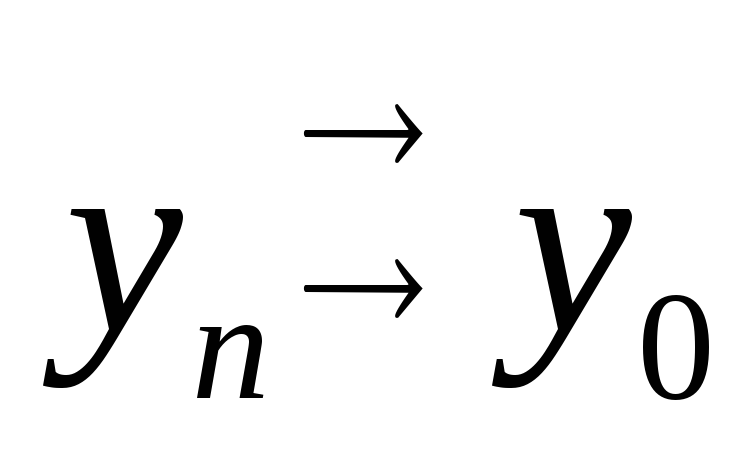

Линейные однородные ДУ.

ДУ вида y=A(t)y (1)

Следствие: из теоремы единственности.

Если решение y(t) уравнения (1)=0, хотя бы в одной точке, то y(t)=0 (по теореме единственности y(t)=0 – всегда решение (1))

Теорема: 1

1. Множество решений (1) образует линейное подпространство размерности n (если yСⁿ)

2. Для набора решений {y₁(t), y₁(t),…} и дляточек t₁,t₂: линейная независимость столбцов

{ Y_k(t₁)}ЛНЗ { Y_k(t₂)}

Замечание: След матрияы A (TrA или SpA) TrA=a₁₁+ a₂₂+…+ a_nn=_ka_kk

Теорема: 2 (формула Лиувиля)

det(Y(t))=det(Y(S)) (2)

Опр: Фундаментальной системой решений ДУ (1) называется любой базис в пространстве решений.

Теорема: 3 (свойства разрешающей матрицы)

Пусть U(t,s) – разрешающая матрица, тогда

1. Решение задачи Коши с начальными значениями задается формулойy(t)=U(t,s)z

2. U(t,s)=Y(t)Y^-1(s) (фундаментальная матрица Y)

3. Групповое свойство:

U(t₁,t₂)U(t₂,t₃)=U(t₁,t₃)

U(t₃,t₁)=U^-1(t₁,t₃)

Линейные неоднородные уравнения

y'=A(t)y (0)

y'=A(t)y+f(t) (1)

Теорема: 1 (принцип суперпозиции)

1. Пусть y_о.о.(t,c₁,c₂,…,c_n) – общее решение однородного уравнения (0)

у_ч.н.(t) – частное решение неоднородного уравнения (1), тогда общее решение (1) имеет вид:

y(t,c₁,c₂,…,c_n)=y_o.o.(t,c₁,c₂,…,c_n)+y_ч.н.(t)

2. Пусть y₁(t) – решение (1) для f=f₁

y₂(t) – решение (1) для f=f₂, тогда (y₁+y₂) – решение (1) для f=f₁+f₂

Теорема: 2 – метод вариаций произвольной постоянной.

Функция y(t) – решение (1) <=> y(t)=Y₀(t)u(t), где Y₀(t) -фундаментальная матрица для (0)

u(t) – обобщенное решение уравнения Y₀(t)u'=f

Линейное уравнение с постоянными коэффициентами

y=Ay (0)

y'=Ay+f(t) (1) A – постоянная матрица

Частный случай y – скаляр, y'=ay <=> y(t)=Ce^at

Теорема: 1) Ряд для e^Atсходится равномерно наограниченном интервале от t.

2) |e^At|<e^|A||t|, где ||- операторная норма матрицы

3. Матрица e^A(t-s) является разрешающей для уравнения (0)

Теорема: 2 :Жорданова клетка J. e^Jt=e^t=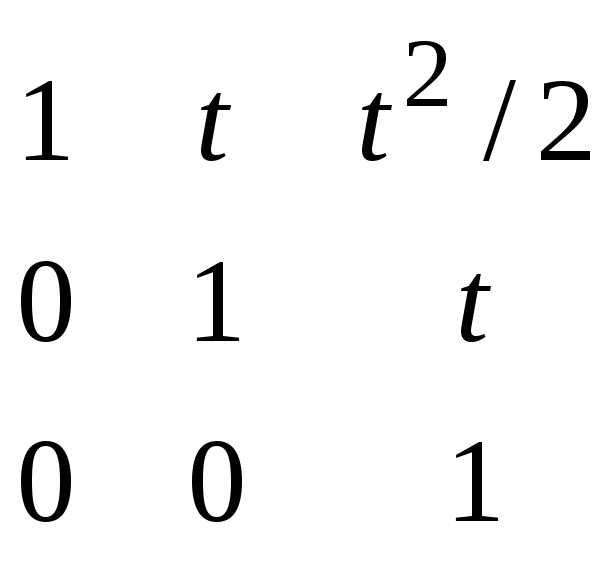

Экспоненциальная дихотония

Пусть матрица А не имеет чисто мнимых собственных чисел ( в том числе = 0 ) тогда пространство решений распадается на сумму двух подпространств в одном из которых все решения экспоненциально возрастают при t+и экспоненциально убывают при t

А в другом подпространстве наоборот.

Линейные уравнения высших порядков

Утв: Пусть u₁, u₂, …,u_n решение (0), тогда

1. {U_k(t)} – линейно независимы => W_u1,u2(t)0t, (т.к. => {y_k(t)} – линейно независимыt)

2. {U_k(t)} – линейно зависимы => W_u1,u2(t)=0

Формула Лиувилля

W_u1,u2,…,un(t)=W _u1,u2,…,un(s)(<= det Y(t)=det Y(s)

В частности P_n-1(t)=0, то W_u1,u2,…,un=const

Теорема:

1. P() – характеристический многочлен уравнения u⁽ⁿ⁾+p_n-1u^(n-1)+…+p₀u=0 (0), P()=det(I-A)

2. Общее решение (0) имеет вид:

u(t,c)=_me^mt

где {C_mi} – произвольная постоянная

km – алгебраическая кратность корня _mдля характеристического многочлена.

Замечание: Любые собственные числа матрицы А представлено жордановой клеткой максмально большого размера, т.е. одной, иначе в y(t)=_me^mtне могли появиться слагаемые с максимально возможной степенью, not e^mtt^km-1

Линейные уравнения с периодическими коэффициентами (векторные L-го порядка)

Задача вида y'=A(t)y (1)

Теорема: Своства матрицы Мондроми

1. V(t+p,s+p)=V(t,s)

2. Матрица М коммутирует с разрешающей

3. Пусть Y(t) - фундаментальная матрица, тогда матрица N=Y^-1(t)MY(t)

4. Если Y – фундаментальная матрица, то произведение от t не зависит det M=

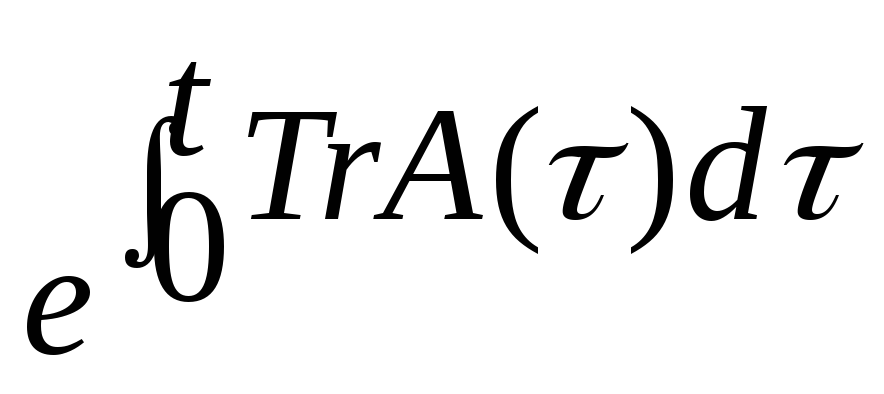
Теорема: 2 Пусть J – жорданова клетка, отвечающая собственным числам => матрица

L=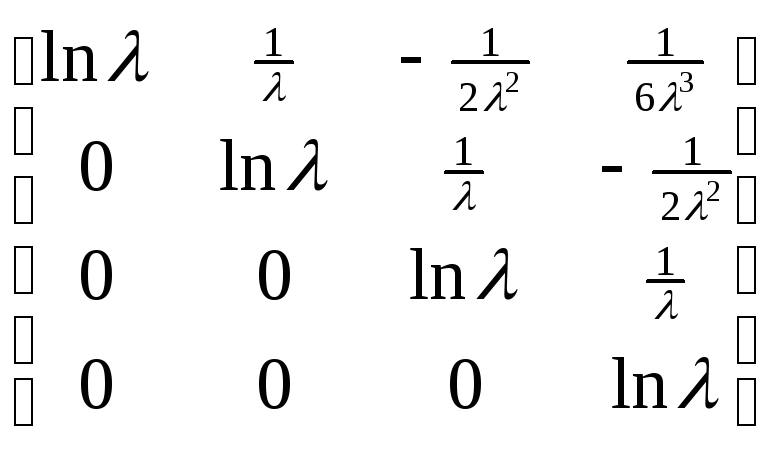удовлетворяет соотношению e^L=J

Теорема: 3 Представление Флоке

Пусть Y(t) = любая фундаментальная матрица, тогда

1. Y(t) – можно представить в виде Y(t)=F(t)e^KT, где K – постоянная матрица, а F(t) – p-периодичесткая матрица, т.е. F(t+p)=F(t)

2. K=¹/_pY^-1(0)lnMY(0), через матрицу Мандроми.

Замечание:

Для частного случая, если Y(t)=U(t,0), то Y(0)=U(0,0)=I=>K=¹/_plnM=>e^Kt=e^t/plnM=M => представление Флоке имеет вид U(t,0)=F(t)M^t/p