
- •Предисловие
- •Правовые вопросы
- •1. Иерархия математических моделей эфира как сплошной среды
- •1.1. Микроуровневая и макроуровневая модели эфира
- •1.2. Сравнение уравнений эфира с классическими уравнениями механики сплошной среды
- •1.3. Инвариантность уравнений неразрывности и движения эфира относительно преобразования Галилея
- •1.4. Плотность энергии, плотность мощности эфира. Давление эфира. Уравнение состояния эфира
- •2. Вывод уравнений Максвелла из уравнений эфира
- •2.2. Вычисление электрического и магнитного полей
- •2.3. Векторный потенциал. Физическая интерпретация
- •2.5.2. Преобразование производных и операторов при замене переменных Галилея. Инвариантность уравнений неразрывности и движения эфира в эйлеровых переменных
- •2.5.3. Причина потери галилеевой инвариантности в обобщённых уравнениях Максвелла – неинвариантное преобразование исходных уравнений эфира. Инвариантность обобщённых уравнений Максвелла при досветовой скорости движения системы координат
- •2.5.4. Галилеева неинвариантность классических уравнений Максвелла в отсутствие среды и их инвариантность в эфирной трактовке при досветовой скорости движения системы координат
- •2.6. Общие замечания
- •3. Заряд, его электрическое поле. Теорема Гаусса. Закон Кулона. Электрический потенциал. Связь потенциального электрического поля с градиентом давления эфира. Сохранение заряда
- •4. Волновые процессы в эфире
- •5. Энергия электромагнитного поля
- •5.1. Общие формулы для плотностей энергии и мощности электромагнитного поля
- •5.2. Плотность энергии электромагнитной волны
- •5.3. Интерпретация энергии кванта света, постоянной Планка, волны де Бройля
- •6. Разрывы в эфире. Эффекты квантования
- •6.1. Самопроизвольное формирование разрывов
- •6.2. Условия на поверхности разрыва
- •6.3. Пример квантования
- •6.4. Эфирное представление условий разрыва магнитного и электрического полей
- •7. Вывод закона Био – Савара из уравнений эфира
- •8. Индуктивность геометрического объекта, создающего магнитное поле
- •9. Основной закон электромагнитной индукции. Электродвижущая сила. Правило Ленца
- •10. Вихревой импульс эфира. Закон сохранения вихревого импульса. Сохранения момента магнитного поля
- •12. Электрический ток в проводниках
- •12.1. Токи вне и внутри проводников. Законы Ампера
- •12.2. Закон Ома. Электрическая проводимость
- •12.3. Закон Джоуля и Ленца
- •12.4. Влияние распределения скорости эфира внутри провода на создаваемое в нём магнитное поле и плотность электрического тока
- •12.5. Сверхпроводимость
- •13. Силовое воздействие эфира на объект, вызванное наличием градиента давления
- •14. Эфирный аналог теоремы Бернулли
- •15. Классификация установившихся потоков эфира
- •15.1. Электрический поток эфира
- •15.2. Гравитационный поток эфира
- •15.3. Магнитный поток эфира
- •16. Силовое воздействие потока эфира на объект
- •16.1. Воздействие на заряженный объект. Сила Лоренца
- •16.2. Сила эфирного гравитационного притяжения
- •17. Взаимодействие объектов
- •17.1. Закон Кулона для двух заряженных объектов
- •17.2. Закон гравитационного тяготения
- •18. Эфирная трактовка в электротехнике и электрохимии
- •18.1. Создание электрического тока в проводе. Падение напряжения на участке цепи
- •18.2. Мощность электрической цепи
- •18.3. Электрическое сопротивление в электрохимической ячейке и газовом разряде
- •18.4. Электрическое сопротивление в проводе
- •18.5. Электроёмкость, конденсаторы
- •18.6. Уравнение тока в контуре постоянной формы
- •18.9. Полная электромагнитная мощность цепи с током. Вектор Умова – Пойнтинга
- •18.10. Взрыв проволочек электрическим током в вакууме. Взрывная электронная эмиссия
- •18.11. Э.д.с. Жуковского. Униполярный генератор
- •18.12. Эффект Холла. Постоянная Холла
- •18.13. Электростатические эффекты
- •18.14. Электростатические устройства
- •18.15. Удержание плазмы в тороидальных ловушках. Обобщение математических моделей плазмы
- •19. Интерпретация магнитных явлений
- •19.1. Поток эфира, создаваемый доменом
- •19.2. Магнит и ферромагнитный материал
- •19.3. Проводящий немагнитный материал и магнит
- •19.4. Проводник с током и магнит
- •19.5. Взаимодействие магнитов друг с другом
- •19.6. О попытках создания двигателя или генератора энергии на основе перемещения системы постоянных магнитов
- •20. Оценка плотности невозмущённого эфира
- •20.1. Единицы измерения плотности эфира
- •20.2. Оценки на основе экспериментов с лазерами
- •20.3. Оценки с использованием эфирной модели фотона и характеристик электромагнитного поля в нём
- •20.4. Оценка из эфирной модели фотона и его импульса
- •20.5. Оценки с применением эфирных моделей электрона и протона
- •20.6. Оценка на основе данных о кулоновском барьере
- •20.7. Основные выводы. Значение плотности эфира
- •20.8. Ошибочность принятия диэлектрической проницаемости вакуума в качестве невозмущённой плотности эфира
- •21. Структура носителей эфира – ньютониев. Кинетические эффекты в эфире и веществе
- •21.1. Давление невозмущённого эфира
- •21.2. Масса и размер носителей эфира – ньютониев. Среднее расстояние между ними
- •21.3. Распределение ньютониев при хаотическом тепловом и направленном движении
- •21.4. Краткий обзор моделей неравновесных, необратимых процессов и коэффициентов переноса в физике. Применение к описанию кинетики ньютониев
- •21.5. Теплопередача в эфире. Теплоёмкость эфира
- •21.6. Теплопередача в твёрдом веществе
- •21.7. Вязкость эфира
- •21.8. Самодиффузия в эфире
- •21.9. Электрическая проводимость эфира и вещества при отсутствии свободных зарядов
- •21.10. Оценка параметров эфирной модели электропроводности по опытным данным
- •21.11. Закон Видемана и Франца в металле и эфире
- •21.12. Давление эфира внутри твёрдых материалов и жидкостей
- •21.13. Слипание пластин с гладкой поверхностью, эффект Казимира. Фазовый переход состояний объектов. Радиоактивный распад
- •21.14. Явления в контактах
- •21.15. Электроотрицательность химических элементов
- •22. Оценка радиусов пограничных слоёв, обуславливающих возникновение силы Лоренца и силы гравитации
- •22.1. Заряженные объекты
- •23. Сводка экспериментальных фактов, подтверждающих наличие эфира
- •23.1. Основные общие законы электродинамики и гравитации
- •23.2. Электрический ток в проводе
- •23.2.1. Внутренняя противоречивость модели свободных электронов в твёрдом проводнике
- •23.2.2. Проблемы интерпретации опытов в электронной теории проводимости
- •23.2.3. Расчёт течения эфира внутри провода
- •23.3. Эксперименты с униполярным генератором. Эффект Аспдена
- •23.5. Теплопроводность металлов
- •23.5.1. Теплопроводность в поле силы тяготения
- •23.5.2. Теплопроводность во вращающемся диске
- •23.5.3. Теплопроводность при наличии вибрации
- •23.6. Вращение тел при отсутствии внешнего магнитного поля
- •23.6.1. Опыт Толмена и Стюарта с вращающейся катушкой
- •23.6.2. Инерционный опыт Лепёшкина с вращающейся спиралью
- •23.6.3. Создание магнитного поля вращающимся сверхпроводником, ферромагнетиком и другими объектами. Момент Лондона. Эффект Барнетта. Гравитомагнитный момент Лондона
- •23.6.4. Создание в эфире фантома вращением магнитного диска
- •23.6.5. Электромагнитное поле, создаваемое камертоном
- •23.6.6. Магнитное поле вращающегося немагнитного диска. Проект экспериментов
- •23.6.7. Опыт с вращающимся диском и флюгером
- •23.6.8. Ошибочные трактовки движения объектов в некоторых опытах как результата механического взаимодействия с эфиром
- •23.7. О разрушении материала вращением
- •23.8. Разрушение материала лазером
- •23.9. Эксперименты в техническом вакууме
- •23.9.1. Темновой ток
- •23.9.2. Темновой ток в присутствии магнита
- •23.9.3. Мельничка
- •23.9.4. Коловрат
- •23.9.5. Несимметричные конденсаторы. Эффект Бифельда – Брауна. Лифтер. Модифицированный коловрат
- •23.9.6. Автоэлектронная эмиссия и фотоэмиссия электронов из проводника
- •23.9.7. Пробойный ток
- •23.10. Противодействие гравитации. Экранировка гравитационного потока эфира
- •23.10.1. Вращение частично сверхпроводящего керамического диска в магнитном поле. Противодействие гравитации в эксперименте Подклетнова
- •23.10.2. Уменьшение веса электрона в вакуумной трубке, окружённой сверхпроводником, за счёт экранировки гравитационного потока эфира
- •23.10.3. Экранировка гравитационного потока эфира атомарным порошком
- •23.10.4. Проект стенда для опытов с гравитацией
- •23.11. Черенковское излучение в эфире
- •24. Эфирная модель шаровой молнии
- •24.1. Аномальные свойства ШМ
- •24.2. Попытки объяснения ШМ без учёта эфира
- •24.3. Простейшая эфирная модель ШМ. Трактовка аномальных свойств
- •24.4. Интерпретация экспериментов Теслы с ШМ. Резонансный механизм аномальных явлений в электротехнических устройствах
- •25. Эфирная модель строения Земли
- •Заключение
- •Приложение 1. Вывод уравнения Ампера
- •Приложение 2. О поисках эфирного ветра
- •Приложение 3. О движущихся источниках света
- •Приложение 4. Траектории лагранжевых частиц для уравнения движения с нулевой правой частью
- •Приложение 5. Новые системы единиц измерения, связанные с эфиром
- •Приложение 6. Концентрации электронов и ионов в воздухе при низком давлении
- •Приложение 7. Ионный ветер в коронном разряде
- •Литература
- •Литература, добавленная во 2-м издании
- •Представления некоторых великих учёных об устройстве материи
- •Цитаты из высказываний о первом издании книги

vk.com/club152685050 | ГУАП
Учитывая |
|
|
|
|
|
|
(216) |
|||||||
= /(2 ), имеем |
|
|
||||||||||||
|
|
|
|
|
|
|
0 = |
|
2 |
|
. |
|
|
|
Формула |
|
для энергии |
|
|
|
|||||||||
тах со светом. |
|
|
|
[Гц] |
фотона установлена в эксперимен- |
|||||||||
|
|
|
= 6 ∙ 10 |
|
|
|
|
|
|
|||||
ния. Если для |
Поэтому рассмотрим характерную частоту види- |
|||||||||||||
|
14 |
|
|
. |
|
|
|
|
||||||
мого света |
|
|
|
|
|
|
|
= 10 |
|
|||||
|
|
, близкую (по порядку величины) к |
|
|||||||||||
Величина |
|
|
определяется свойствами источника излуче- |
|||||||||||
(220), |
0 |
|
|
источника света положить |
|
, то получим |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(217) |
||
оценку |
|
|
|
|
|
|
|
|
|
|
|
|
значениям (215) и |
|
найденным без использования ,
0
20.4. Оценка из эфирной модели фотона и его импульса
Приведённые выше оценки плотности невозмущённого эфира проводились на основе колебательных характеристик электромагнитных явлений. Здесь воспользуемся механическими представлениями и известным из эксперимента свойством света оказывать давление на тела.
Оценимсначалаплотностьневозмущённогоэфиравмехани-
ческих единицах измерения |
|
, исходя из импульса одного фо- |
|||
тона,имеющегообъём |
|
(216).Вэфирноймоделифотона(214) |
|||
|
|
|
|
,0 |
|
|
доминирует скорость в направлении его распро- |
||||
существенно |
|
|
|
|
|
тромагнитной волны, приближённо равен ,0 . Приравнивая эфирное представление импульса фотона экс-
странения. Поэтому импульс фотона, состоящего из одной элек-
периментально установленному / , с учётом возможности
291
Скачать http://eth21.ru | правкой от 13.04.2019

vk.com/club152685050 | ГУАП
,0 |
|
= / . |
|
|
|
электромагнитных |
|
волн |
имеем |
||||||||||||||||||
наложения |
|
в фотоне |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
Отсюда, используя (216), |
|
|
|
|
|
|
|
|
|||||||||||
находим |
|
|
|
,0 = |
2 |
= |
3 2 |
. |
|
= 6 ∙ 10 |
[Гц] |
|
|
||||||||||||||
|
|
Для характерной частоты видимого света |
|
|
|
14 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
,0 |
|
|
|
|
|
|
к |
|
= 10 |
|
|
|
|
|
|
|
|||||
Если, как и в |
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
(218) |
|||||||||||
где значение |
|
определяется свойствами источника фотонов. |
|||||||||||||||||||||||||
|
|
|
|
|
|
предыдущем пункте, взять |
|
|
|
|
, то |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
,0 |
,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
натурных |
|
|
|
теперь |
на |
|
основе |
эфирной |
интерпретации |
||||||||||||||||||
|
|
Оценим |
|
|
|
|
|
||||||||||||||||||||
|
|
|
экспериментов по определению давления света. Рас- |
||||||||||||||||||||||||
смотрим поток фотонов, падающих на тело массой |
. Обозна- |
||||||||||||||||||||||||||
чим суммарную энергию потока фотонов буквой |
|
. Пусть |
энер- |
||||||||||||||||||||||||
действия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
гия |
|
полностью поглощается данным телом. |
|
|
|
|
|
|
|
||||||||||||||||||
|
Если |
|
значительно превышает энергию тела до начала воз- |
||||||||||||||||||||||||
|
|
|
фотонов, то можно приблизительно записать |
|
|
|
|
. |
|||||||||||||||||||
Отметим, что приравнивать |
только кинетической |
энергии тела |
|||||||||||||||||||||||||
|
≈ |
|
|
||||||||||||||||||||||||
нельзя, так как энергия фотонов |
идёт и на увеличение внутрен- |
||||||||||||||||||||||||||
ней энергии тела. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
С учётом обсуждённой выше возможности наложения элек- |
|||||||||||||||||||||||||
тромагнитных волн в фотоне, для числа |
|
падающих на тело |
|||||||||||||||||||||||||
единичных электромагнитных волн имеем |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= / .
292
Скачать http://eth21.ru | правкой от 13.04.2019

vk.com/club152685050 | ГУАП
,0 |
|
|
|
Так как одна электромагнитная волна несёт импульс |
|
|
|
, то из свойства суперпозиции скорости эфира в безди- |
вергентном поле скоростей [50, 52] и закона сохранения импульса имеем
,0 = или ,0 |
|
= |
|
. |
||||
/ |
|
|||||||
Тогда |
,0 = |
2 |
. |
|
|
|||
|
|
|
|
|
||||
делаПолучилась. |
тажеформуладля ,0 |
,чтоивначалеэтогораз- |
||||||
20.5.Оценки с применением эфирных моделей электрона и протона
В работе [49] на основе приближённого решения уравнений эфира (1), (2) получены аналитические формулы для описания установившихся состояний электрона, протона и нейтрона. Свободные параметры аналитических решений откалиброваны в соответствии с известными экспериментальными сведениями о заряде,массеимагнитноммоментеэлектрона,протонаинейтрона. Показано, что различие теоретических рассчитанных и экспериментальнополученныхзначенийдлязаряда,массыимагнитного
момента электрона и протона составляет лишь |
. Такая же |
|||||
погрешность имеет место и для массы и |
магнитного момента |
|||||
|
~0.1 % |
|||||
нейтрона. |
|
найдём |
0 .0 |
|
|
|
метра , а затем по |
|
|
|
|
||
Эфирные представления характеристик элементарных ча- |
||||||
0 |
0 |
|
2930 |
. Получим оценку для пара- |
||
стиц содержит произведение |
|
|||||
Скачать http://eth21.ru | правкой от 13.04.2019
vk.com/club152685050 | ГУАП
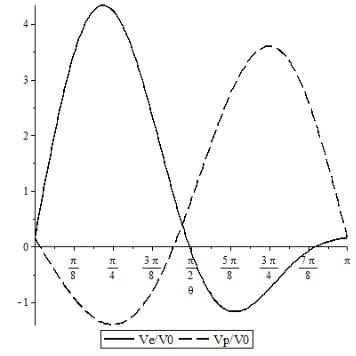
Рассмотрим область( , , ,значений) переменных, в которой радиальная скорость =[49], точки эфира направлена к цен-
тру элементарной частицы
|
|
( , , , ) = |
|
|
cos − /2 < 0, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
: |
|
|
|
−, |
|
,<а /2 |
|
|||||
электронов |
|
|
|
|
|
|
/2 < , − /2 |
|
||||||||
Согласно формуле (9) из [49], заряд и константа |
|
имеют |
||||||||||||||
тонов |
|
|
: = |
|
,1 |
≤ |
≤, ,2 |
,1 ≈ 0, ,2 ≈ /2 |
|
(рис. 9). |
||||||
одинаковый |
знак. Тогда |
при |
|
≈ |
/32 ,2 ≈ 7 /16 |
0 |
|
для |
||||||||
|
|
= |
|
,1 |
≤ ≤ ,2 ,1 |
для про- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 9. Функции ( )/ 0.
294
Скачать http://eth21.ru | правкой от 13.04.2019

vk.com/club152685050 | ГУАП
Константы , , в формуле для ( ), = , , определены с помощью вычисления интегралов. Погрешности приближений
различных величин при получении оценок должны быть согла-
сованы. Поэтому упростим выражение для радиальной скорости, |
|||||||||||||
заменив, |
|
на среднее по части поверхности, где ( , , , ) < |
|||||||||||
0 |
|
,1 |
− /2 |
|
|
|
|
|
|
|
| 0| |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
,1 |
|
/2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
( ) ≡ |
|
∫ ,1 |
∫− /2 2 sin |
|
= − , |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение движения по координате со средней скоростью |
|||||||||||||
имеет решение |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
∆ = |
||||
|
|
|
|
|
|
|
|
(изменение |
|
|
|
||
Знак радиальной скорости не меняется (то есть точка |
( ) |
||||||||||||
( + )/ − ( − )/ |
= 2 / |
|
|
|
|
|
|||||||
движется в одном направлении) |
на промежутке времени |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
направления |
||
движенияможетвозникнуть,например,из-засменызнакадивер- |
||||||||||||||
|
2 |
( ) |
|
2 |
|
2, где |
|
|
|
|
(0) |
|
|
траекто- |
генции в уравнении движения [50]). Пусть за время |
|
|||||||||||||
бы(0) − |
(0) |
|
0 < < 1 |
|
= 1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
положение |
|
рия |
|
смещается из начального положения 2 |
|
в∆ |
|
|||||||||
|
до центра частицы). Тогда |
(при |
|
смещение доходило |
||||||||||
|
0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
295 |
|
|
|
|
|
|
|
Скачать http://eth21.ru | правкой от 13.04.2019

vk.com/club152685050 | ГУАП
Отсюда |
|
|
|
|
|
|
|
| 0| = 2 |
(0) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(0) [0, ] |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или в среднем (с учётом якобиана) по всем стартовым точкам |
||||||||||||||||||||||||||||||||||
| 0 |
| = |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= |
|
|
|
|
|
2 |
= |
|
|
|
2. |
||||||
|
|
2 |
|
) |
|
|
|
( |
|
) |
4 |
20 |
|
|
|
20 |
||||||||||||||||||
|
|
|
0 |
|
|
( |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= , , полу- |
||||
чаем оценку снизу для параметра 0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Заменив правую часть на минимальную по |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
≥ |
20 |
|
2 ≈ 4.8 ∙ 10−5 2 [см2/c]. |
|
|
|
|
|
|||||||||||||||||||
|
Оценку сверху для |
|
|
найдём из ограничения на величину |
||||||||||||||||||||||||||||||
скорости свободного |
распространения возмущений в эфире |
|||||||||||||||||||||||||||||||||
|
| 0| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
– азимутальная скорость движения эфира в частице . |
||||||||||||||||||||||||||||||||
|
Заменим скорости на средние по поверхности: |
|
и |
|
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
≡ |
|
,1 |
− /2 |
|
|
|
|
|
|
|
|
|
≈ 0.74 |
. |
|
|
|
|
||||||||||||
|
|
|
|
∫ ,1 |
∫− /2 |
2 sin |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
,1 |
|
/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
296 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Скачать http://eth21.ru | правкой от 13.04.2019

vk.com/club152685050 | ГУАП
Тогда |
|
|
|
+ 0.74 2 |
2. |
|
||
Отсюда |
0 |
|
||||||
|
|
0 |
|
|
|
|
|
|
|
|
| | |
1 − 0.74 . |
|
||||
|
|
|
|
|
|
|
|
|
Оценка должна выполняться для всех из области примени- |
||||||||
0.15 |
≤ |
|
|
|
|
, находим |
|
скорости: |
мости |
аналитической |
формулы для радиальной |
||||||
|
[0.15 , 0.96 ] |
|
|
|||||
|
|
|
|
|
|
|
||
|
|
. Тогда, учитывая монотонное возрастание правой |
||||||
части на
Оценка должна иметь место как для электронов, так и для протонов
0 |
=, |
|
|
|
|
|
|
||
Итак, |
|
|
0
Здесь величина является параметром, который характеризует величину среднего смещения эфира в радиальном направлении.
297
Скачать http://eth21.ru | правкой от 13.04.2019
vk.com/club152685050 | ГУАП
Для определения конкретного значения |
|
необходимы дополни- |
||||||||||||||
для заряда (9) из [49] |
|
|
|
0 |
|
|
|
|||||||||
тельные исследования. |
|
|
|
|
вычислим по формуле |
|||||||||||
|
|
Плотность невозмущённого эфира |
|
|
||||||||||||
|
|
|
|
|
|
|
0 |
= 1 + 4 / 0. |
|
|
|
|
(219) |
|||
|
|
С учётом полученной выше оценки |
| 0| имеем |
|||||||||||||
|
3.6 ∙ 10−16 0 1.1 ∙ 10−15 |
2 [c г1/2/см3/2], |
0 < < 1. |
|||||||||||||
г |
|
/см |
|
|
] |
даёт |
|
|
, |
| 0|.≈ 1.8 ∙ 10 |
0, |
≈ 3 ∙10−13 [c ∙ |
||||
/2 |
3/2 |
|
2 |
≈ 0.004 |
−7 |
| 0|/ ≈ 4.6 ∙ |
||||||||||
103 |
[см/c] |
|
|
| 0|/ ≈ 8.5 ∙106[см/c] |
|
|
эфира |
|
|
|||||||
|
|
Отметим, что величина плотности |
|
|
||||||||||||
|
|
|
|
, |
|
|
|
|
|
Поэтому с большим запа- |
||||||
сом выполняется предположение о малой по сравнению со скоростью света радиальной скорости, использованное при получении аналитических выражений для движения эфира в элементарной частице [49].
Оценка величины радиальной скорости в электроне и протоне позволяет объяснить меньшую сопротивляемость электрона к проникновению в него объектов. Средняя радиальная скорость эфира в электроне значительно меньше средней радиальной скорости эфира в протоне. Поэтому эфир в электроне сообщает значительно меньший радиальный импульс проникающемувнегообъекту~200,оказываяменьшеесопротивление.Вмюоне (уменьшенный~200 в раз электрон) радиальная скорость эфира в ~200больше, чем в электроне, и в этом смысле мюон оказывает в раз большее сопротивление проникновению, чем электрон. Данное обстоятельство соответствует экспериментальным наблюдениям [53], показывающим малое время жизни мезоатома водорода.
298
Скачать http://eth21.ru | правкой от 13.04.2019
