
- •Передмова
- •Точки і кола, дуги і кути на сфері.
- •Сферичний кут, його вимірювання та властивості. Суміжні та вертикальні кути.
- •Елементарні задачі на побудову на сфері.
- •Іv. Питання для самоконтролю:
- •V. Література
- •І. План лекції
- •Іі. Основні типи задач.
- •Ііі. Короткі теоретичні відомості.
- •1. Поняття сферичного трикутника, його елементи. Вимірювання сторін і кутів сферичного трикутника
- •Суміжні та симетричні трикутники, їх властивості
- •6. Побудова трикутника на сфері:
- •7. Довести нерівності:
- •Іv. Питання для самоконтролю.
- •Теорема синусів.
- •Співвідношення між елементами прямокутного сферичного трикутника
- •Іv. Питання для самоконтролю.
- •Література
- •І. План лекції.
- •Іі. Основні типи задач.
- •Ііі. Короткі теоретичні відомості.
- •1. Послідовність операцій при розв’язанні сферичних трикутників:
- •2. Розв’язання сферичних трикутників
- •Шість основних типів задач розв'язання прямокутних сферичних трикутників
- •4. Приклади розв’язання задач
- •Іv. Питання для самоконтролю.
- •Література
- •І. План лекції.
- •Ііі. Короткі теоретичні відомості
- •1. Визначення місця знаходження точки на земній кулі.
- •Обчислення градусної міри сторін і кута одержаного сферичного трикутника та відстані між двома пунктами
- •3. Розв’язування задач.
- •IV. Питання для самоконтролю
- •1. Небесна сфера та її елементи
- •2. А) визначення положення світила на небесній сфері у системі горизонту.
- •2 Б). Визначення положення небесних світил у екваторіальній системі координат
- •Задачі з астрономії та їх розв’язування
- •IV. Питання для самоконтролю.
- •V. Література
- •2. Зразки завдань для закріплення лекційного матеріалу:
- •4. Зразки завдань для підготовки до виконання ргр
Шість основних типів задач розв'язання прямокутних сферичних трикутників
Дано |
Знайти |
Формули для обчислення шуканих елементів |
|
Гіпотенузу
кути
|
(2):
(6): (6):
|
2.
Гіпотенуза
і катет
|
Катет
кути
|
(8): З
(7):
З
(4):
Тоді
|
3. Гіпотенуза
і
прилеглий кут
|
Катети
кут |
З
(10):
З
(7):
З
(3):
|
4. Катет та протилежний кут
|
Катет гіпотенузу кут |
(6): звідки
З
(7):
З (3):
|
5. Катет та прилеглий кут
|
Катет гіпотенузу кут |
(6): звідки
З
(10):
З
(10):
З
(9)
|
6. Дано два кути та прилеглі до гіпотенузи
|
Катети
гіпотенузу
|
З
(9):
З
(9):
З
(9):
|
4. Приклади розв’язання задач
а) Розв’язати сферичний трикутник, у якого:
а = 790331 , b = 650281, с = 370531
Розв’язання
Перевіримо, чи існує трикутник з такими сторонами.
00 < а = 790331 < 1800, 00 < b = 650281 < 1800, 00 < c = 370531 < 1800,
a+b = 790331 + 650281 = 1450011 > c = 370531,
a+c = 790331 + 370531 = 1170261 > b = 650281,
b+c = 650281 + 370531 = 1030211 > a = 790331.
Трикутник з такими сторонами може існувати.
Дано |
Знайти |
Формули для обчислення шуканих елементів |
1. Три сторони
|
Кути
|
(2):
|
Обчислення кута А.
cosa
= cosb
cosc
+ sinb
sinc
cosA,
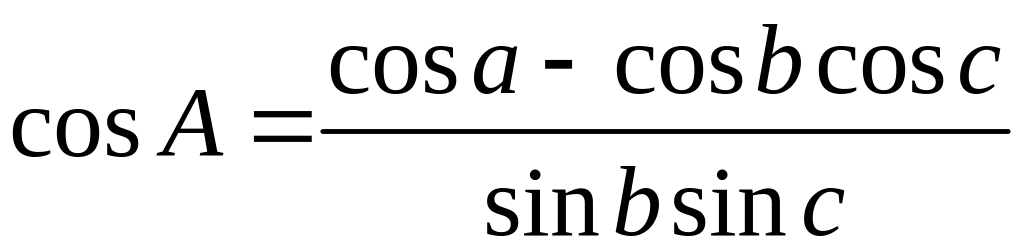 ,
,
cosa = cos790331 = 0,1814,
cosb = cos650281 = 0,4152,
cosc = cos370531 = 0,7893,
cosb cosc =0,4152*0,7893= 0,3277,
sinb = sin 650281 = 0,9097,
sinc = sin 370531 = 0,6141,
sinb sinc = 0,9097*0,6141=0,5586,
cosa – cosb cosc= 0,1814 - 0,3277= - 0,1463,
=
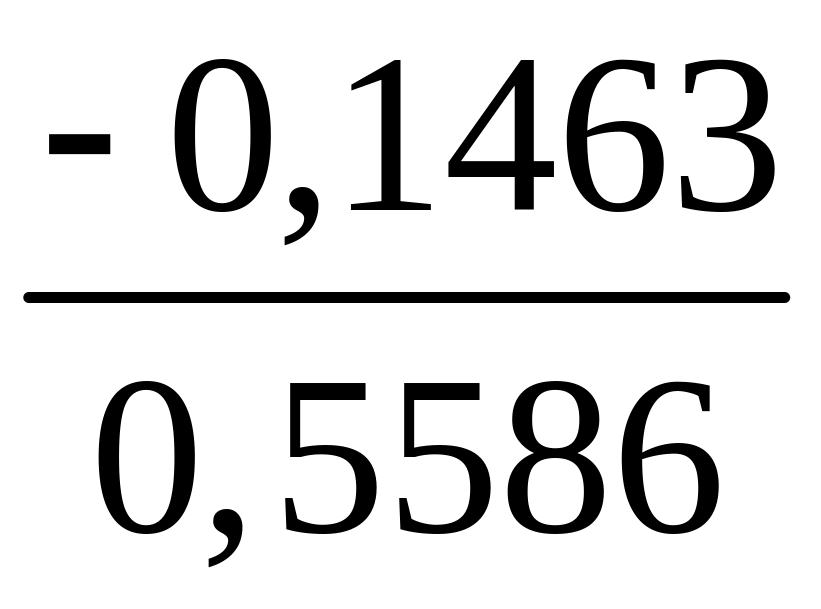 =-0,2619,
=-0,2619,
A=arccos(-0,2619)=1800-arccos 0,2619=1050101.
Обчислення кута В.
|
Контроль обчислень
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
|
Обчислення кута С
0,4152, 0,1814, 0,7893,
0,9834,
|
Контроль обчислень
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними. (Перевірку виконати самостійно) |
Відповідь:
![]() ,
,
![]() ,
,
![]()
б)
Розв’язати
сферичний трикутник, у якого
![]() ,
,
![]() ,
,
![]() .
.
Розв’язання.
Перевіримо, чи існує сферичний трикутник з такими кутами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Трикутник з такими кутами може існувати.
Дано |
Знайти |
Формули для обчислення шуканих елементів |
Три кути сферичного трикутника
|
Сторони трикутника
|
(3):
|
Обчислення сторони :
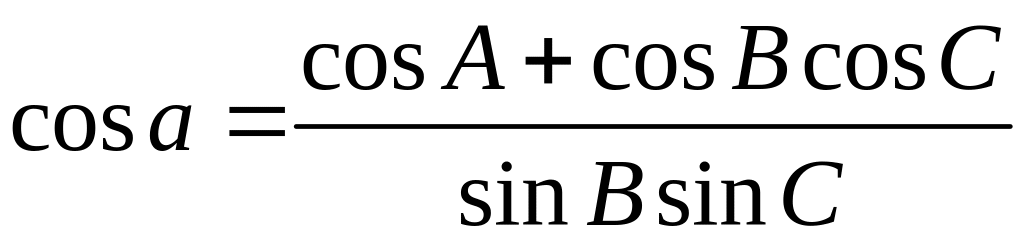 ,
,
![]() -0,3051,
-0,3051,
![]() 0,3469,
0,3469,
![]() -0,6580,
-0,6580,
![]() -0,2283,
-0,2283,
![]() -0,3051-0,2283=-0,5334,
-0,3051-0,2283=-0,5334,
![]() 0,9379,
0,9379,
![]() 0,7530,
0,7530,
![]() 0,7062,
0,7062,
![]() -0,7553,
-0,7553,
![]()
Обчислення сторони .
-0,3051, 0,3469, -0,6580,
0,7530,
|
Контроль обчислень
0,6554*0,9379=0,6147,
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
|
Обчислення сторони .
-0,3051, 0,3469, -0,6580,
0,9523, 0,9379,
|
Контроль обчислень
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними. (Перевірку виконати самостійно) |
Відповідь:
![]() ,
,
![]() ,
,
![]() .
.
в) Розв’язати сферичний трикутник у якого:
![]() ,
,
![]() ,
.
,
.
Перевіримо, чи існує сферичний трикутник з такими елементами.
![]() ,
,
![]() ,
,
![]() .
.
Отже, з такими даними сферичний трикутник може існувати.
Дано |
Знайти |
Формули для обчислення шуканих елементів |
Гіпотенуза с і катет b
|
Катет а та кути А і В |
(8)
(1)
(4)
|
Обчислення катета а.
;
![]() ;
;
![]() ;
;
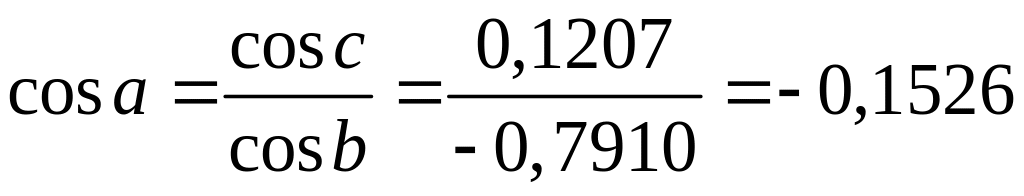 ,
,
![]() ,
,
Обчислення кута В:
;
![]() ,
,
![]() ,
,
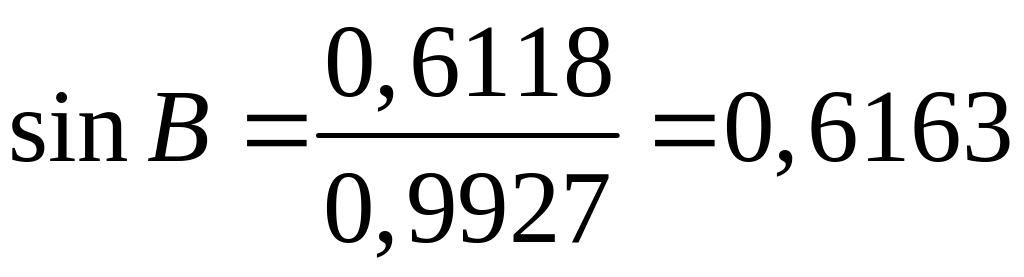 ,
,
![]() або
або
![]() ,
,
Обчислення кута A: ;
|
Контроль обчислень (9)
.
Значить
Або
оскільки
то
Тому – сторонній розв’язок.
,
(11)
Розв’язки знайдені правильно.
|
Відповідь:
![]() ,
,
![]() ,
,

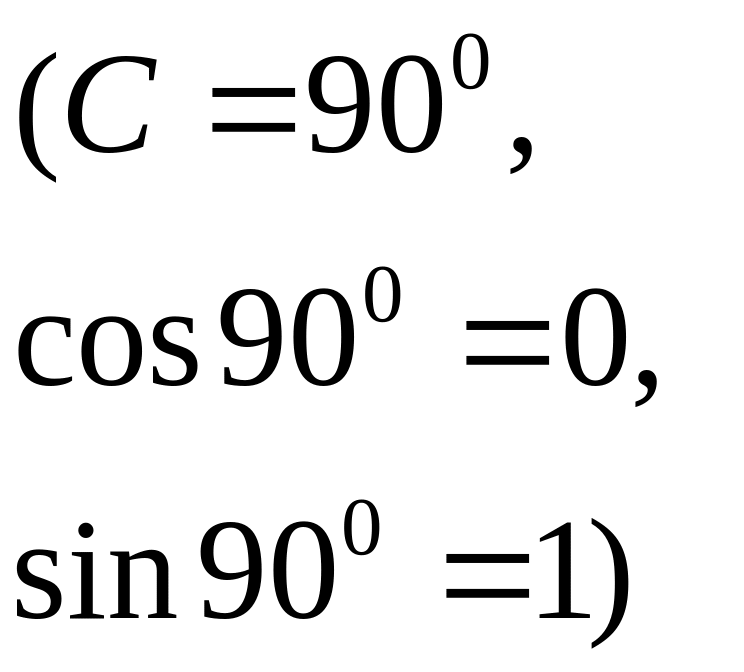

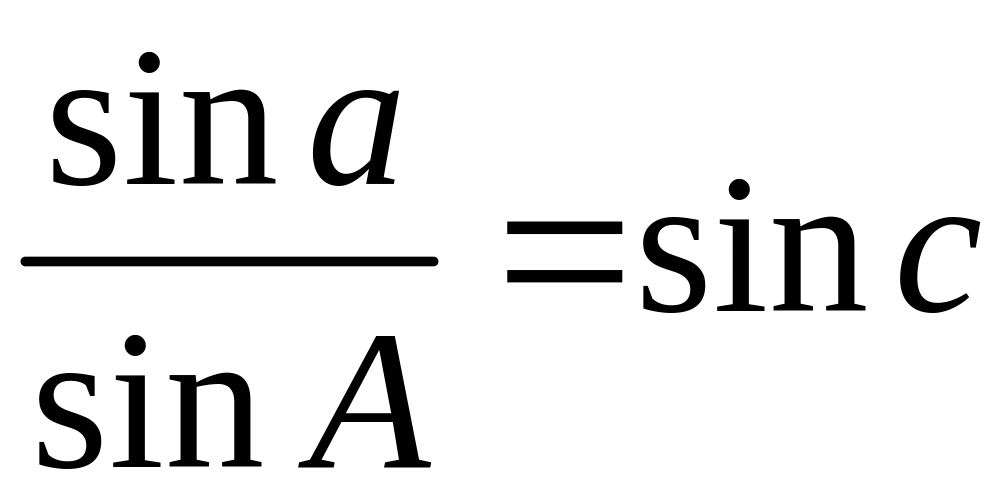 ,
тоді
,
тоді
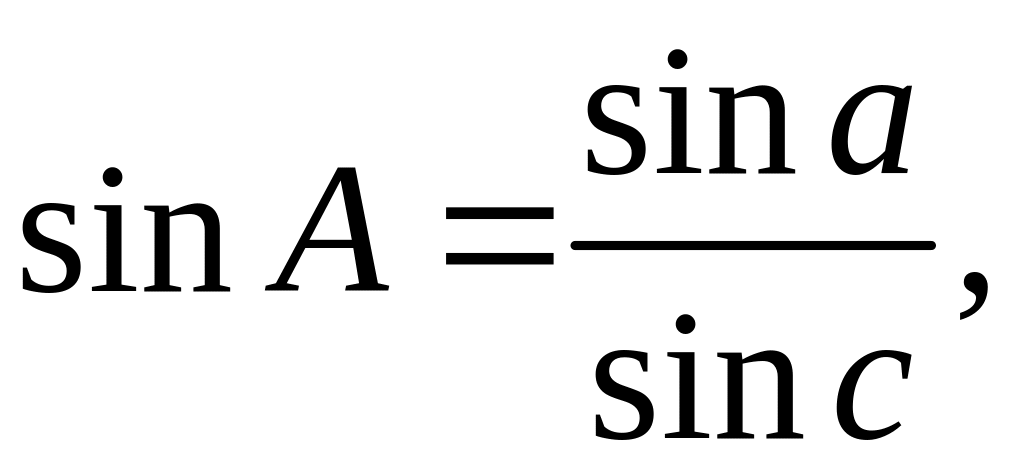
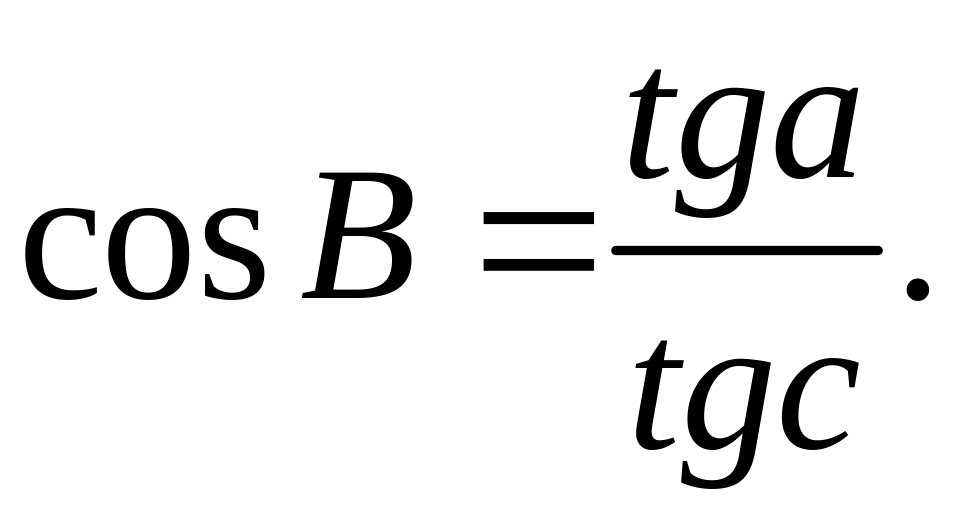
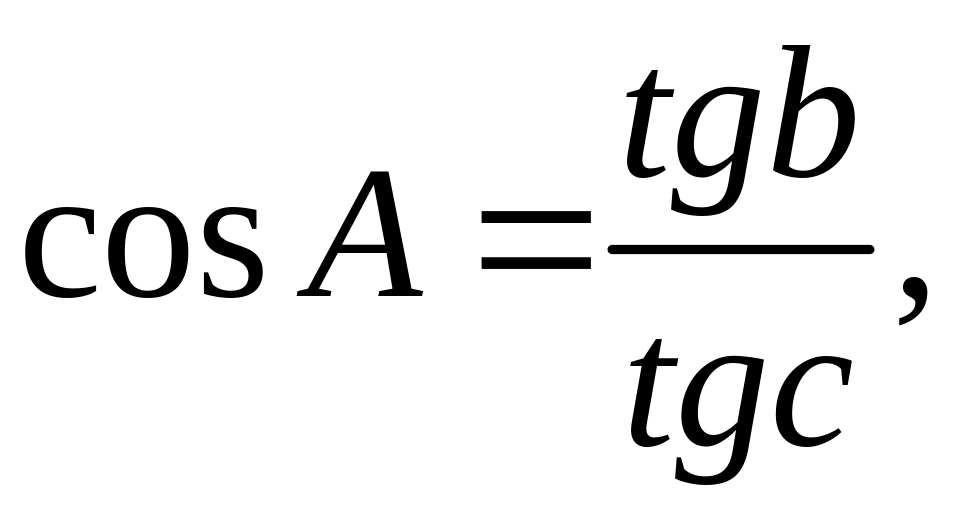
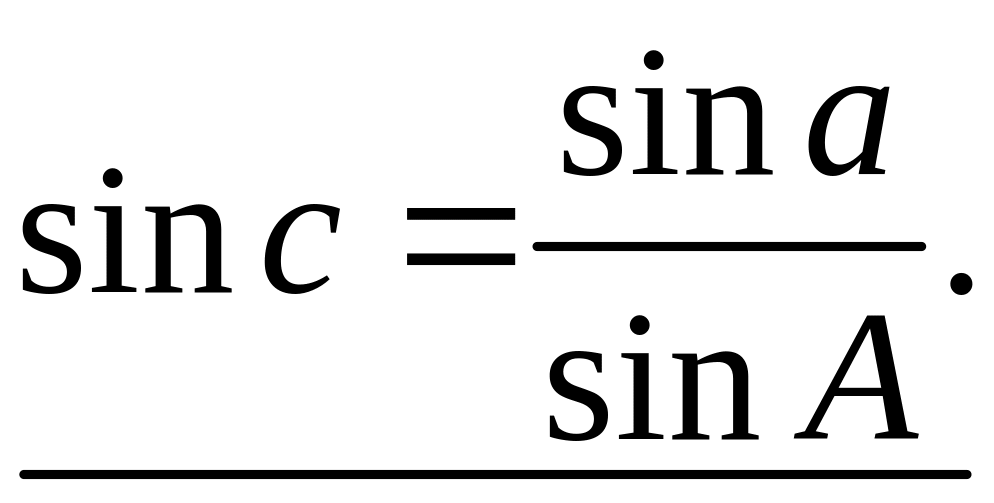
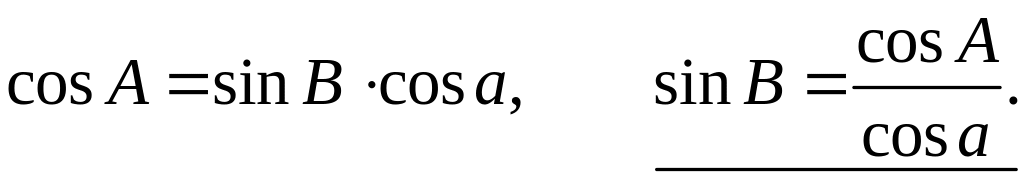
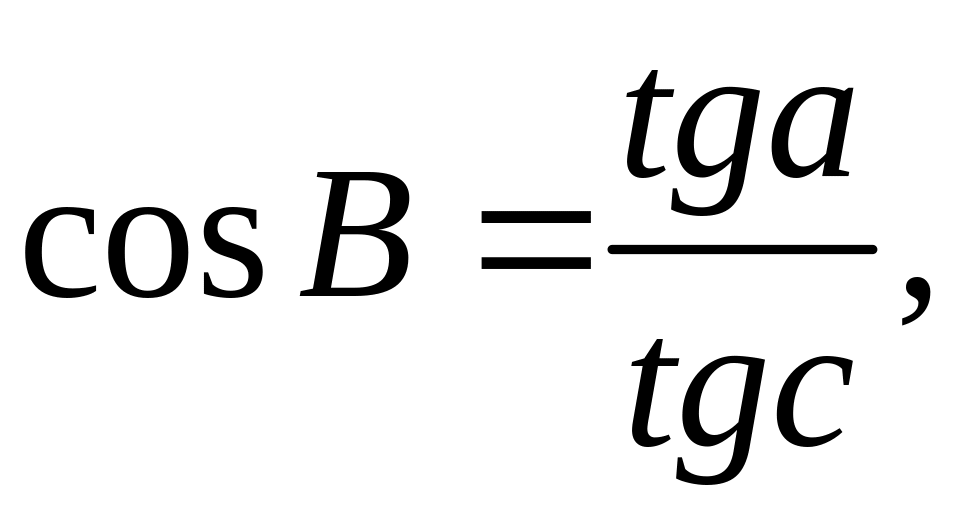
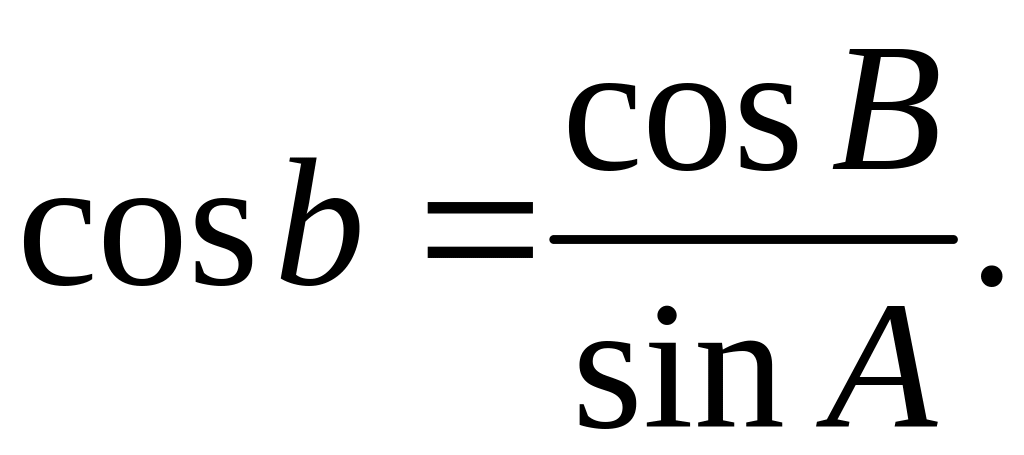
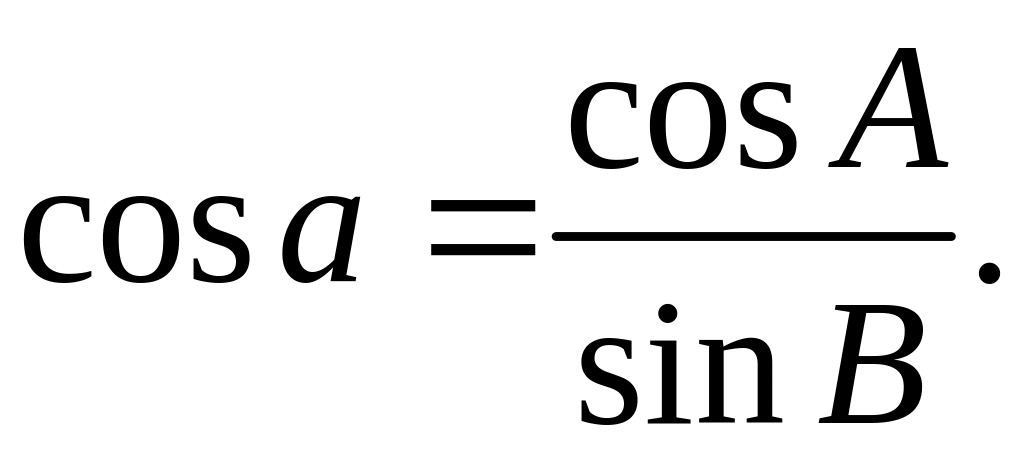
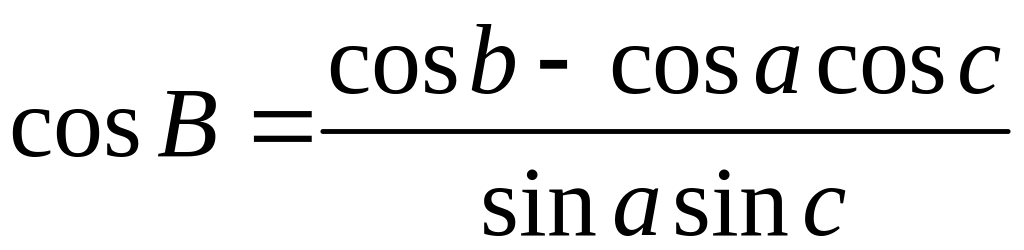 ,
,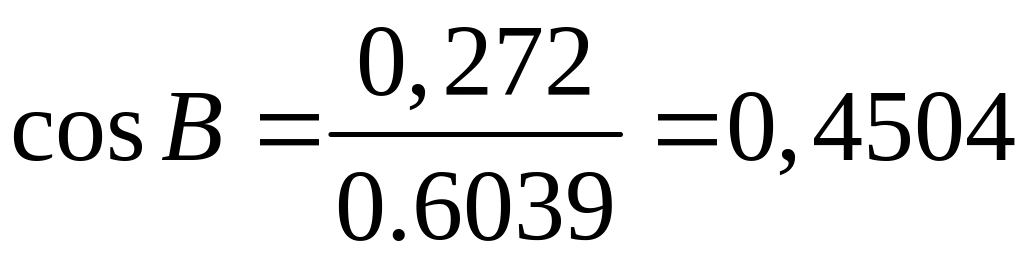 ,
,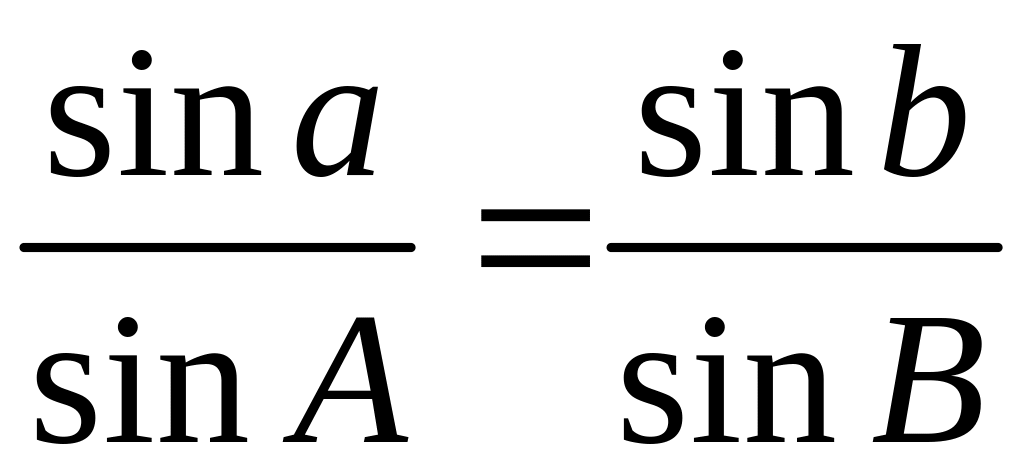 ,
звідки
,
звідки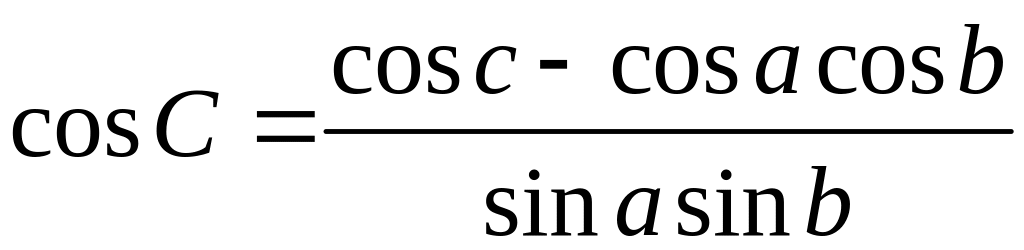 ,
,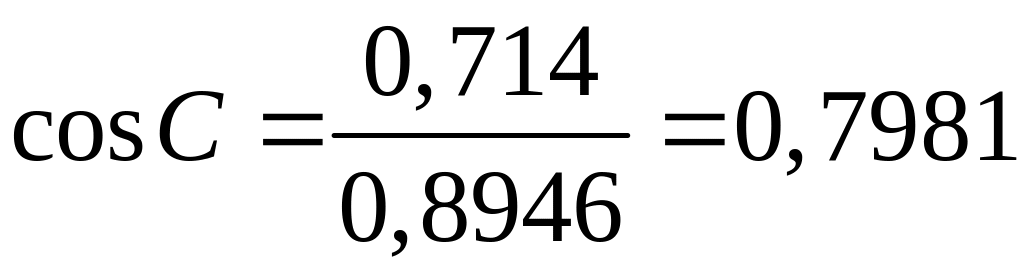 ,
,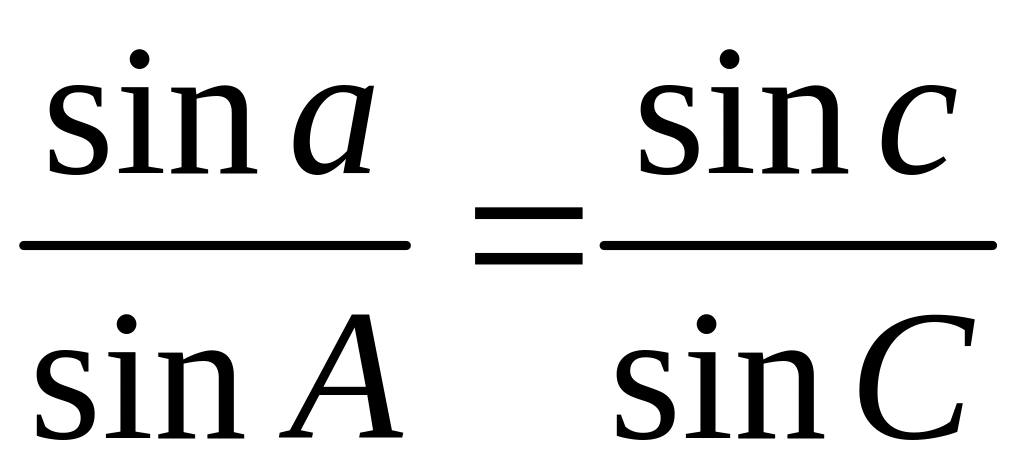 ,
звідки
,
звідки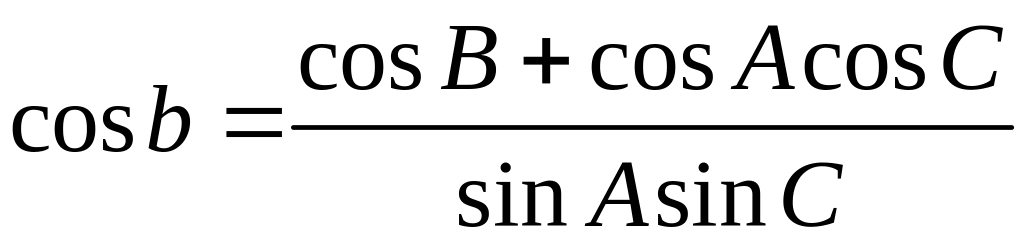 ,
,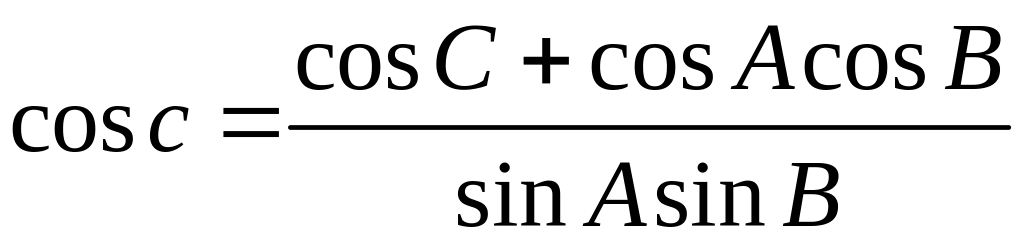
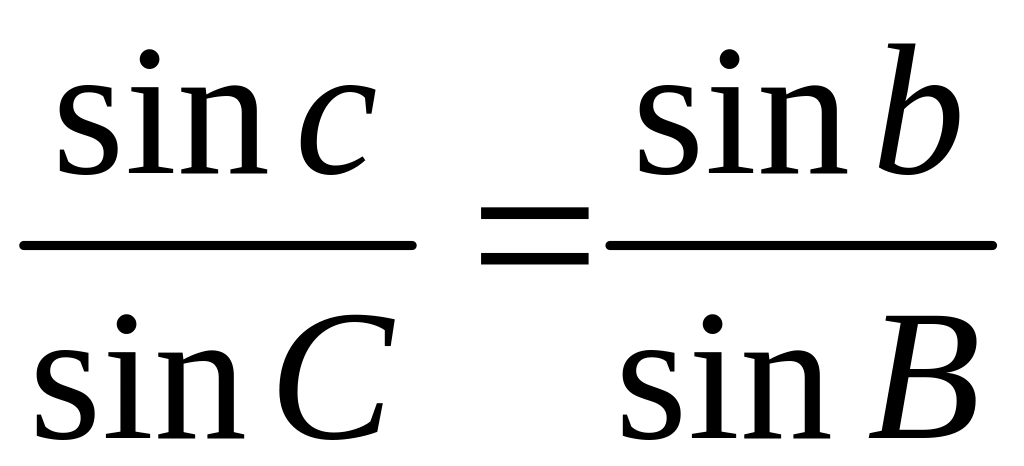
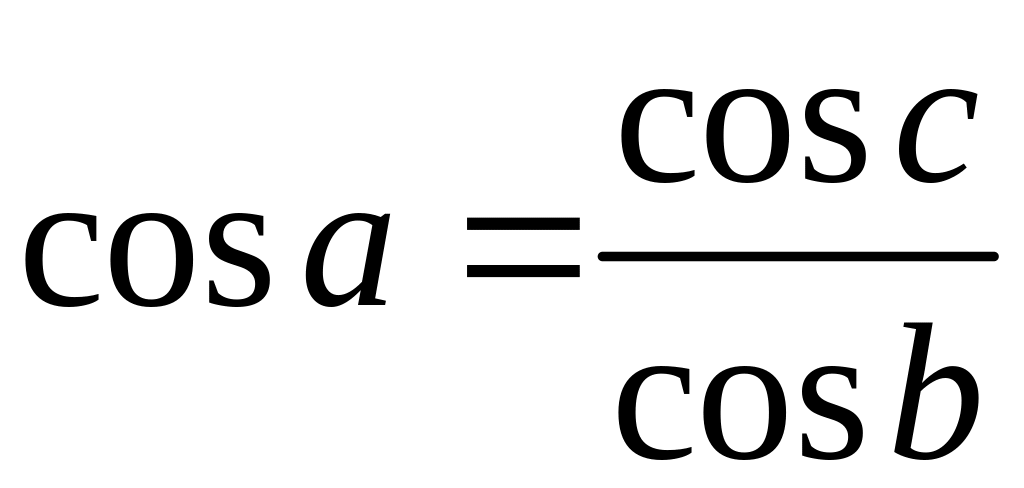 ,
,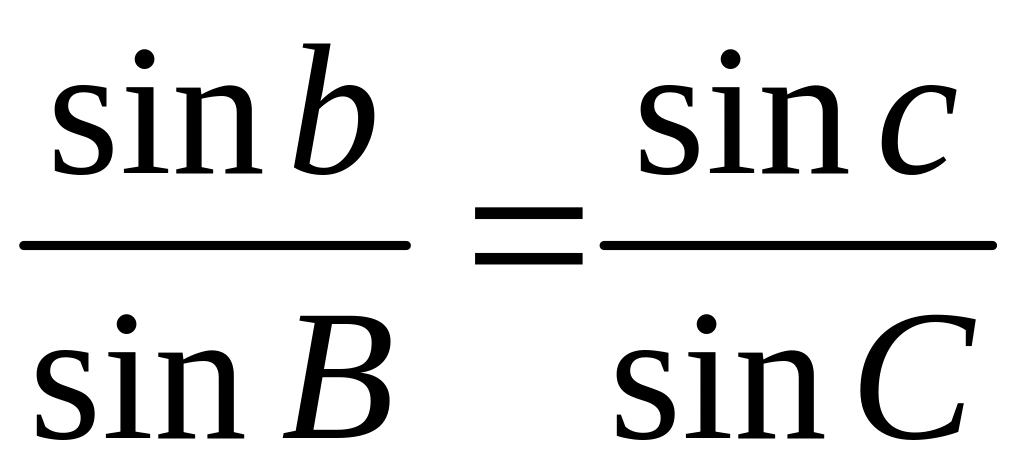 ,
,
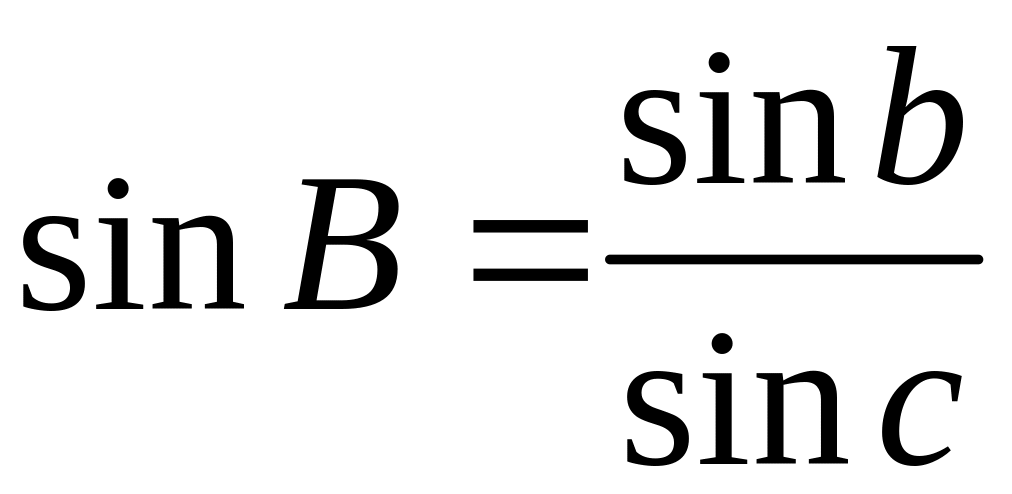 ,
,
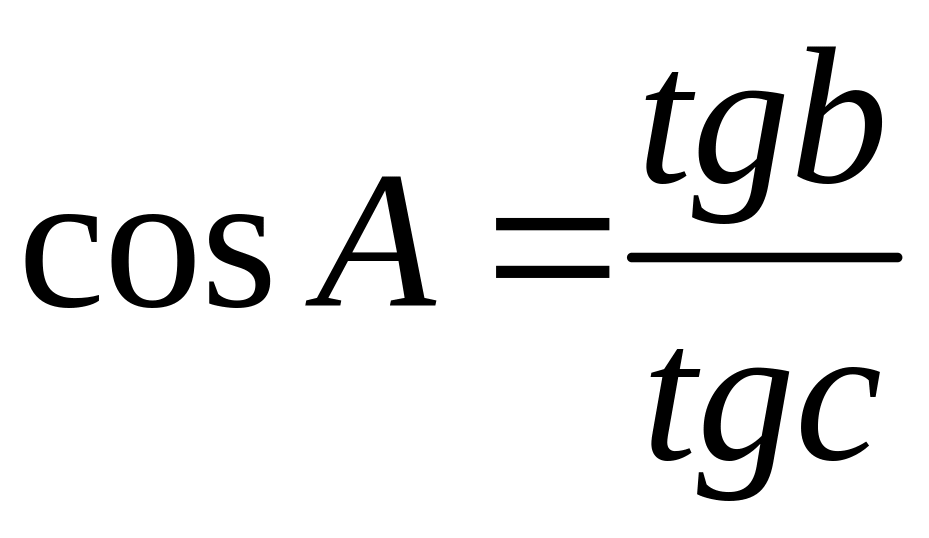 .
.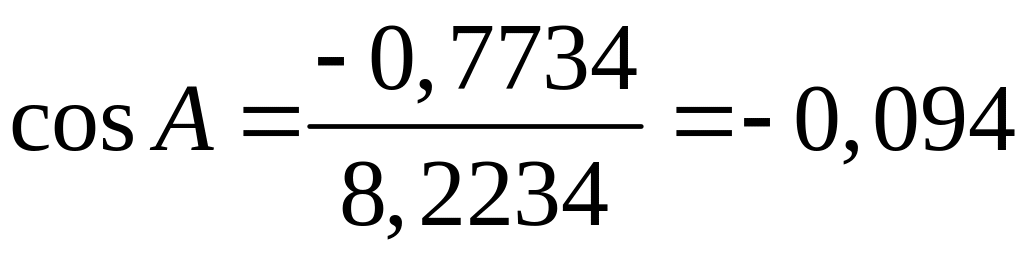
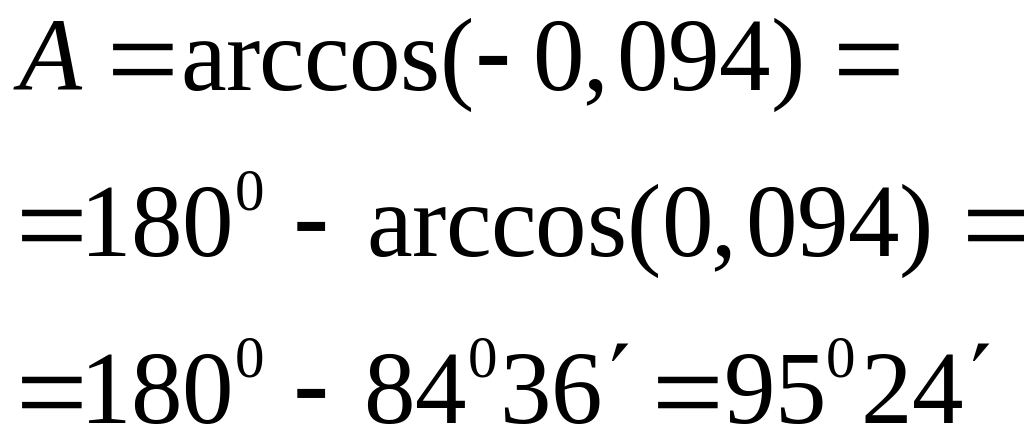
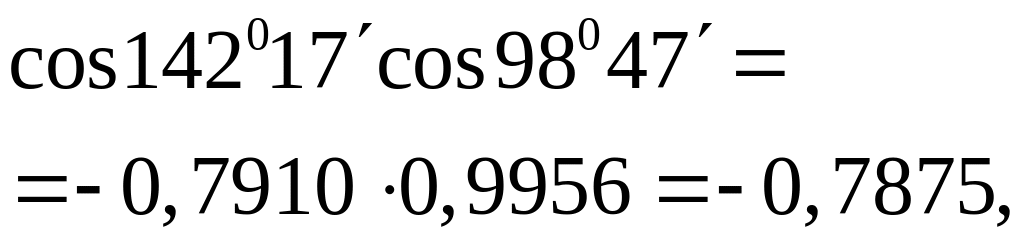
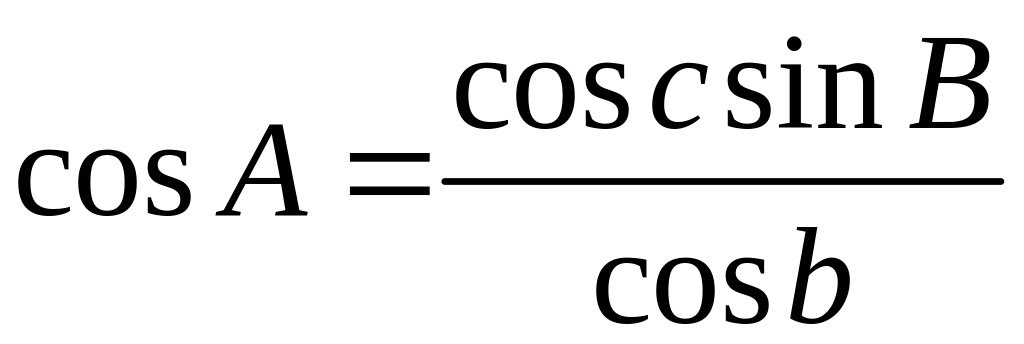
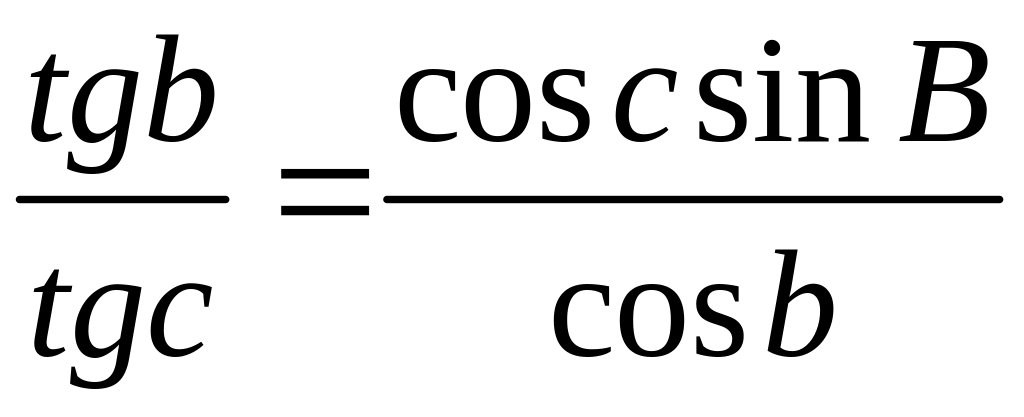 ,
,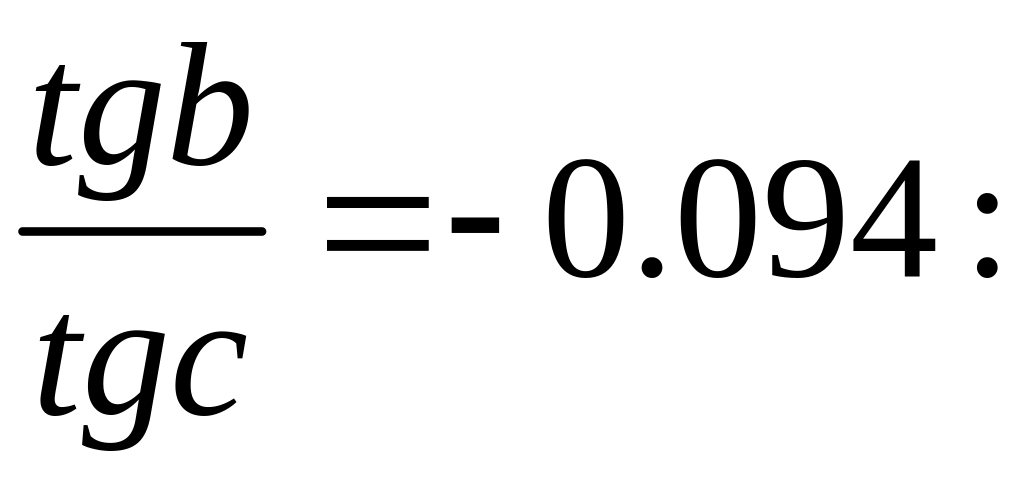
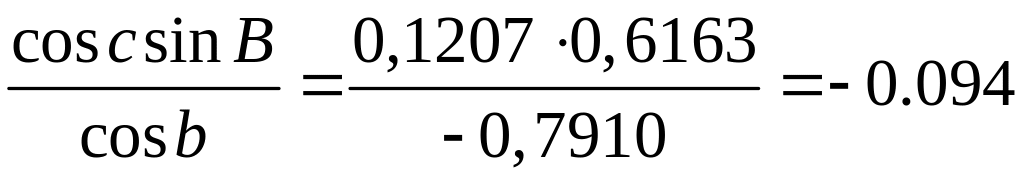 ;
;