6. Побудова трикутника на сфері:

а) за трьома сторонами; б) за трьома кутами

а). Побудувати на сфері трикутник за трьома сторонами та , якщо , .

Розв'язання.

Перевіримо, чи існує сферичний трикутник з такими сторонами. Відомо, що для існування сферичного трикутника повинні виконуватись наступні умови:

а) , ;

б) , ;

в) , ;

г) . .

Умови а-г виконані, значить сферичний трикутник може існувати..

Хід побудови.

1. Вибираємо довільний радіус сфери.

2. Будуємо коло, що відповідає колу великого круга на сфері (рис.7а).

Нехай О₁ А₁ = R

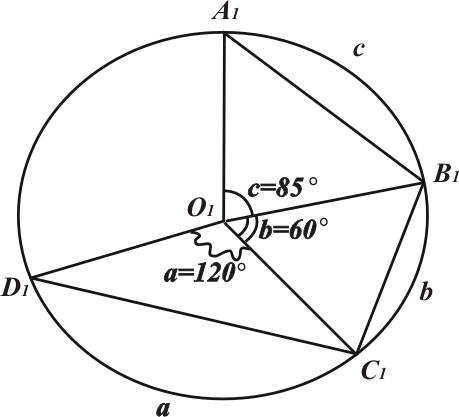
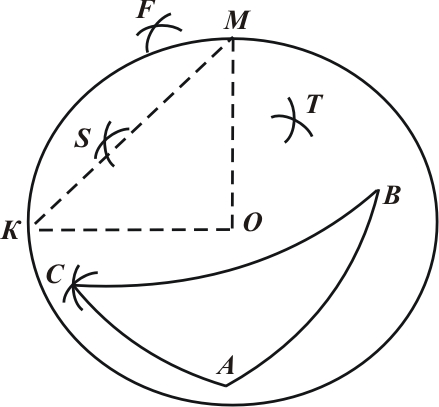
а) б)

Рис. 7

3. Від радіуса О₁ А₁ відкладаємо центральні кути , , та з'єднуємо між собою хордами точки та , та , С₁ та D₁.

4. Будуємо сферу радіуса . (рис. 7б)

5. Вимірявши циркулем хорду дуги с (рис. 7а), відмітимо на сфері дві точки та , відстань між якими . (Дуга великого кола дорівнює дузі с, так як рівним хордам одного й того ж кола відповідають рівні центральні кути).

6. Опишемо на сфері радіусом коло з центром в т. та радіусом - коло з центром в т. . - точка перетину цих кіл.

7. Будуємо полюси S,T,F відповідно дуг АВ, АС, ВС .

8. На сфері будуємо дуги великих кіл, що проходять через точки А та В, А та С, В та С . Одержимо сферичний трикутник АВС.

б). Побудувати сферичний трикутник за трьома кутами А, В та С.

План побудови.

1 Перевірити, чи існує сферичний трикутник з такими кутами.

2. Обчислити сторони , , трикутника , полярного до трикутника .

3. Побудувати трикутник за трьома сторонами , , .

4. Побудувати полюси дуг А₁В₁, А₁С₁, В₁С₁. Це будуть точки С, В та А – вершини шуканого трикутника..

5. Побудувати дуги великих кіл, які проходять через точки ; ; . Трикутник шуканий.

7. Довести нерівності:

а) ; б) .

Іv. Питання для самоконтролю.

1. Назвати поняття, які були введені в лекції. Дати їх визначення.

2. Що називається сферичним трикутником?

3. Що є мірою кутів (сторін) сферичного трикутника?

4. Користуючись зображенням на сфері трьох великих кіл (рис.5), назвати:

а) суміжні сферичні трикутники;

б) симетричні сферичні трикутники;

в) сферичний перпендикуляр до дуги, яку називає викладач;

г) чи є серед сферичних трикутників, зображених на сфері, прямокутні?

5. Сформулювати властивості кутів і сторін суміжних та симетричних трикутників.

6. Сформулювати умови існування косокутних ( прямокутних) сферичних трикутників?

7. Що можна сказати про величину третьої сторони сферичного трикутника, якщо а=130⁰, b=100⁰ ?

8. Які сферичні трикутники називають взаємно полярними?

9. Записати співвідношення між сторонами і кутами взаємно полярних трикутників.

10. Трикутники та _--взаємно полярні. Знайти: а) сторони трикутника , якщо , , ;

б) сферичний надлишок.

11. Довести, що .

12. Записати формулу для обчислення площі сферичного трикутника.

13. Обчислити площу сферичного трикутника АВС, якщо: а) А=132⁰, В=74⁰, С=100⁰ ; б) .

14. Сформулювати план побудови трикутника на сфері: а) за трьома сторонами; б) за трьома кутами.

V. Література.

1. Андронов И.К., Окунев А.К., Курс тригонометрии « Пособие для учителей» - М: Просвещения , 1967,– 648 с., (488-494 с.).

2. Волынский Б.А. Сферическая тригонометрия – М.Наука 1977,– 136 с.,

(25-34 с.).

3. Кранц П., Сферическая тригонометрия – М. 2007,– 93 с. (10-15, 79-81 с.).

Лекції 4-5. Тема: Основні формули сферичної тригонометрії

І. План лекції.

1. Теорема синусів.

2. Теореми косинусів сторін сферичного трикутника.

3. Теореми косинусів кутів сферичного трикутника.

4. Наслідки з теорем синусів та косинусів.

ІІ. Основні типи задач

1. Розпізнавати записані співвідношення між елементами сферичного трикутника.

2. Читати (змістовно) записану тотожність.

3. Формулювати критерії застосування кожної тотожності.

4. Одержувати з однієї тотожності дві інші за допомогою кругової перестановки букв.

ІІІ. Короткі теоретичні відомості.