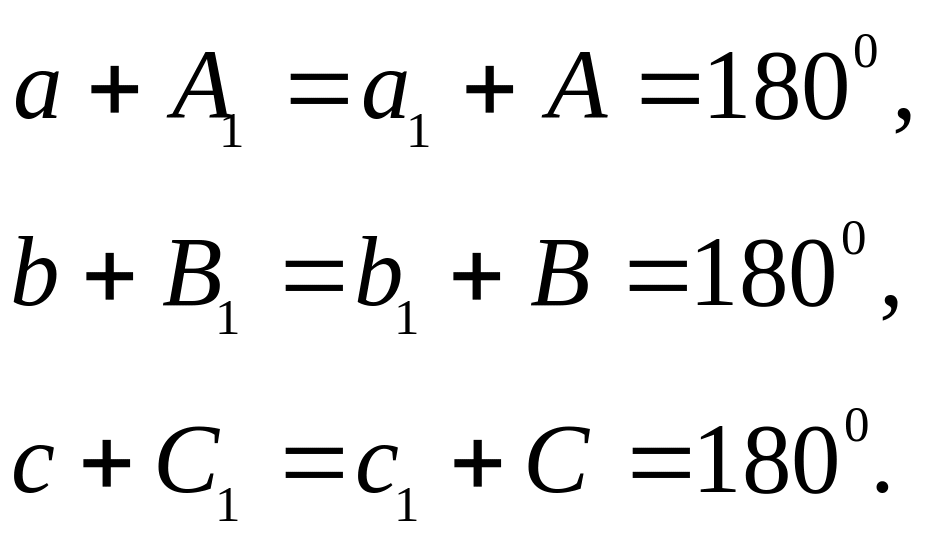І. План лекції

1. Поняття сферичного трикутника, його елементи. Вимірювання сторін і кутів сферичного трикутника.

2. Суміжні та симетричні трикутники, їх властивості.

3. Умови існування сферичного трикутника.

4. Взаємно полярні трикутники та їх властивості.

5. Площа і сума кутів сферичного трикутника.

6. Побудова трикутника на сфері: а) за трьома сторонами; б) за трьома кутами.

7. Доведення властивостей кутів сферичного трикутника.

Іі. Основні типи задач.

1. Розпізнавання на сфері суміжних та симетричних трикутників.

2. Встановлення:

а) існування сферичного трикутника із зазначеними мірами його

сторін (кутів);

б) межі зміни третьої сторони, якщо відомі міри двох інших;

3. Доведення властивостей кутів (сторін) сферичного трикутника.

4. Обчислення площі сферичного трикутника та двокутника.

5. Знаходження сферичного надлишку.

6. Доведення нерівностей, що характеризують умови існування сферичного трикутника.

7. Побудова трикутника на сфері: а) за трьома сторонами; б) за трьома кутами.

Ііі. Короткі теоретичні відомості.

1. Поняття сферичного трикутника, його елементи. Вимірювання сторін і кутів сферичного трикутника

Сферичним трикутником називають частину поверхні сфери, обмежену дугами трьох великих кіл. Точки перетину великих кіл називають вершинами сферичного трикутника і позначають великими літерами (рис.5).

Під кутами сферичного трикутника розуміють лінійні кути двогранних кутів, утворених площинами великих кіл, які в перетині зі сферою утворюють сферичний трикутник. Дуги, заключені між двома вершинами, називають сторонами сферичного трикутника. Вершини позначають великими, а сторони однойменними малими літерами.

Мірою сторони є центральний кут, утворений радіусами сфери, проведеними в вершини трикутника.

2. Суміжні та симетричні трикутники, їх властивості

Два трикутники, що мають спільну сторону, називають суміжними. Наприклад: трикутники АВС та АВС₁; АВС та А₁ВС; АВС та АВ₁С. Сторони суміжних трикутників, що не є спільними з сторонами трикутника АВС, є доповненнями до 180⁰ його сторін, розміщених на одному великому колі. Наприклад: трикутники АВС і АВ₁С - суміжні.

ﮞ ВС + ﮞ В₁С = 180⁰, ﮞ АВ + ﮞ АВ₁= 180⁰ (рис.5)

Рис 5

Два кінці одного і того ж діаметра сфери називають відповідними точками.

Два трикутники, вершини яких є відповідними точками, називають відповідними або симетричними трикутниками. Наприклад, трикутники

АВС і А₁В₁С₁, А₁ВС₁ і АВ₁С, та ін.

Симетричні трикутники мають рівні площі (є рівновеликими).

Відповідні сторони і кути симетричних трикутників (наприклад АВС та А₁В₁С₁) рівні між собою.

Таблиця 2

3. Умови існування сферичного трикутника (1) , , , , , , (2) (3) (4) (5) (6) (7) Якщо сума двох кутів сферичного трикутника більша, дорівнює або менша , то і сума протилежних їм сторін відповідно більша, дорівнює або менша . (8) Якщо різниця двох сторін сферичного трикутника більша, дорівнює або менша нуля, то і різниця протилежних їм кутів відповідно більша, дорівнює або менша нуля. Умови існування прямокутного сферичного трикутника (1)-(8) (9) Число сторін, більших , має бути парним, а менших - непарним. (10) Катет і протилежний йому кут завжди лежать в одній чверті круга.

4 .. Взаємно полярні трикутники та їх властивості. Два сферичні трикутники, що лежать на одній і тій же сфері, називаються полярними, якщо вершини одного з них є полюсами сторін другого Співвідношення між сторонами і кутами взаємно полярних сферичних трикутників і (рис.6) (5)

Рис.6

Периметр полярного сферичного трикутника А₁В₁С₁ можна подати у вигляді 2р₁ = а₁ + в₁ + с₁ = 180⁰ – А + 180⁰ – В + 180⁰ – С = 360⁰ – (А+В+С–180⁰) = =360⁰ – ε = 2π – ε.

5. Площа і сума кутів сферичного трикутника.

Площу сферичного трикутника обчислюють за формулами

(1) , де R-радіус сфери;

(2) , де - сферичний надлишок. (3)

Сума кутів сферичного трикутника . (4).