3. Задачі з астрономії та їх розв’язування

Задача. З астрономічного довідника відомо, що 18 травня схилення Сонця . Де воно буде знаходитись у цей день через 2 год 45 хв після верхньої кульмінації в Москві?

Розв’язання:

Для розв’язання задачі треба знайти координати у горизонтальній системі координат. Нехай у момент верхньої кульмінації Сонце знаходиться в точці Х₁ небесного меридіана. У цей час у Москві буде опівдні. За 2 год 45хв коло схилення Сонця повернеться на захід на кут і Сонце займе на небесній сфері положення Х.

Запишемо координати точки Х у горизонтальній та екваторіальній системах координат.

Х , де , ;

, де . Крім того - широта місця спостереження, тобто широта Москви, .

Розглянемо сферичний трикутник PXZ (його називають паралактичним, його вершинами є зеніт Z, полюс світу Р і світило Х).

, , , .

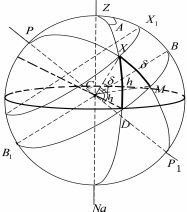
Рис. 17

Запишемо теорему косинусів для сторони ZX сферичного трикутника PZX.

,

тобто , звідки Одержали , звідки - висота Сонця.

. Запишемо теорему косинусів для сторони PX:

,

.

Звідки , тобто , звідки .

Таким чином, висота Сонця дорівнює , а азимут дорівнює . Тобто Сонце знаходиться у напрямі на південний захід на . Це записують так: .

IV. Питання для самоконтролю.

1. Що називають небесною сферою?

2. Чи є радіус небесної сфери сталою величиною? Чому?

3. Дати означення:

а) осі земної кулі та осі світу;

б) полюсів земної кулі та полюсів світу;

в) екватора земної кулі та небесного екватора;

д) меридіана на земній кулі та небесного меридіана;

4. Як визначають положення точки на небесній сфері:

а) у горизонтальній системі координат?

б) в екваторіальній системі координат?

5. Вказати аналоги у визначенні географічних координат точки та екваторіальних координат світила.

V. Література

1. Андронов И.К., Окунев А.К., Курс тригонометрии „ Пособие для учителей ”- М: Просвещение , 1967, – 648с. (524-538 с.).

2. Кранц П., Сферическая тригонометрия – М. 2007, – 93с. (33 - 48 с.).

3. Куликов К.А., Курс сферической астрономии – Изд-во Наука, - М. 1969- 216 с. (22-25 с.)

2. Зразки завдань для закріплення лекційного матеріалу:

До лекції 1. Точки і кола, дуги і кути на сфері. Сферичний двокутник

1. Зобразити на сфері довільне коло великого радіуса. Провести до нього сферичний перпендикуляр. Відповідь обґрунтувати.

2. Зобразити на сфері два великі кола, що перетинаються. Записати:

а) вертикальні кути; б) суміжні кути.

3. Обчислити площу сферичного двокутника якщо: а) R=6370 км, а сферичний кут дорівнює ( , , ).

4. Обчислити довжину дуги радіуса , градусна міра якої становить: , , , .

5. Відмітити на сфері даного радіуса дві довільні точки. Побудувати дугу великого кола, що проходить через ці точки.

6. Визначити дальність видимого горизонту з висоти ока спостерігача (наприклад, h=1,8 м), приймаючи радіус Землі, як кулі R=6370 км.

7. У місті А, яке знаходиться на 50 км від міста В, помітили на горизонті підняту над містом В повітряну кулю. Яка висота кулі в цей момент (R=6370 км).

8. Виразити у лінійних одиницях сферичну відстань, визначену в градусах: а) ; б) .

9. Виразити у градусній мірі сферичну відстань, визначену у лінійних одиницях: а) ; б) .

До лекцій 2-3. Сферичний трикутник.

1. Чи можна сферичний трикутник задати такими елементами? Відповідь обґрунтуйте.

а) , , ;

б) , , ;

в) , , ;

г) , , ;

д) , , ;

2. Чим відрізняються поняття: рівні і симетричні сферичні трикутники?

3. Довести, що: а) ; б) ;

в) ; г) .

4. Довести, що зовнішній кут сферичного трикутника менший суми двох внутрішніх кутів, з ним не суміжних, але більший за їх різницю.

5. Довести, що у сферичному прямокутному трикутнику число сторін більших , повинно бути парним, а менших – непарним.

До лекцій 4-5. Основні формули сферичної тригонометрії.

1. Вставити пропущені слова та словосполучення у наступних твердженнях:

а) теорему синусів доцільно використовувати, якщо дано … або … .

б) теорему косинуса сторони доцільно використовувати, якщо дано … або …

в) теорему косинуса кута доцільно використовувати, якщо дано … або … .

2. Яку кругову заміну букв слід використати, щоб з першої (другої, третьої) формули групи (4) одержати першу (другу, третю) формулу групи (4’).

3. Яку кругову заміну букв слід використати, щоб з першої (третьої, п’ятої) формули групи (5) одержати другу (четверту, шосту) формулу цієї ж групи.

4. Записати формули для груп (1) – (5), при умові, що .

5. Записати теорему Піфагора для сферичного трикутника, при умові, що:

а) , б) .

6. Чи може існувати прямокутний сферичний трикутник, у якого:

а) , , , ;

б) , , ;

с) , , , .

До лекції 6-7. Розв’язування сферичних трикутників.

1. Якими теоремами доцільно скористатись при розв’язуванні трикутника за:

а) трьома сторонами;

б) трьома кутами;

в) двома сторонами та кутом між ними;

2. Дано два кути сферичного трикутника:

а) , ; б) , .

Вибрати третій кут так, щоб сферичний трикутник існував (не існував).

3. Задані дві сторони сферичного трикутника:

а) , ; б) , .

Вибрати третю сторону так, щоб сферичний трикутник не існував (існував).

4. Перерахувати елементи сферичного трикутника, які входять у формули, що пов’язують між собою:

а) дві сторони і один кут;

б) дві сторони і два кути;

в) три кути і дві сторони.

Записати ці формули.

5. Розв’язати сферичні трикутники, у яких:

а) , , ;

б) , , ;

в) , , ;

г) , , ;

д) , , ;

е) , , .

До лекцій 8-9. Застосування сферичної тригонометрії в геодезії.

1. Зобразити пункти А і В, що задані географічними координатами:

А: , ;

В: , ;

2. Побудувати найкоротшу відстань між пунктами А і В.

3. Користуючись даними задачі 1, знайти міри дуг: AN, AS, BN, BS.

4. Довжина дуги великого кола земної кулі дорівнює кілометрів. Чому дорівнює центральний кут, що спирається на цю дугу, якщо:

а) ; б) .

5. Знайти довжину дуги великого кола земної кулі, радіус якої 6370км, на яку спирається центральний кут , якщо:

а) ; б) .

6. Знайти довготу пункту, у якому було опівдні, коли годинник, що показує час за Грінвічем, показував:

а) 12 год 15 хв; б) 13 год 04 хв; в) 14 год 05 хв;

г) 10 год 54 хв; д) 9 год 10 хв.

7. Знайти найкоротшу відстань між пунктами А і В, заданими географічними координатами, якщо:

а) А: , ;

В: , ;

б) А: , ;

В: , ;

в) А: , ;

В: , ;

До лекції 10. Застосування сферичної тригонометрії в астрономії.

1. Користуючись рис. 17, назвати паралактичний трикутник. Які співвідношення між його сторонами та висотою світила і його схиленням.

2. 16 травня схилення Сонця . Де воно знаходиться в цей день через 4 год. 15 хв. після його верхньої кульмінації в :

а) Одесі ( ); б) Марселі ( );

в) Лондоні ( ); г) Новоросійську ( ).

3. Знайти величину часового кута (кута ZPX), якщо з моменту проходження світила через нульовий меридіан пройшло:

а) 2 год 15 хв; б) 2 год 8 хв.