VII дискретные линейные системы автоматического регулирования

1.Классификация дискретных систем

В практике автоматического регулирования в последние годы на ряду с непрерывными САР широко применяют дискретные. Эти системы позволяют получить ряд новых существенных преимуществ, отличающих их от систем непрерывного регулирования. К этим преимуществам относятся:

1) Возможность осуществления многоточечного регулирования, т.е. возможность регулировать одним регулятором несколько объектов;

2) Возможность получения более благоприятного переходного процесса в случае наличия элементов запаздывания;

3) Возможность получения системы с бесконечно большой степенью устойчивости, в которой процесс регулирования заканчивается за конечное число интервалов регулирования.

К дискретным относятся системы, в состав которых входит хотя бы один элемент дискретного действия, преобразующий непрерывный входной сигнал в последовательность импульсов или квантованных сигналов.

Функциональную схему дискретной системы (рис.1) можно представить состоящей из дискретного элемента ДЭ и непрерывной части НЧ, куда входят НЧ1 и НЧ2.

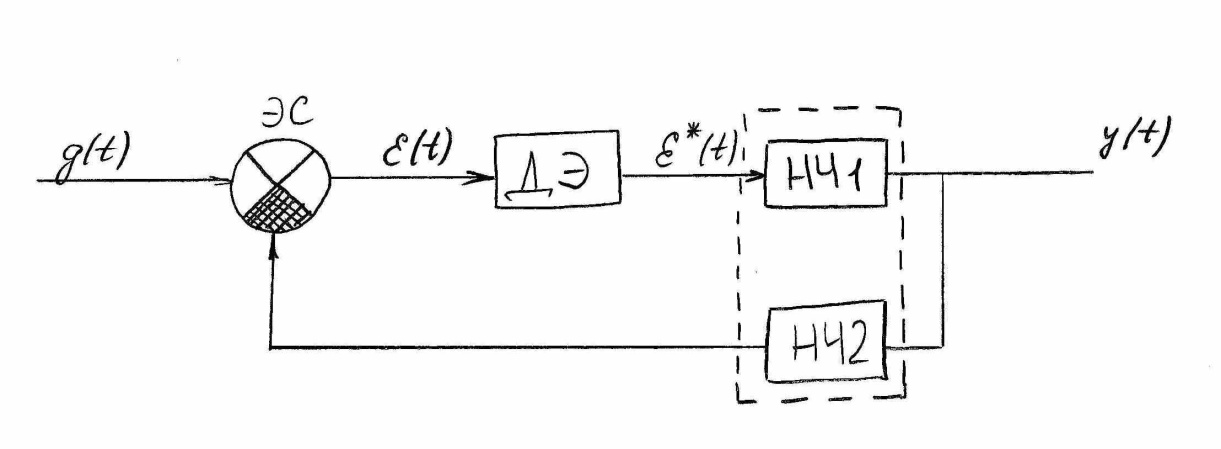
Рисунок 1

В системе последовательность импульсов с выхода ДЭ поступает на вход НЧ2 и, пройдя через неё, в следствии сглаживающих свойств НЧ1 преобразуется в непрерывный сигнал y(t). Последний пройдя через непрерывную ОС НЧ2 сравнивается в элементе сравнения со входным сигналом g(t). Полученный сигнал ошибки ε(t)=g(t)-y(t) поступает на вход ДЭ, который осуществляет квантование сигнала. Квантованием называется процесс преобразования непрерывного сигнала в дискретный. Различают 3 способа квантования: по уровню, по времени, по уровню и времени (рис. 2).

При квантовании по уровню (рис. 2а) непрерывный входной сигнал x(t) преобразуется в дискретный y(t) путём выделения значения непрерывного сигнала в моменты пересечения ими равноотстоящих уровней x₀, x₁, x₂… . Промежуток ∆x между уровнями называется интервалом квантования по уровню. Входной непрерывный сигнал x(t) пересекает заранее фиксированные уровни в произвольные моменты времени t₁,t₂, … , определяемые характером кривой x(t).

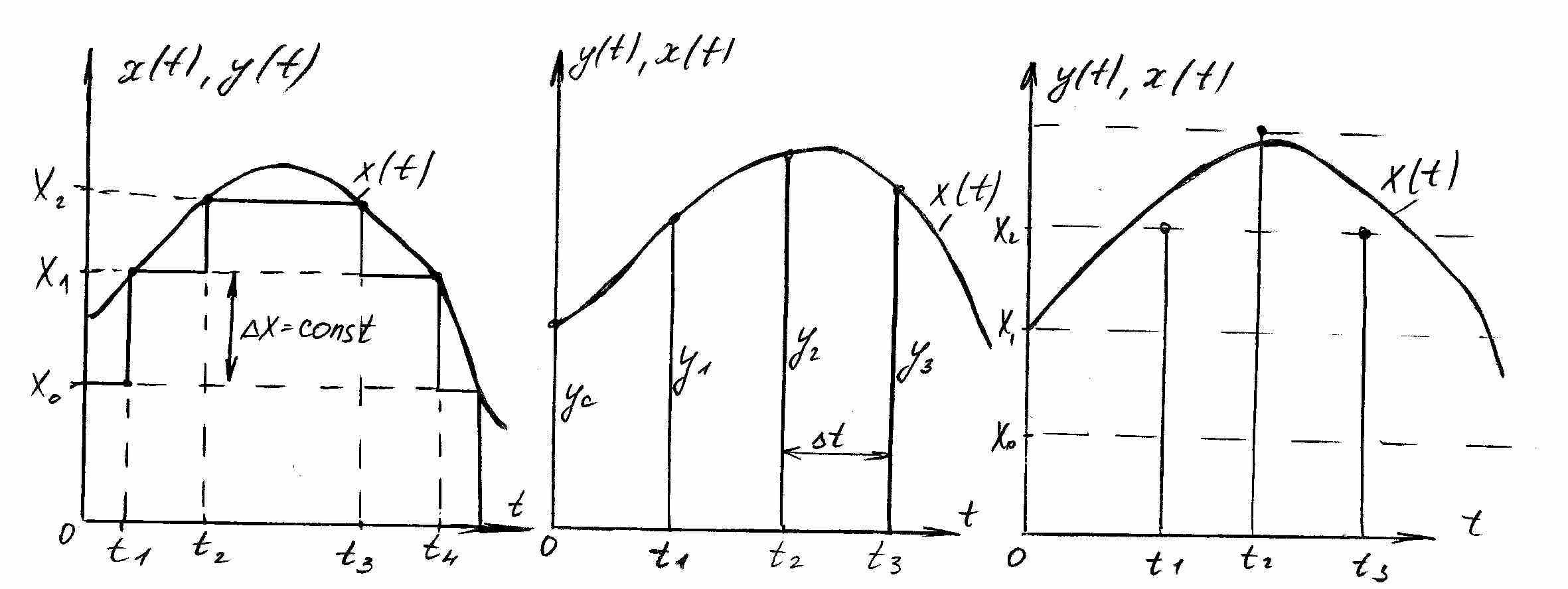
Рисунок 2

При квантовании по времени (рис. 2б) значение входного сигнала x(t) выделяется в виде дискретных выходных сигналов у₀, у₁, у₂, … произвольных уровней, определяемых характером кривой x(t) в фиксированные моменты времени t₁, t₂, … . Эти фиксированные моменты времени отстоят друг от друга на постоянную величину ∆t, называемую интервалом квантования по времени.

При одновременном квантовании по уровню и времени (рис. 2в) входной сигнал x(t) заменяется дискретным по уровню у₁, у₂, …, ближайшими к звеньям непрерывного входного сигнала в заранее фиксированные равноотстающие моменты времени t₁,t₂, … .

В зависимости от способа квантования непрерывного сигнала дискретные системы делятся на 3 вида: 1) релейные – при квантовании по уровню, 2) импульсные – при квантовании по времени, 3) цифровые – при квантовании по уровню и времени.

В практике автоматического регулирования широко распространены релейные и импульсные системы. Релейные можно рассматривать как нелинейные непрерывные системы с нелинейностью релейного типа. Поэтому к дискретным системам обычно относят лишь импульсные и цифровые.

Рисунок – Релейный тип

В импульсных системах под ДЭ понимается импульсный элемент ИЭ, который требует непрерывный входной сигнал в последовательность модулируемых импульсов. Поэтому ИЭ осуществляют квантование по времени и импульсную модуляцию можно рассматривать как импульсный модулятор. Импульсная модуляция заключается в изменении одного из параметров (этот параметр называют модулируемым) последовательности импульсов на выходе ИЭ по закону изменения непрерывного входного сигнала, который называется модулирующим.

Основными параметрами немодулируемой последовательности импульсов является (рис.3): ширина или амплитуда импульсов А, ширина или длительность импульсов γТ, где γ - скважность , изменяется от 0 до 1, расстояние между импульсами или период повторения импульсов Т, частота следования импульсов ω_и=2π/Т .

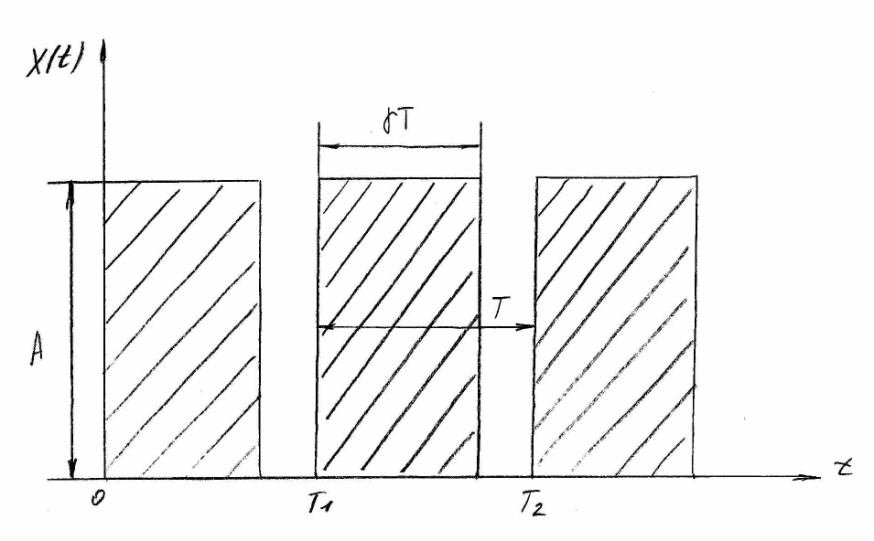
Рисунок 3

В зависимости от того, какой из параметров импульсов изменяется в зависимости от изменения входного сигнала, различают следующие виды импульсной модуляции:

1) Амплитудно – импульсная модуляция АИМ;

2) Широтно – импульсная модуляция ШИМ;

3) Время – импульсная модуляция ВИМ.

При подаче на вход ИЭ, осуществляющую АИМ (рис. 4а) непрерывного входного сигнала x(t) на выходе появляется последовательность импульсов, имеющая Т=const, γT=const. Амплитуда импульсов будет изменяться пропорционально значениям x(t) в момент появления импульса.

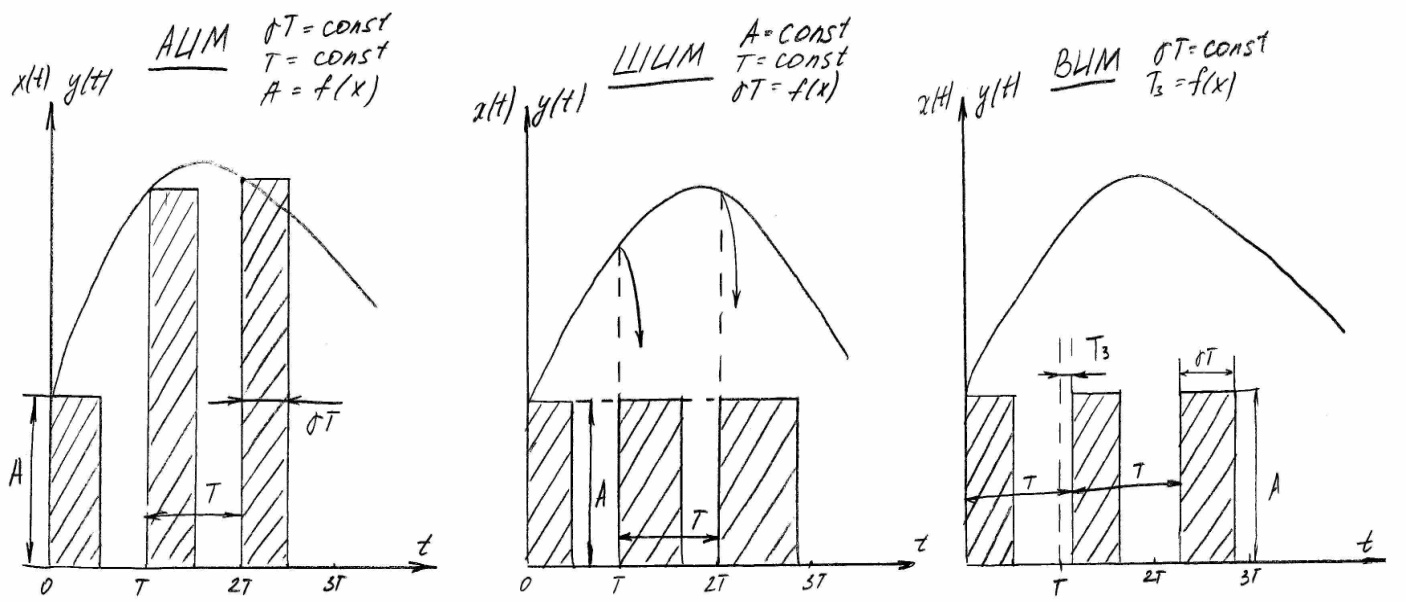
Рисунок 4

При подаче на вход ИЭ, осуществляющую ШИМ (рис. 4б) непрерывного входного сигнала x(t) на выходе появляется последовательность импульсов, имеющая Т=const, A=const, ширина импульсов γТ будет изменяться пропорционально значениям x(t) в момент появления импульса.

При подаче на вход ИЭ, осуществляющую ВИМ (рис. 4в) непрерывного входного сигнала x(t) на выходе появляется последовательность импульсов, имеющая γТ=const и A=const. В этом случае либо сдвиг по времени (по фазе) Т₃ относительно дискретных моментов квантования 0, Т, 2Т, … , либо частота импульсов ω_и=2π/Т, а следовательно в конечном итоге период повторения Т последовательности импульсов будет изменяться в соответствии с изменением входного сигнала x(t).

В зависимости от вида модуляций различают следующие автоматические системы:

- амплитудно-импульсная;

- широтно-импульсная;

- время-импульсная.

В практике регулирования технологических процессов наиболее распространены амплитудно-импульсные системы АИС. Поэтому в дальнейшем будем рассматривать только их.

К числу основных параметров ИЭ, кроме тех, которые характеризуют последовательность импульсов (А, Т, γТ), относятся:

- коэффициент усиления k_и;

- форма выходных импульсов s(t);

- статическая характеристика.

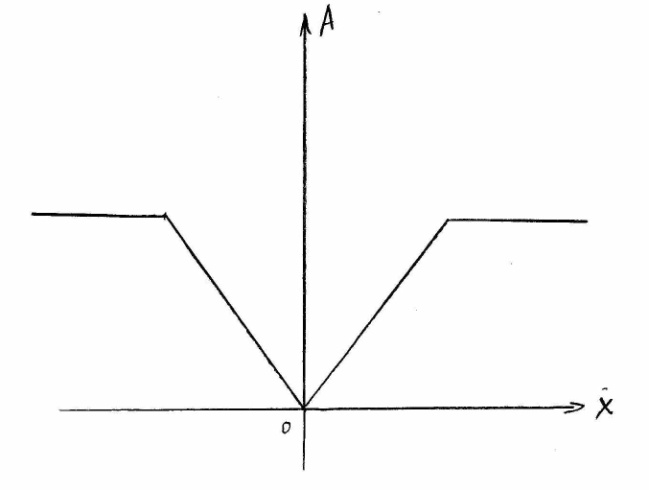
Статической характеристикой ИЭ называют зависимость величины модулируемого параметра (в случае АИМ это амплитуда А) последовательности выходных импульсов y(t) от соответствующих дискретных значений входного сигнала x(t). Эта характеристика может быть линейной или нелинейной. В зависимости от этого ИЭ может быть линейным или нелинейным.

По статической характеристике определяют коэффициент передачи ИЭ k_и, который представляет собой отношение амплитуды импульсов к дискретному значению непрерывного входного сигнала в соответствующий момент времени.

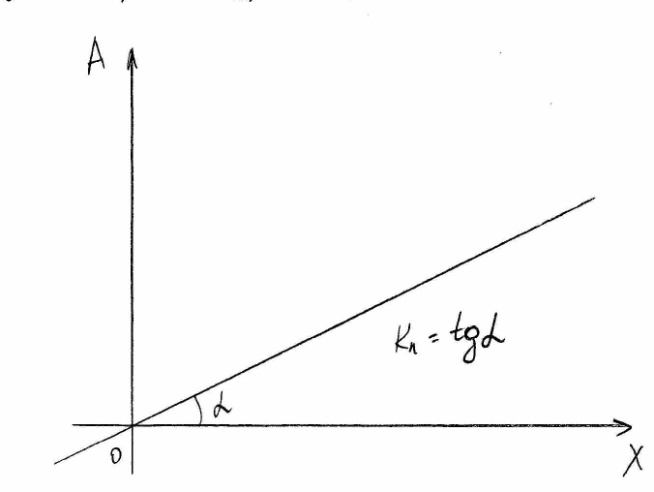
, где A- амплитудно импульсная составляющая входному сигналу в момент времени t=nT, Х-значение непрерывного входного сигнала в момент времени t=nT, n-переменный параметр, принимающий только целые значения 0,1,2,…

Форма выходных импульсов может быть разной: прямоугольной, треугольной, синусоидальной, экспоненциальной. Мы будем рассматривать АИС с прямоугольной формой. Форма импульсов описывается функцией формы S(t).

2. Математические основы теории импульсных систем.

Наличие в схеме АСИЭ определяет импульсный характер сигналов действующих в системе. Рабочие процессы, протекающие в таких системах, непосредственно связаны с воздействиями, передачей и преобразованием последовательности импульсов. Поэтому математический аппарат анализа импульсных систем имеет определенные особенности.

Рассмотрим кратко основные математические определения теории импульсных систем.

1. Решетчатая функция

Выходной сигнал ИЭ y(t) определяется значением входного сигнала x(t) в дискретные равноотносящееся моменты времени t=nT (рис 4(а) в 1) и не зависит от того какие значения принимает сигнал x(t) в промежутках между указанными моментами времени. Поэтому целесообразно при анализе ИС рассматривать значение непрерывной функции x(t) в дискретные равноотстоящие моменты времени 0,T,2T,… так как значение x(t) внутри интервалов Т не влияет на работу ИЭ

Функция, которая задана ординатами равными значению входного сигнала ИЭ x(t) в дискретные моменты времени nT, а между ними тождественно равны 0,назвают решетчатой. На рис. 1а показана непрерывная функция x(t), а на рис. 1б соответствующая ей решетчатая функция X(ИТ).

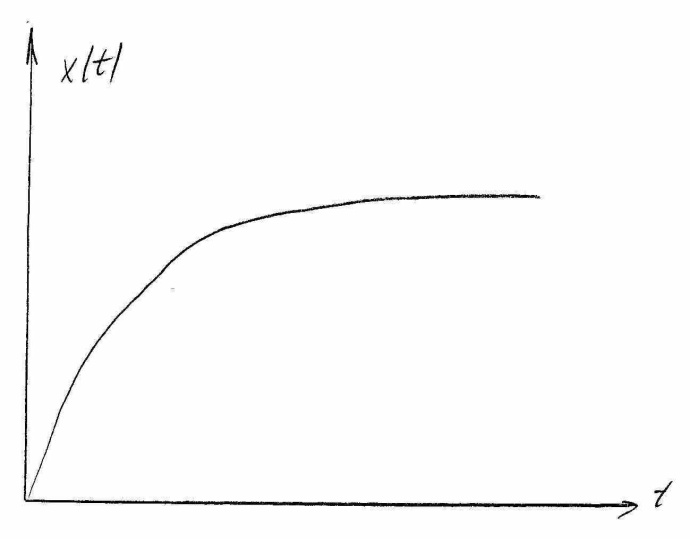
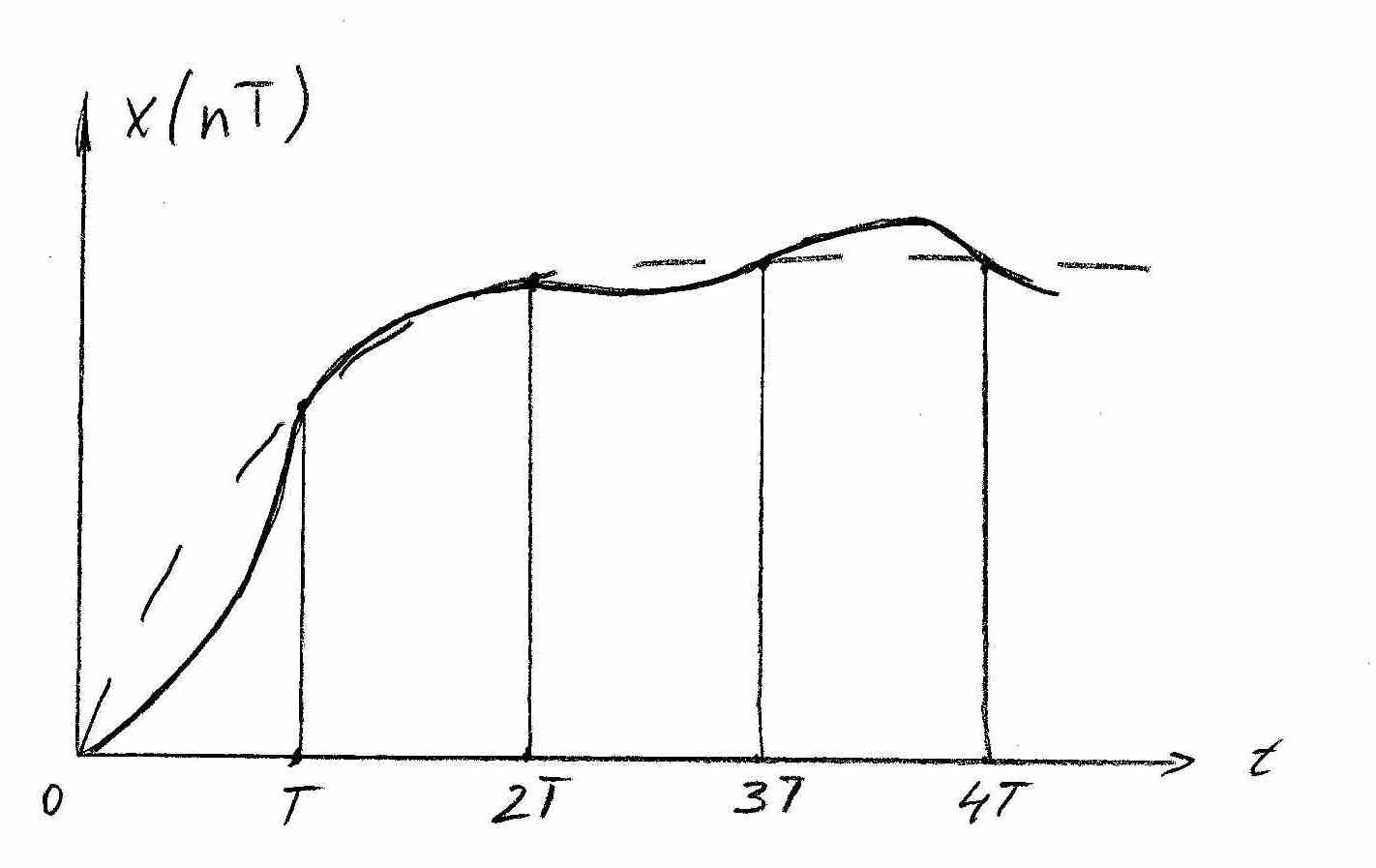
Рисунок 1

Аналитическое выражение решетчатой функции (поменяется????) если в выражение непрерывной функции поместить аргумент t=nT, те X(nT)=X(t).

При этом непрерывная функция x(t) является огибающей решетчатой функцией x(nT). Любой непрерывной функции X(t) соответствует только одна решетчатая функция x(nT), обратное утверждение неверно.

2. Дискретное преобразование Лапласа ДПЛ и z-преобразование

Играют в теории ИС такую же роль, как и обычное (непрерывное) ПЛ в теории непрерывных систем. Последнее, как известно, определяется по формуле

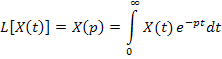
ДПЛ является функциональным преобразованием решетчатой функции x(nT) и определяется

(1)

Где D[X(nT)]- символ ДПЛ,X*(p)- дискретное изображение функции X(nT), сама функция X(nT)- оригинал, а p=y(gamma)+jw оператор преобразования в общем случае комплексная переменная.

Формула (1) позволяет решать прямую задачу ДПЛ для заданной решетчатой функции X(nT): найти ее дискретное изображение (прямое ДПЛ)

ПРИМЕР 1

Пусть решетчатая функция представляет собой единичный скачок, те X(nT)=1(nT), тогда ее дискретное изображение будет равно

=

Правая часть равенства представляет собой сумму бесконечно убывающей геометрической прогрессии, так как модуль ее знаменателя меньше 1

Т.о. дискретное изображение функции

ПРИМЕР 2

пусть дискретная функция экспонента ,тогда ее изображение

Тогда изображение этой функции будет иметь вид

Из полученных результатов и формулы 1 следует, что дискретное изображение X*(p) представляет собой рациональную функцию переменной e^pT. Поэтому для практического использования ДПЛ оказывается удобным ввести обозначение e^pT=z и рассматривать дискретное изображение как функцию новой переменной z. В связи с этим формула 1 принимает вид

(2)

Выражение 2 определяет прямое z-преобразование решетчатой функции X(nT). В этом выражении операция z-преобразования обозначена Z[X(nT)], а результат операции- дискретное изображение функции X(nT) обозначено X(z)

Таким образом, если известно ДПЛ решетчатой функции или X(nT), то для перехода к ее z-изображению достаточно произвести следующую подстановку

В соответствии с формулой 3 для примеров 1 и 2 будем иметь

Следует отметить, что в теории ИС используются как ДПЛ, так и z-преобразование. Однако последнему отдается большее предпочтение ввиду простоты записи и ряда преимуществ, которые будут рассматриваться далее. На практике используют z-преобразование аналогично использованию непрерывного ПЛ для непрерывных систем

ОСНОВНЫЕ ТЕОРЕМЫ Z-ПРЕОБРАЗОВАНИЯ

Ниже без доказательства приведены наиболее важные теоремы z-преобразования. Эти теоремы во многом аналогичны соответствующим теоремам обычного ПЛ.

Применение указанных теорем позволяет использовать при анализе импульсных систем терминологию и методы непрерывных систем.

А) теорема линейности

Если решетчатая функция X(nT) представляет собой линейную комбинацию функций X1(nT) и X2(nT),т.е X(nT)=Q1X1(nT)+Q2X2(nT),где Q1 и Q2-пост коэффициенты, то учитывая линейность операций z-преобразование можно записать

X(z)=Q1X1(z)+Q2X2(z)

Т.о. z-изображение линейной комбинации решетчатых функций равно линейной комбинации их изображений.

Б) теорема сдвига

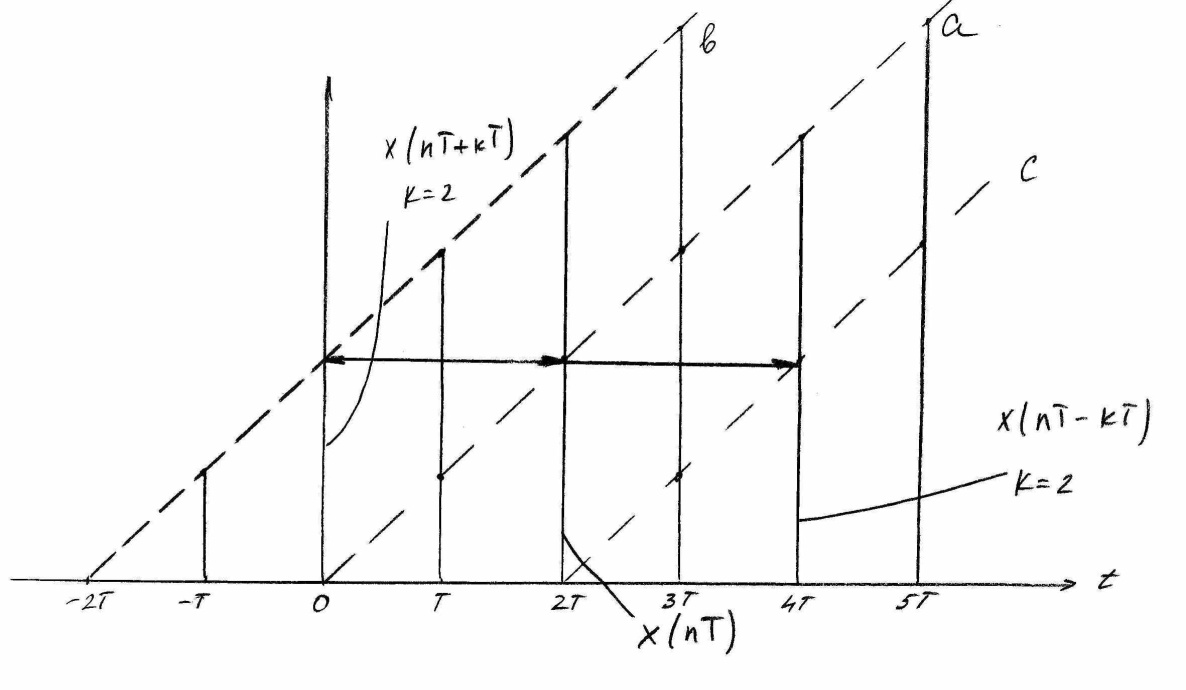
Рисунок

Теорема сдвига (смещения) позволяет по известному изображению X(z) дискретной функции X(nT) получить изображение смещения функции X(nT+-kT). Для ……….функции X(nT+kT), смещают влево относительно исходной на к - периодов влево, будем иметь

Эта формула справедлива в том случае, когда все начальные координаты исходной функции X(nT) до к-1 включительно равны 0: Х(0)=Х(Т)=Х(2Т)=…=Х(КТ-Т)=0. В противном случае изображение определяется по выражению:

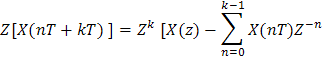
Изображение запаздывающей дискретной функции X(nT-kT), сдвинутой вправо на к интервалов (ее ординаты лежат на линии с) определяется . Эта формула справедлива, когда исходная функция Х(nT) тождественно равна 0 для всех значений k<0, т.е. когда выполняется равенство Х(-Т)=Х(-2Т)=…=Х(-kТ=0). Если условие не выполняется, то

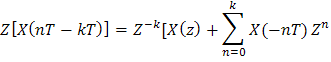
В) Теорема о конечном значении дискретной функции

Эта теорема позволяет определить установившееся значение дискретной функции X(nT), если известно ее изображение X(z)

Г) Теорема о начальном значении решетчатой функции

Пусть X(z) изображение дискретной функции, тогда

4) Методы определения дискретной функции по ее Z-изображению

Операция перехода от z-изображения к дискретной функции (оригиналу) получила название обратного z-преобразования, которое обозначается символом . Используют следующие методы определения дискретной функции по ее изображению

1. Определение оригинала с помощью разложения изображения на кратные дроби

При переходе от изображения к оригиналам часто может быть использована формула разложения аналогичная таковой в обычном ПЛ. От этого поступают следующим образом: от изображения X(z) переходят к изображению:

, которое представляют в виде суммы простейших дробей, чтобы обратные z-преобразования каждого слагаемого умноженного на z можно было бы найти в специальных таблицах z-преобразования. Поскольку обычно X(z) является дробно-рациональной функцией (см. примеры 1,2), то также будет в виде дроби. Обозначая числитель этой дроби B(z), а знаменатель A(z), будем иметь следующее разложение:

где r – число простых корней полинома A(z) и

Учитывая, что будем иметь ввиду

где ; применяя к этому изображению обратное z-пребразование получим:

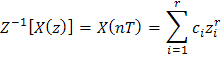
где

2. Определение оригинала путем разложения изображения в степенной ряд.

Сущность данного метода заключается в следующем: изображение X(z) разлагается в ряд по степеням , т.е. представляют в виде

Учитывая, что по определению z-пребразования решетчатой функции X(nT) изображения

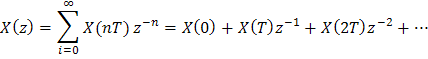
можно сделать вывод, что коэффициенты разложения равны соответственно значениям дискретной функции

Разложение X(z) в ряд обычно получают путем последовательного деления изображения X(z) на его знаменатель по правилам деления многочленов

5) Специальное z-преобразование

Ниже без доказательств приведены свойства специального я-преобразования:

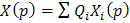1. , то

2. Если функция X(p) представляет собой произведение 2-х функций 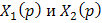, т.е. X(z)=Z[X(p)]=Z[ . При этом для определения X(z) необходимо предварительно вычислить произведение 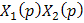, а затем подвергнуть полученный результат специальному z-преобразованию. Операцию Z[ символически записывают так = . Целесообразно в виду следующее свойство указанной операции Z[

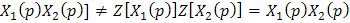
3. Z-изображение функций можно выносить за знак специального z-преобразования. Так, например, если Y(p)= , то Y(z)=Z[Y(p)]=Z[ ]=