6. Передаточные функции замкнутых систем.

1) Системы с импульсными элементами в цепи рассогласования с единичной обратной связью.

Характерной чертой замкнутых ИСАР является наличие ИЭ внутри замкнутого контура воздействий. Структурная схема простейшей импульсной замкнутой системы показана на рисунке 1 , где w(p) – передаточная функция звеньев прямой цепи, содержащая передаточную функцию ФЭ. для рассматриваемой схемы уравнения, связывающие между собой величины в изображениях по Лапласу имеют вид:

Рисунок 1

E(p) = G(p) – Y(p) Y(p) = E(z) w(z)

Выполняем 2-преобразование

E(z) = G(z) – Y(z) Y(p) = E(z) w(z)

Подставляя изображение Е(z) во второе уравнение и решая его, получаем дискретную передаточную функцию замкнутой системы

Подставляя 2-е уравнение в 1-е и решая его получаем передаточную функцию замкнутой системы по ошибке от задающего воздействия.

Для рассмотренного в §5 примера соответствующая функция будет иметь вид

2) Система с импульсным элементом в цепи и с произвольной непрерывной обратной связью.

Для этой схемы (рисунок 2) уравнения, связывающие между собой отдельные величины, в изображениях по Лапласу

Рисунок 2

E(p) = G(p) – Y(p) w₂(p) Y(p) = E(z) w₁(z)

Подставляя 2-е уравнение в 1-е получаем

E(p) = G(p) – E(z) w₁(z) w₂(p) откуда

E(z) = G(z) = E(z) w₁(z) w₂(p) тогда

изображение ошибки

где - передаточная функция по ошибке, учитывая что Y(z) = E(z) w₁(z) изображение выходного сигнала

3) Система с импульсным элементом на выходе прямой цепи регулирования

Для этой системы справедливы следующие соотношения (рисунок 3)

Рисунок 3

E(p) = G(p) – Y(z) w₂(p) Y(p) = E(p) w₁(p)

Подставляя 1-е уравнение во 2-е поучаем

Y(p) = G(p) w₁(p) – Y(z) w₁(z) w₂(p)

Y(z) = G(p) w₁(z) – Y(z) w₁ w₂(p)

Следовательно изображение выходной величины

Анализ рассмотренных случаев показывает, что для систем у которых ИЭ стоят на выходе сумматора можно найти дискретную передаточную функцию замкнутой системы, а для систем , у которых ИЭ стоит в другом месте, этого сделать нельзя.

7. устойчивость линейных импульсных систем.

Устойчивость является необходимым условием работоспособности любых САР, в том числе и импульсных.

Изложенные в главе 3 остальные определения устойчивости непрерывных систем применимы и к ИС, нос учетом ряда особенностей, присущих этим системам.

1) Необходимое и достаточное условия устойчивости.

Из теории непрерывных систем известно, что САР устойчива, если свободная составляющая переходного процесса y_св(t) с течением времени затухает, т.е.

Уточним данное условие применимо к ИС. Пусть динамические свойства ИСАР (разомкнутой или замкнутой) описываются дискретной передаточной функцией w(z), которая обычно представляет собой дробно-рациональную функцию оператора преобразования

где K(z) – характеристический полином степени k, корни которого z называются полюсами передаточной функции w(z); M(z) - полином числителя степени m, корни которого обращают w(z) в 0 и называются нулями передаточной функции w(z)

Z – изображение входного сигнала X(z) в большинстве случаев также является дробно-рациональной функцией параметра z.

, где

характеристический полином степени s, корни которого называются полюсами изображения входного сигнала.

Тогда Z-изображение выходного сигнала также является дробно-рациональной функцией параметра z

Для определения свободной составляющей переходного процесса найдем оригиналы изображений всех сигналов, т. е.дискретную функцию y(nT). При этом воспользуемся теоремой разложения (§2). Разложим Y(z) на простые дроби и в случае простых некратных полюсов будем иметь

где z_i – полюса передаточной функции w(z); z_j – полюса изображения входного сигнала X(z), а C_i и C_j – постоянные коэффициенты. Учитывая, что где получаем выражения для оригинала.

Отсюда следует, что переходный процесс имеет 2 составляющие : 1-я определяется полюсами z_i передаточной функции w(z) и отражает внутренние динамические свойства системы(свободное движение),т.е. является свободной (переходной) составляющей процесса регулирования; 2-ая составляющая определяется полюсами z_j изображения входного сигнала X(z) и отражает свойства системы в установившемся режиме, т.е является вынужденной (установившейся) составляющей процесса регулирования.

Импульсная САР является устойчивой, если y_св(nT) с течением времени nT затухает, т.е

Из этого условия видно, что для затухания свободной составляющей неоюходимо и достаточно чтобы значения корней характеристического уравнения z_i по модулю были меньше 1.

Действительно, поскольку переменная z появилась в результате подстановки , то каждый корень z_i связан с корнями p_i в плоскости p зависимостью . Легко видеть, что нулевому корню, например p_i = 0, соответствует корень z₁ = 1. А корням p с отрицательными, вещественными частями соответствуют

Дадим условно устойчивости геометрический смысл. Для этого введем в рассмотрение плоскость z (рисунок 1). Тогда необходимое и достаточное условие устойчивости ИСАР формируется следующим образом:

Для устойчивости ИСАР необходимо и достаточно, чтобы все корни ее характеристического уравнения K(z) = 0 лежали внутри окружности единичного радиуса, построенной в начале координат комплексной плоскости z(z₁;z₂)/ Если хотя бы один корень лежит на этой окружности (корень z3), то система находится на границе устойчивости, при наличии корней на границе устойчивости. При наличии корней | z_i |>1 система неустойчива (z₄).

Рисунок 1

Определение корней при k>3 сопряжено с известными трудностями. поэтому на практике находят применение косвенные оценки – критерии устойчивости, которые позволяют оценивать устойчивость ИСАР без нахождения корней.

2) Аналог критерия устойчивости Рауса – Гурвица

Непосредственное применение этого критерия к характеристическому уравнению системы

недопустимо, так как выполнение условий Гурвица для этого уравнения свидетельствует о том, что все его корни лежат в левой полуплоскости плоскости , что не является необходимым и достаточным условием устойчивости ИСАР.

Для применения критерия используют, так называемое, билинейное преобразование.

Рассмотрим основное содержание этого преобразования. Для этого введем новый оператор , откуда (1)

Установим связь между плоскостями и . Для этого представим их так, как указано на рисунке 2.

Рисунок 2

Очевидно, что точке в плоскости соответствует в плоскости , также точке в плоскости соответствует точка в плоскости . Соответствие рассматриваемых точек показано стрелками.

Определим на плоскости линию отображающую окружность единичного радиуса в плоскости . Учитывая, что , где – оператор Лапласа, переменная будет иметь вид:

, где – модуль комплексной переменной на окружности единичного радиуса , откуда . Тогда для корней, лежащих на окружности .

Учитывая уравнение (1), уравнение искомой линии будет иметь вид .

Умножая числитель и знаменатель этого выражения на произведение и используя формулу Эйлера, будем иметь

.

Если учесть, что , то , (2)

где – относительная псевдочастота. При изменении ω от 0 до , вектор движется по верхней полуокружности, а величина изменяется от 0 до +∞, то есть верхней единичной полуокружности в плоскости соответствует положительная мнимая полуось в плоскости .

Аналогично, можно показать, что нижняя полуокружность в плоскости отобразится в отрицательную мнимую полуось в плоскости . Для этого необходимо частоту ω изменять в пределах от 0 до .

Таким образом, установлено, что линии единичной окружности в плоскости соответствует мнимая ось в плоскости . При этом значения переменной на этой оси определяются равенством (2).

Очевидно, что внутренняя область единичного круга в плоскости отображается в левую, а внешняя – в правую полуплоскость области . Исходя из этого, условие устойчивости ИСАР можно сформулировать следующим образом:

Для устойчивости ИСАР необходимо и достаточно, чтобы все корни ее характеристического уравнения, записанного относительно переменной ,

лежали в левой полуплоскости комплексной плоскости корней .

Оценим устойчивость системы, рассмотренной в примере § 5. Ее передаточная функция в разомкнутом состоянии , откуда – система находится на границе устойчивости.

Характеристическое уравнение замкнутой системы . Выполняя над ним билинейное преобразование будем иметь .

Отсюда получаем два условия устойчивости: kT > 0 и kT < 2.

Второе условие раскрывает важное свойство ИСАР: их устойчивость зависит не только от общего коэффициента передачи k разомкнутой системы, как это имеет и в непрерывных системах, но и от периода дискретности T: чем больше T, тем труднее обеспечить устойчивость системы при неизменном k.

Если , то

.

Исследование устойчивости систем 3-го и более высоких порядков проводят с помощью определителей Гурвица.

3) Аналог критерия устойчивости Михайлова

Рассмотрим характеристический полином замкнутой системы степени k и представим его в виде произведения сомножителей

где – корни уравнения.

Рассмотрим текущий вектор , модуль которого равен 1, тогда характеристический вектор замкнутой системы будет иметь вид

Определим угол поворота каждого вектора-разности стоящего в скобках. На рисунке 3 показаны векторы соответствующие корням и .

Рисунок 3

При изменении ωT от 0 до 2π конец вектора и концы векторов-разностей движутся по окружности единичного радиуса. При этом:

; .

Если характеристическое уравнение системы имеет l корней с , а следовательно – корней с , то результирующее изменение аргумента характеристического вектора

.

В устойчивой системе все , а следовательно . В этом случае

.

В силу симметрии комплексной плоскости относительно вещественной оси, изменение угла ωT можно ограничить пределами от 0 до π, что соответствует изменению частоты в пределах от 0 до или . В этом случае математическая запись критерия Михайлова будет иметь вид

.

Таким образом, для устойчивости ИСАР необходимо и достаточно, чтобы годограф Михайлова обходил последовательно 2k квадрантов комплексной плоскости против часовой стрелки, при изменении ωT от 0 до π, где k – степень характеристического полинома.

Оценим устойчивость замкнутой системы, рассматриваемой в качестве примера. Ее характеристическое уравнение , подставляя в него получим

.

Изменяя ωT от 0 до π , строим кривую Михайлова. Анализ кривой показывает, что система устойчива.

На рисунке 4 приведены годографы устойчивых систем 2-го и 3-го порядков.

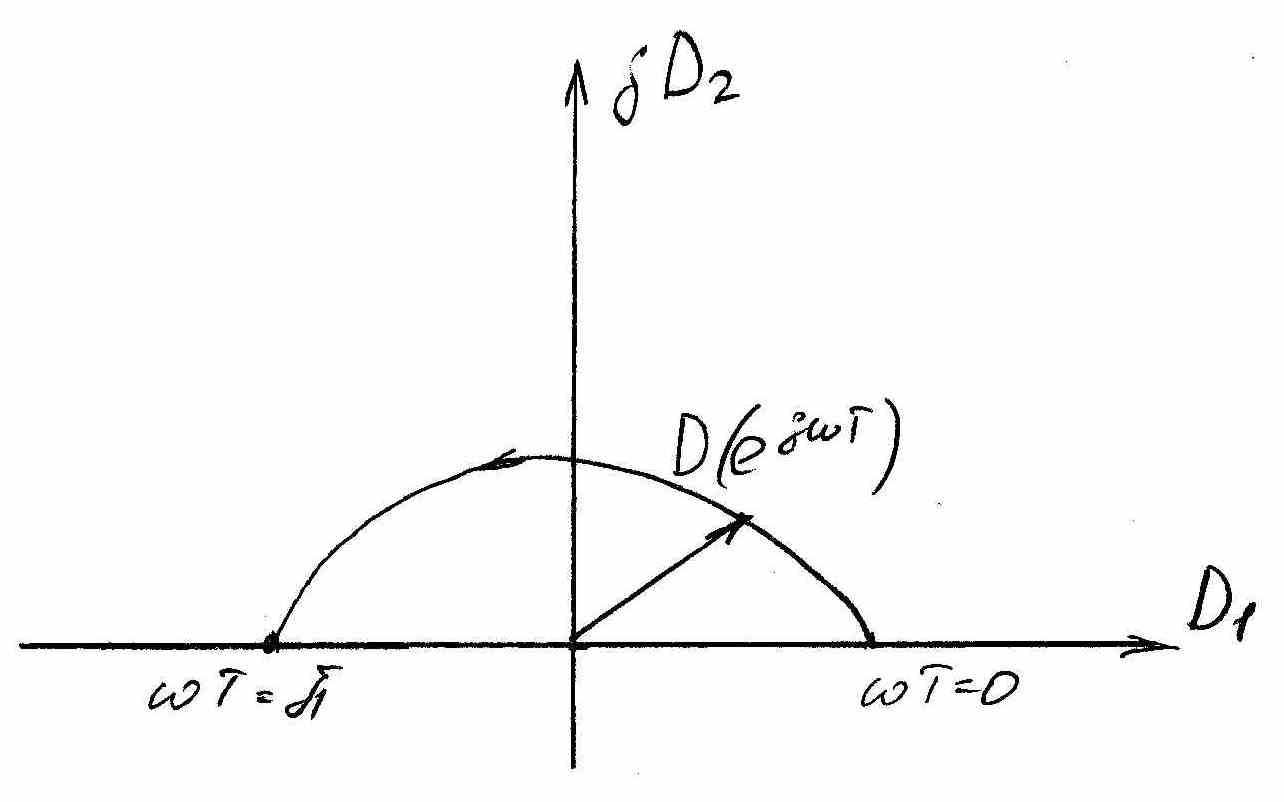
Рисунок 4

4) Аналог критерия устойчивости Найквиста

Пусть передаточная функция разомкнутой САР

Образуем вспомогательную функцию

где – характеристический полином замкнутой системы. Выполняя подстановку получим .

Рассмотрим случай, когда ИСАР в разомкнутом состоянии: устойчива, неустойчива и нейтрально устойчива.

1.ИСАР в разомкнутом состоянии устойчива.

Согласно критерию Михайлова

Для устойчивости замкнутой системы необходимо:

В этом случае

Т.о. замкнутая САР будет устойчива, если изменение вектора при равно 0 (рис.5)

Рисунок 5

Т.о. замкнутая САР будет устойчива, если АФХ разомкнутой устойчивой системы не охватывает точку (-1; j0) при изменении от 0 до

2. ИСАР в разомкнутом состоянии неустойчива.

В этом случае характеристическое уравнение разомкнутой системы имеет корней с . Тогда

Чтобы САР в замкнутом состоянии была устойчива необходимо

При этом

Т.о. замкнутая САР будет устойчива, если изменение вектора при изменении от 0 до равно

Рисунок

Иначе можно сказать, что для устойчивости замкнутой САР АФХ разомкнутой системы должна охватывать точку (-1; j0) раз в положительном направлении.

Следует отметить, что изменение аргумента вектора при движении его конца по замкнутому контуру равно 0 только тогда, когда начало вектора лежит вне контура. Устойчивость или неустойчивость разомкнутой САР определяется полностью непрерывной частью, т.к. полюса ПФ-и импульсной разомкнутой системы W(z) совпадают (с точностью до их мнимой части) с полюсами ПФ-и ее приведенной непрерывной части ПНЧ.

3.ИСАР в разомкнутом состоянии нейтрально устойчива.

В этом случае ее характеристическое уравнение имеет корни а следовательно оно может быть записано:

, где

- порядок астатизма, определяемый количеством корней .

Тогда ПФ-я разомкнутой системы:

Например при

В полученное выражение введем следующее обозначение или где . Отсюда следует, что точка на плоскости z охватывается дугой бесконечно малого радиуса , т.е. условно эту точку относят к внутренней области единичного круга. В этом случае .

Рисунок

Тогда при отображении дуги на плоскости W имеем дугу Г бесконечно большого радиуса R, изменяющегося от 0 до . Тогда не охватывает точку (-1; j0), а ПФ-я не имеет полюсов вне окружности единичного радиуса, что указывает на устойчивость ИСАР в замкнутом состоянии.

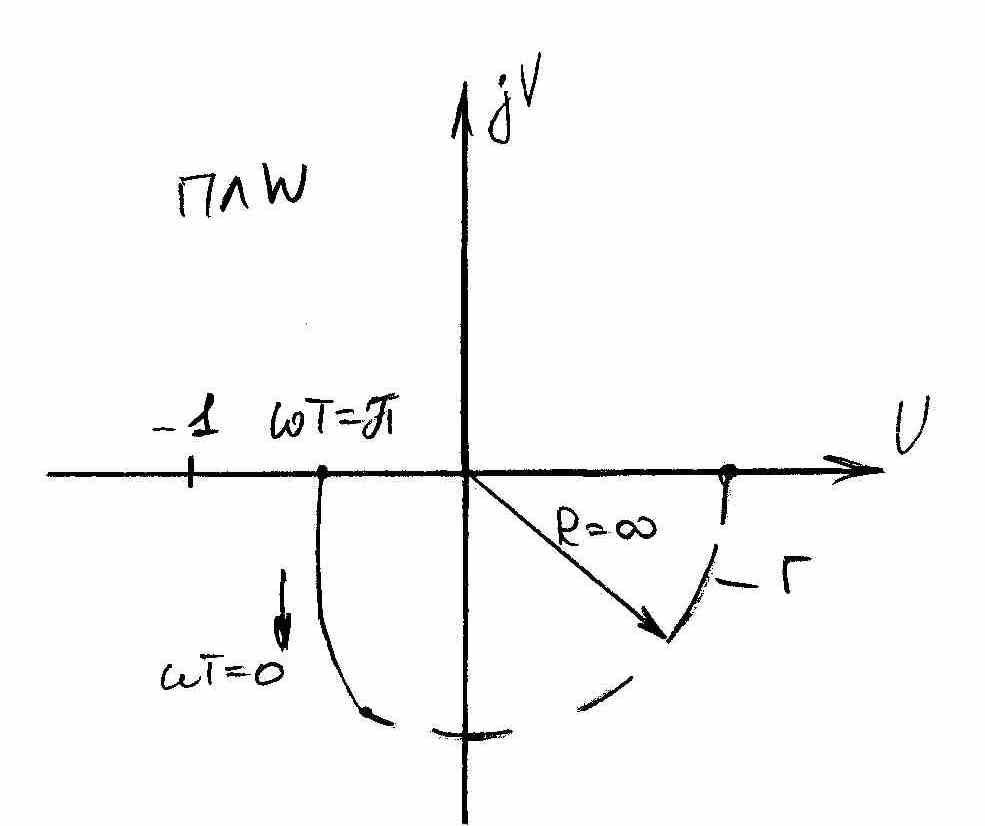
Рисунок