2.1.4. Естественный способ задания движения

Естественный способ задания движения точки применяется в случае, когда известна траектория точки (кривая или прямая). Рассматривая траекторию как криволинейную координатную ось, выберем на этой траектории неподвижную точку О и установим на ней «+» и «­­­­­­-» направления, как на обычной координатной оси (рис. 2.5). Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой S, равной расстоянию от точки О до точки М, измеренному вдоль дуги траектории, взятую с соответствующим знаком.

П ри движении точки м расстояние с течением времени изменяется. Чтобы знать положение точки м на траектории в любой

Рис. 2.5 момент времени надо знать криволинейную координату S в любой момент времени, то есть функцию изменения координаты S по времени:

. (2.4)

Уравнение (2.4) выражает закон движения точки м вдоль траектории.

Таким образом, чтобы задать движение точки естественным способом, нужно знать:

1. траекторию точки,

2. начало отсчёта О с указанием «+» и «­­­­­­-» направления отсчёта,

3. закон движения точки вдоль траектории в виде функции , где 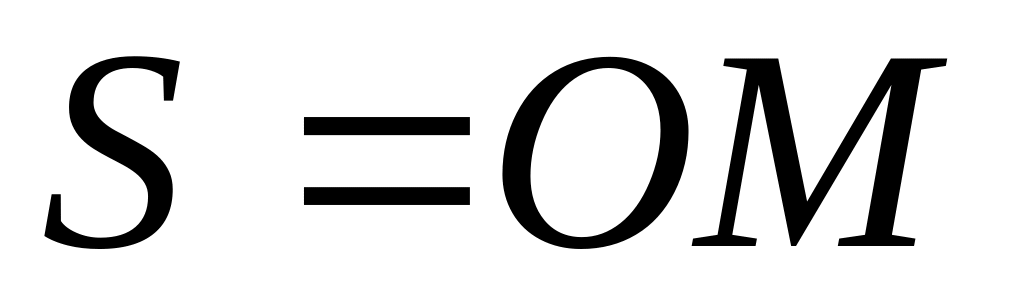(расстояние) определяет координату точки.

Дуговую координату не надо путать с длиной пути σ, пройденной движущейся точкой. Дуговая координата s точки М в некоторый момент времени t может равняться пути σ, пройденному за промежуток времени [0,t], только в том случае, когда движение началось из точки О и совершается в положительном направлении.

Путь, пройденный точкой за некоторый промежуток времени [0,t], определяется как предел суммы элементарных перемещений точки за этот промежуток времени:

, (2.5)

где – элементарное перемещение.

2. 2. Скорость точки

Скорость точки - это величина, характеризующая быстроту и направление движения точки в пространстве. Скорость - величина векторная.

2.2.1. Скорость точки при векторном способе задания движения.

Пусть в момент времени t точка занимает положение М, определяемое радиус-вектором , а в момент t₁= t + Δt – положение М₁, определяемое радиус-вектором ₁ (рис. 2.6). Из треугольника ОММ₁ имеем:

При перемещении точки ее радиус-вектор получает приращение .

Из этих выражений следует, что вектор перемещения точки является приращением радиус-вектора за промежуток времени Δt.

Отношение вектора перемещения точки к соответствующему промежутку времени определяет вектор средней по модулю и направлению скорости точки за этот промежуток времени Δt.

. (2.6)

Модуль средней скорости равен . Направлен

вектор так же, как , т.е. вдоль хорды ММ₁

Рис. 2.6 в сторону движения точки (от деления на Δt направление скорости не изменится).

Скоростью точки в данный момент времени t называется векторная величина , к которой стремится средняя скорость при стремлении промежутка Δt к нулю.

,

где Δt – приращение скалярного аргумента, а – приращение вектора функции .

Следовательно, предел отношения к Δt при Δt→0, является векторной производной по t.

,

тогда

. (2.7)

Вектор скорости точки в данный момент равен производной от радиус-вектора точки по времени.

Когда Δt → 0, а точка М₁ стремится к точке M, то предельным положением секущей ММ₁ является касательная в точке М. Откуда следует, что вектор скорости точки направлен по касательной к траектории в сторону движения точки.

При движении точки по криволинейной траектории величина и направление вектора скорости непрерывно изменяется (рис. 2.7). Выберем в пространстве некоторую неподвижную точку О₁, отложим от этой точки векторы, геометрически равные скоростям , , , (рис. 2.7).

Е сли от точки О₁ отложить скорости, соответствующие всем положениям точки М на кривой АВ, и соединить концы этих векторов, то получится линия СД, являющаяся годографом скорости. Другими словами, годограф

Рис. 2.7 скорости представляет собой геометрическое место концов векторов скорости движущейся точки, отложенных от одной и той же произвольной точки пространства (рис.2.7).

2.2.2. Скорость точки при координатном способе задания движения

Обозначим орты осей прямоугольной (Декартовой) системы координат - . Проведём из начала координат в точку М радиус-вектор (рис. 2.8). Так как проекции радиус-вектора равны: ; ; , то по (2.2)

.

Учитывая, что орты имеют неизменные величины и направления, возьмём производную от радиус-вектора .

С другой стороны, построив в точке М оси координат и проектируя на оси координат, (рис. 2.8) имеем:

.

Сравнивая эти два равенства, видим, что:

; ; , (2.8)

т о есть проекции скорости на оси координат равны первым производным от соответствующих координат точки во времени. Уравнения (2.8) являются параметрическими

Рис. 2.8 уравнениями годографа скорости.

Для нахождения годографа скорости в явном виде необходимо из уравнений (2.8) исключить параметр t.

По проекциям (2.8) находим модуль вектора

скорости

, (2.9)

и направление по его направляющим косинусов

; ; , (2.10)

где α, β, γ – углы между вектором скорости и осями координат.