5. Законы Ньютона

В основе классической механики лежат законы Ньютона (от­части известные из курса элементарной физики) и система аксиом, представляющих собой определенные знания, накопленные чело­вечеством в области механики.

Законы классической механики определяют наиболее общие I свойства механического движения. Аксиомы отличаются от законов ограниченностью своего содержания. Впрочем, деление основных положений механики на «законы» и «аксиомы» условно.

Здесь мы рассмотрим лишь основные законы классической ме­ханики. Систему аксиом изучим далее в первой части курса. При изложении законов Ньютона будем предполагать, согласно ска­занному выше, существование абсолютно неподвижной координат­ной системы.

Для технических расчетов можно всегда принять, что такой системой является гелиоцентрическая система координат. Однако в большинстве случаев можно допустить, что такой системой являет­ся даже система координат, связанная с Землей. (Более подробно это рассматривается в динамике относительного движения).

Все законы механики формулируются применительно к движе­нию материальной точки.

Предварительно ознакомимся лишь с законами, составляющими фундамент классической механики.

Первый закон Ньютона

Изолированная материальная точка сохраняет состояние рав­номерного и прямолинейного движения или находится в состоянии покоя.

Под изолированной материальной точкой следует понимать частицу вещества, находящуюся вне воздействий внешнего по отношению к ней мира, или находящуюся в таких условиях, что этими воздействиями можно пренебречь.

Первый закон Ньютона иначе называется законом инерции. Этим законом устанавливается основное свойство реальных тел природы сохранять свое состояние движения, если оно двигалось, и покоя, если находилось в состоянии покоя. Здесь Ньютон, следуя Галилею, отверг воззрение Аристотеля о том, что естест­венным состоянием вещества является состояние покоя.

Свойство изолированной материальной точки сохранять состо­яние равномерного и прямолинейного движения называется свой­ством инертности. Это свойство будем рассматривать как основ­ное свойство вещества наряду с теми простейшими свойствами, о которых речь шла ранее.

Еще Галилей заметил, что все тела, находя­щиеся в некоторой небольшой области вблизи земной поверхности, падают в пустоте с одинаковым ускорением g. Это ускорение на уровне моря и при 50° широты приближенно равно 9,81 м/сек². При изменении положения тел относительно земной поверхности ускорение g изменяется. Изменяется при этом и вес тела Р. Однако отношение Р/g не зависит от положения тела относительно земной поверхности. Это показывает, что отношение Р/g характеризует внутренние свойства вещества тела, а именно его гравитацион­ные свойства. Поэтому можно принять, что масса m материальной точки количественно определяется так:

Ряд опытов и наблюдений над взаимодействиями движущихся тел показал, что масса движущейся материальной точки характеризует то основное свойство вещества тел, кото­рое называется инертностью.

Второй закон Ньютона

Равнодействующая двух сил и определяется пo величине и направ­лению диагональю параллелог-рамма, построенного на отрезках, изображающих силы.

У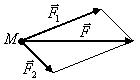 казанное правило сложения двух сил следует рассматривать как аксиому. Эта аксиома называется аксиомой о параллелограм­ме сил. Как известно из аналитической геометрии, правило парал­лелограмма есть частный случай правила сложения векторов — правила многоугольника векторов.

Это правило распространяется на любое количество сил и приводит к правилу многоугольника сил.

Второй закон Ньютона. Первая производная от количества движения по времени равна равнодействующей сил, действующих на точку. Его можно записать следующим равен­ством

, (в.1)

где — равнодействующая сил, действующих на материальную точку.

Если масса m точки не зависит от времени t, то равенство (в.1) можно представить так:

(в.2)

т. е. произведение массы точки на ее ускорение равно вектору равнодействующей сил, приложенных к точке.

Эта упрощенная формулировка второго закона Ньютона не­применима в механике точки переменной массы и в теории от­носительности.

Второй закон Ньютона устанавливает единство количествен­ного определения сил, приложенных к покоящимся и движущимся телам. Закон установлен на основании многочисленных наблюде­ний и опытов и является объективным законом природы, связы­вающим массу, ускорение точки и силу, к ней приложенную. Все эти величины определяются независимыми измерениями. Поэтому нельзя рассматривать второй закон Ньютона как «опре­деление массы» или «определение силы».

Со вторым законом Ньютона и аксиомой о параллелограмме сил связан закон независимости действия сил. Этот закон, уста­новленный в XVIII—XIX веках, также причисляется к законам классической механики.

Закон независимости действия сил заключается в следующем. Если материальная точка находится под действием системы сил, то каждая сила сообщает точке ускорение, согласно второму за­кону Ньютона, независимо от действия остальных сил.

Третий закон Ньютона

Третий закон Ньютона носит название закона ра­венства действия и противодействия.

Если некоторое тело действует на материальную точку с силой , то материальная точка действует на это тело с силой , равной по величине и прямо противоположной по направлению силе . Линии действия сил и совпадают.

Сила называется действием, а сила —противодействием. Таким образом, третий закон Ньютона можно кратко сформу­лировать так: действие равно и прямо противоположно по на­правлению противодействию.

Применение законов Ньютона и развитие следствий, вытекающих из этих законов, составляют основную часть содержания курса теоретической механики. Теоретическая механики делится на: кинематику, и кинетику, состоящую из геометрической статики и динамики.

В геометрической статике рассматриваются свойства сил, по­зволяющие, в частности, заменять некоторую систему сил, дей­ствующих на материальную точку или на абсолютно твердое тело, другой системой сил, производящей то же самое механи­ческое действие, которое производит первая система сил. Такие системы сил называются эквивалентными.

Кинематика изучает геометрические свойства механических движений, не рассматривая физических факторов, с которыми связаны эти геометрические свойства, т. е. независимо от дей­ствия сил. Поэтому кинематику можно назвать «геометрией движения».

Наконец, динамика изучает наиболее общие свойства механи­ческих движений, а именно те свойства, в которых выявляется внутренняя связь геометрических свойств механических движений и свойств сил, отклоняющих движение точек системы от равно­мерного и прямолинейного движения.

Раздел первый КИНЕМАТИКА

--------------------------------------------------------------------------