3.2.4. Динаміка відносного руху точки

Основне рівняння динаміки точки (3.3) виконується в умовно нерухомій системі координат.

Мета подальшого викладу – встановити закон, за яким можна складати диференціальне рівняння руху точки в рухомій системі координат, тобто встановити, що відповідає другому закону І.Ньютона в рухомій системі координат.

Нехай відносно рухомого тіла, з яким жорстко з’єднана рухома система координат , рухається точка М.

Рух тіла відбувається відносно нерухомої системи координат (рис. 3.13). Визначимо рух точки М відносно системи .

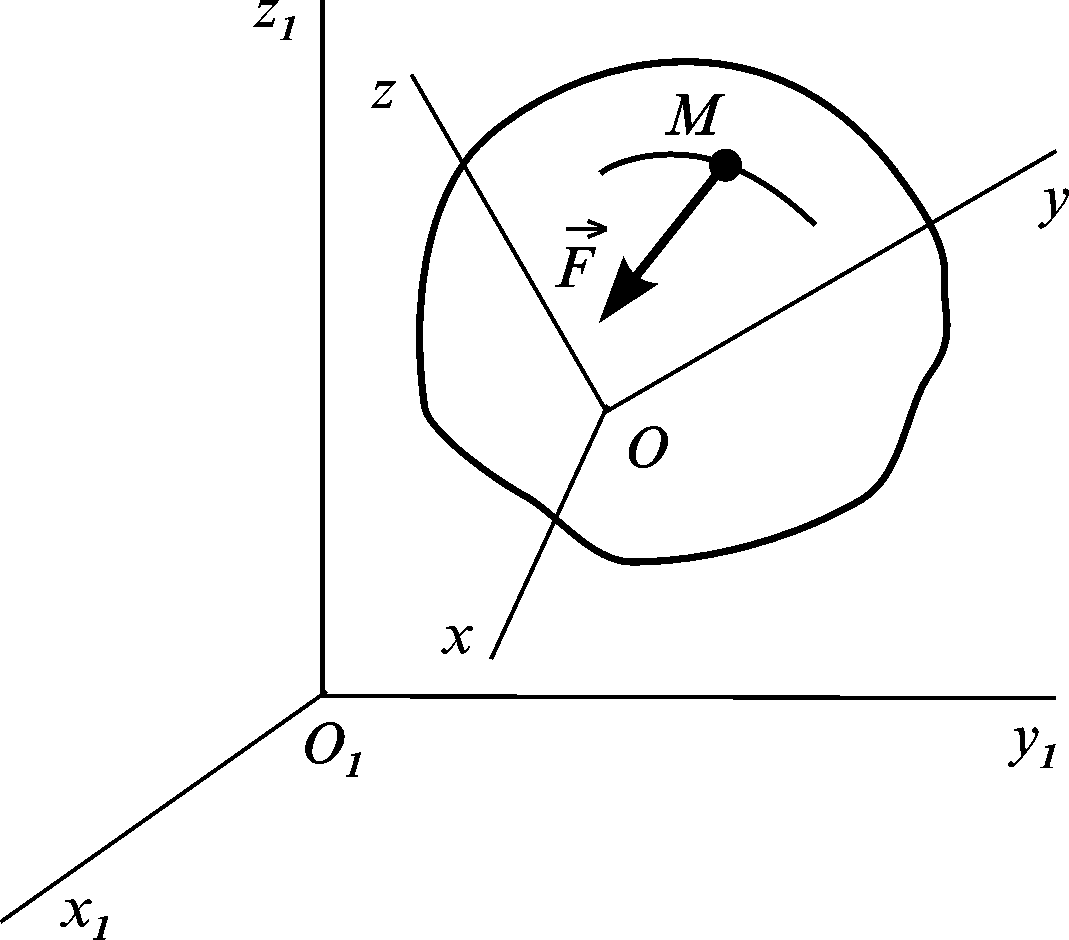
Рисунок 3.13

Другий закон І.Ньютона справджується в абсолютному русі, тобто

. (3.80)

На підставі теореми Коріоліса

.

Тоді (3.80) набуде вигляду

,

звідки

. (3.81)

Оскільки згідно з (3.69)

— переносна сила інерції;

— коріолісова сила інерції,

то (3.81) набуде вигляду

. (3.82)

Це рівняння є основним законом динаміки у відносному русі:

добуток маси на відносне прискорення точки дорівнює векторній сумі рівнодійної сил, прикладених до точки, сили інерції переносного руху і коріолісової сили інерції.

Таким чином, прикладаючи до точки сили інерції переносного руху і коріолісову силу інерції, ми ніби зупиняємо рухому систему.

Щоб з’ясувати фізичний зміст цих сил інерції, розглянемо приклад, у якому рухомим тілом є земна куля (рис. 3.14), що обертається навколо власної осі (рух Землі навколо Сонця не розглядаємо). Нехай уздовж меридіана з півночі на південь рухається точка (вагон по рейках, частинка води у річці тощо).

Як відомо, коріолісове прискорення точки напрямлене із заходу на схід, а відповідна сила інерції за третім законом Ньютона прикладена до Землі і діє зі сходу на захід, внаслідок чого частинки води в північній півкулі розмивають правий берег (ефект Бера), праві рейки спрацьовуються швидше, ніж ліві тощо.

Таким чином,

якщо між точкою й тілом, рух якого є переносним, існує фізичний зв’язок, то сили інерції цілком реальні, але прикладені до тіла, яке здійснює переносний рух.

Рівняння (3.82) дає змогу також описувати рух точки відносно будь-якої рухомої системи координат, навіть не зв’язаної з точкою, наприклад, рух маятника Фуко відносно тролейбуса, який рухається вулицею. У таких випадках сили інерції є часто уявними математичними додатками, які вво- дяться до рівняння зовсім абстрактно.

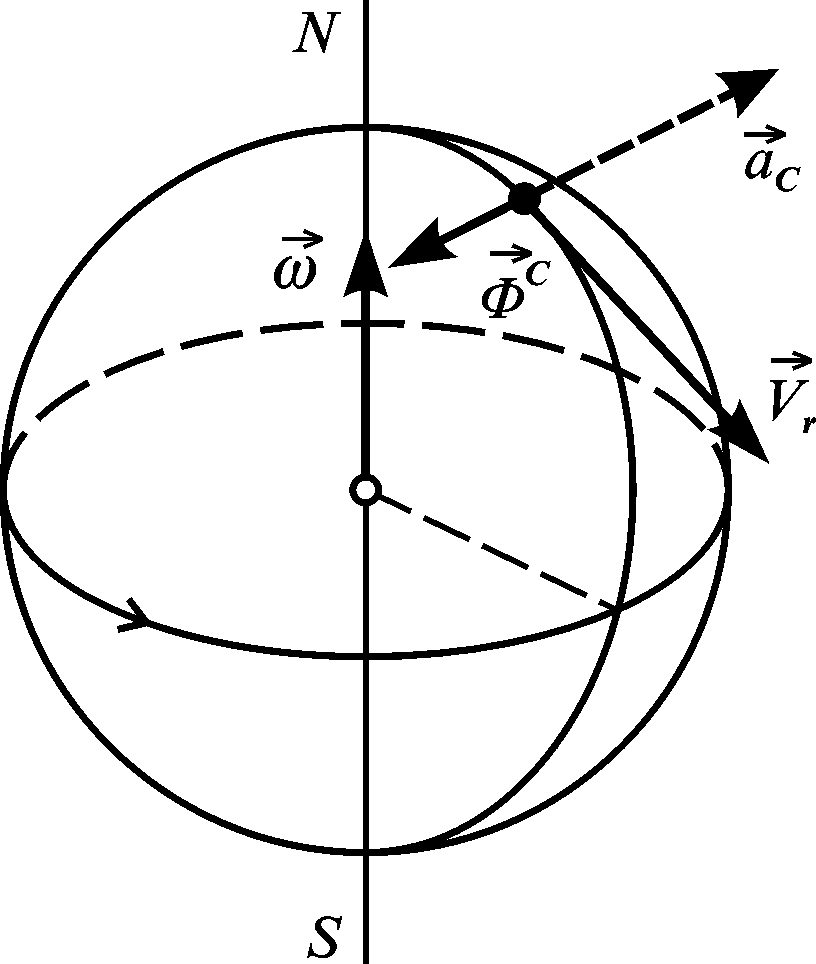
Рисунок 3.14

Вони є математичними поправками на неінерціальність системи координат.

Системи координат, у яких виконуються закони І.Ньютона, називають інерціальними.

Ця назва, очевидно, пов’язана з першим законом І.Ньютона – законом інерції. За І.Ньютоном, нерухомою системою координат є геліоцентрична. Але вона також рухома, оскільки Сонце і зірки рухаються. Відомо, що всі розрахунки на підставі законів класичної механіки мають досить велику точність. Це свідчить про те, що поправка на неінерціальність, яка дорівнює сумі , досить мала як у геліоцентричній, так і в геоцентричній системах координат.

Розглянемо поняття відносної рівноваги точки.

Точка знаходиться у стані відносної рівноваги, якщо протягом скінченного проміжку часу її відносна швидкість і відносне прискорення дорівнюють нулеві, тобто . На підставі цього означення та рівняння (3.82) дістанемо необхідну умову відносної рівноваги

. (3.83)

З’ясуємо, враховуючи (3.83), чим відрізняється одна від одної сили тяжіння і ваги.

З

Рисунок 3.15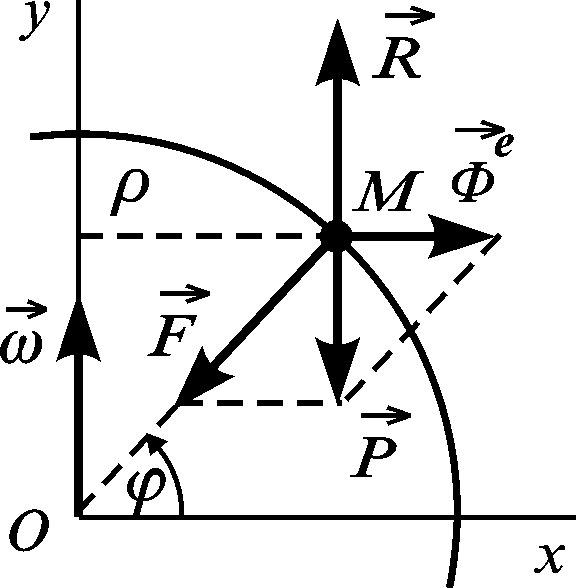

важувати маємо певну точку М на пружинних терезах поблизу поверхні Землі (рис. 3.15). На точку діє сила Всесвітнього тяжіння , яка напрямлена до центра Землі О, пружна сила з боку “в’язі” – пружини, а оскільки точка знаходиться у стані відносної рівноваги, то ще й сила – сила інерції переносного руху (за рахунок обертання Землі навколо власної осі).

Векторна сума цих сил дорівнює нулеві:

. (3.84)

Пружна сила (покази терезів) дорівнює за модулем силі ваги , тобто

. (3.85)

Отже, сила ваги дорівнює векторній сумі сили тяжіння та переносної сили інерції.

Довгий час силу не враховували, не помічаючи її через те, що вона дуже мала. Дійсно, модуль

,

де – радіус паралелі, яка проходить через точку; ; – кутова швидкість обертання Землі

рад/с 72,710^-6 рад/с,

тобто є дуже малою величиною.

Нарешті, з’ясуємо, які кінематичні ознаки інерціальних систем координат. Для цього треба, щоб додаток в (3.82) у вигляді суми дорівнював нулеві.

Модуль коріолісової сили інерції

.

Достатньою умовою рівності її нулеві є , тобто тіло повинно рухатися поступально.

Сила інерції переносного руху складається з дотичної і нормальної сил:

.

Перша складова дорівнює нулеві, якщо тіло рухається рівномірно , а друга – – якщо прямолінійно .

Отже,

інерціальна система координат – це така, що рухається поступально, рівномірно і прямолінійно.

Якщо існує хоча б одна інерціальна система координат, то будь-яка інша система координат, яка рухається відносно першої поступально, прямолінійно і рівномірно, також інерціальна. У механіці це твердження називають принципом відносності Галілея.

Приклад 3.3. Точка М масою ковзає вздовж гладенького півкола АМВ (рис. 3.16) пластини АBCD, яка рухається вздовж осі зі сталим прискоренням .

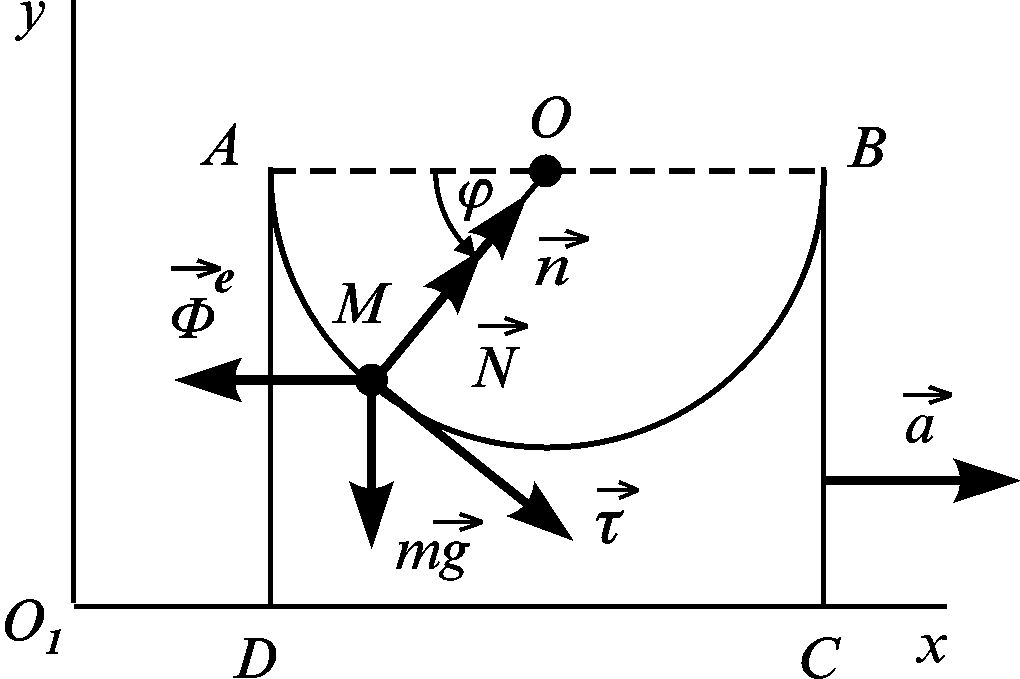
Рисунок 3.16

Знайти тиск на пластину точки М у найнижчому положенні, якщо в положенні А відносна швидкість точки М дорівнювала нулеві.

Розглянемо рух точки М відносно кривої АВ. До точки прикладено силу ваги і реакцію півкола, яка перпендикулярна до нього. Тіло, відносно якого визначатиметься рух точки М, рухається з прискоренням прямолінійно і поступально, тому до точки потрібно прикласти тільки одну силу інерції переносного руху, яка дорівнює і напрямлена вліво.

Складаємо диференціальні рівняння відносного руху точки М у натуральній формі:

(3.86)

Відомо, що

Отже,

(3.87)

Реакцію , яка дорівнює тискові визначатимемо з другого рівняння, але для цього потрібно знайти .

Зауважимо, що .

Підставимо цей вираз у перше рівняння системи (3.87)

.

Тепер розділимо змінні

і проінтегруємо цей вираз

. (3.88)

Сталу знаходимо на підставі початкової умови з рівняння (3.88):

.

Отже, вираз (3.88) остаточно має вигляд

.

Цей вираз підставляємо в друге рівняння системи (3.87) і знаходимо

.

Таке значення має нормальна реакція у довільному положенні точки М. У найнижчому положенні . Отже,

.

За третім законом І.Ньютона тиск точки на криву дорівнює за модулем силі , але напрямлений у протилежний бік.