Тренд в форме кривой Гомперца
Признак обнаружения тренда:
Вычисляются величины:
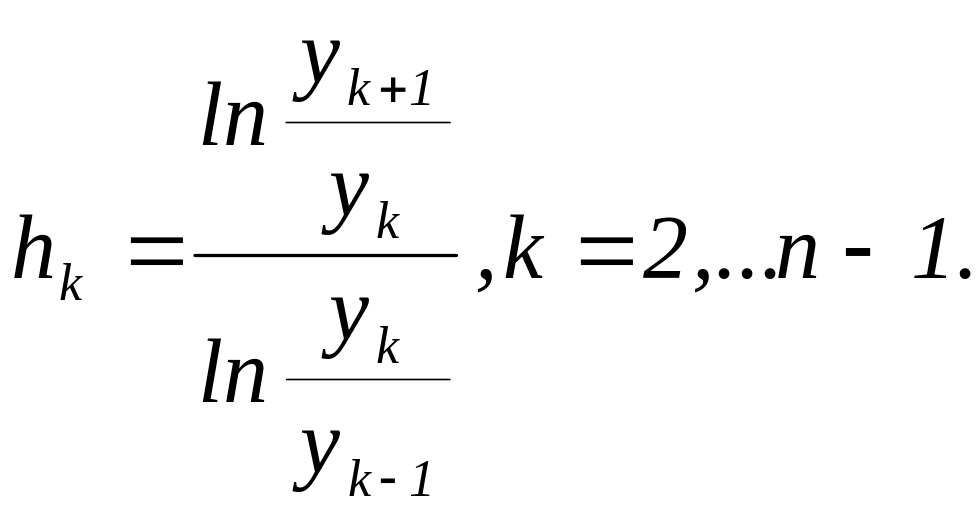
В полученном ряду hk проверяется гипотеза о наличии тренда методом Фостера-Стюарта. Вычисления приведены в предыдущей таблице.
Получаем d=-3; σ2=1,82, n=41, получим τd=-1,65.
По таблице Стьюдента для уровня значимости 5 % находим =2,210.
Так как (1,65 < 2,210), то тренд в форме кривой Гомперца возможен.
Таким образом, возможные модели тренда таковы: модифицированный экспоненциальный, кубический, логистический и в форме кривой Гомперца.
4. Нахождение коэффициентов и сравнение трендовых моделей Модифицированный экспоненциальный тренд
Для
нахождения коэффициентов тренда в виде
модифицированной экспоненты
воспользуемся формулами Брианта:
,
,
.
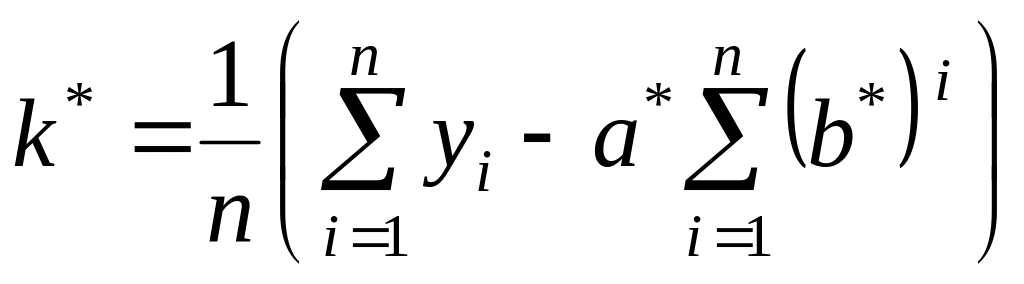Вычисления приведены в таблице.
i |
yi |
yi * yi+1 |
yi^2 |
b^i |
b^2i |
b^i * yi |
U(i) |
(yi-U(i))^2 |
1 |
753,664 |
584694,0385 |
568009,4249 |
0,63 |
0,3969 |
474,8083 |
747,3006 |
40,49286 |
2 |
775,802 |
612492,5758 |
601868,7432 |
0,3969 |
0,15753 |
307,9158 |
773,2633 |
6,445109 |
3 |
789,496 |
620885,7078 |
623303,934 |
0,250047 |
0,062524 |
197,4111 |
789,6198 |
0,015318 |
4 |
786,433 |
618537,4188 |
618476,8635 |
0,15753 |
0,024816 |
123,8865 |
799,9244 |
182,0166 |
5 |
786,510 |
628540,253 |
618597,9801 |
0,099244 |
0,009849 |
78,05613 |
806,4162 |
396,2585 |
6 |
799,151 |
647455,358 |
638642,3208 |
0,062524 |
0,003909 |
49,96572 |
810,5061 |
128,939 |
7 |
810,179 |
662785,5651 |
656390,012 |
0,03939 |
0,001552 |
31,91279 |
813,0828 |
8,431842 |
8 |
818,073 |
667360,2293 |
669243,4333 |
0,024816 |
0,000616 |
20,30095 |
814,706 |
11,33641 |
9 |
815,771 |
656325,295 |
665482,3244 |
0,015634 |
0,000244 |
12,75361 |
815,7287 |
0,001789 |
10 |
804,546 |
650109,3726 |
647294,2661 |
0,009849 |
9,7E-05 |
7,924217 |
816,373 |
139,8776 |
11 |
808,045 |
664261,4727 |
652936,722 |
0,006205 |
3,85E-05 |
5,013968 |
816,7789 |
76,28067 |
12 |
822,060 |
677326,0613 |
675782,6436 |
0,003909 |
1,53E-05 |
3,213587 |
817,0346 |
25,2547 |
13 |
823,938 |
672824,0668 |
678873,0039 |
0,002463 |
6,07E-06 |
2,029184 |
817,1957 |
45,45194 |
14 |
816,596 |
660659,6444 |
666829,0272 |
0,001552 |
2,41E-06 |
1,266995 |
817,2972 |
0,491664 |
15 |
809,041 |
652337,0397 |
654547,3397 |
0,000977 |
9,55E-07 |
0,790822 |
817,3611 |
69,22453 |
16 |
806,309 |
661777,3054 |
650134,2035 |
0,000616 |
3,79E-07 |
0,496535 |
817,4014 |
123,0416 |
17 |
820,749 |
681059,1617 |
673628,921 |
0,000388 |
1,51E-07 |
0,31842 |
817,4268 |
11,03709 |
18 |
829,802 |
678488,4351 |
688571,3592 |
0,000244 |
5,97E-08 |
0,202817 |
817,4428 |
152,7504 |
19 |
817,651 |
659541,0085 |
668553,1578 |
0,000154 |
2,37E-08 |
0,125904 |
817,4528 |
0,039264 |
20 |
806,629 |
654685,1019 |
650650,3436 |
9,7E-05 |
9,41E-09 |
0,07825 |
817,4592 |
117,2931 |
21 |
811,631 |
665048,0065 |
658744,8802 |
6,11E-05 |
3,74E-09 |
0,049603 |
817,4632 |
34,01447 |
22 |
819,397 |
683055,8944 |
671411,4436 |
3,85E-05 |
1,48E-09 |
0,031549 |
817,4657 |
3,729875 |
23 |
833,608 |
686432,0068 |
694902,2977 |
2,43E-05 |
5,88E-10 |
0,020221 |
817,4673 |
260,5223 |
24 |
823,447 |
673244,5031 |
678064,9618 |
1,53E-05 |
2,34E-10 |
0,012584 |
817,4683 |
35,74488 |
25 |
817,593 |
662865,9775 |
668458,3136 |
9,63E-06 |
9,27E-11 |
0,007871 |
817,4689 |
0,015394 |
26 |
810,753 |
668654,7539 |
657320,427 |
6,07E-06 |
3,68E-11 |
0,004917 |
817,4693 |
45,10901 |
27 |
824,733 |
682555,6287 |
680184,5213 |
3,82E-06 |
1,46E-11 |
0,003151 |
817,4696 |
52,75735 |
28 |
827,608 |
682836,1878 |
684935,0017 |
2,41E-06 |
5,8E-12 |
0,001992 |
817,4697 |
102,7845 |
29 |
825,072 |
671234,8504 |
680743,8052 |
1,52E-06 |
2,3E-12 |
0,001251 |
817,4698 |
57,79297 |
30 |
813,547 |
660041,2572 |
661858,7212 |
9,55E-07 |
9,13E-13 |
0,000777 |
817,4699 |
15,38909 |
31 |
811,313 |
667243,2827 |
658228,784 |
6,02E-07 |
3,62E-13 |
0,000488 |
817,4699 |
37,90782 |
32 |
822,424 |
682853,7127 |
676381,2358 |
3,79E-07 |
1,44E-13 |
0,000312 |
817,47 |
24,54253 |
33 |
830,294 |
683616,7528 |
689388,1264 |
2,39E-07 |
5,71E-14 |
0,000198 |
817,47 |
164,4557 |
34 |
823,343 |
668855,0362 |
677893,6956 |
1,51E-07 |
2,27E-14 |
0,000124 |
817,47 |
34,49233 |
35 |
812,365 |
656732,1133 |
659936,8932 |
9,48E-08 |
8,99E-15 |
7,7E-05 |
817,47 |
26,06092 |
36 |
808,420 |
667087,1651 |
653542,8964 |
5,97E-08 |
3,57E-15 |
4,83E-05 |
817,47 |
81,90238 |
37 |
825,174 |
683027,0512 |
680912,1303 |
3,76E-08 |
1,42E-15 |
3,11E-05 |
817,47 |
59,35168 |
38 |
827,737 |
680319,5235 |
685148,5412 |
2,37E-08 |
5,62E-16 |
1,96E-05 |
817,47 |
105,4113 |
39 |
821,903 |
672102,1373 |
675524,5414 |
1,49E-08 |
2,23E-16 |
1,23E-05 |
817,47 |
19,6515 |
40 |
817,739 |
662161,702 |
668697,0721 |
9,41E-09 |
8,86E-17 |
7,7E-06 |
817,47 |
0,072362 |
41 |
809,747 |
662823,2653 |
655690,204 |
5,93E-09 |
3,51E-17 |
4,8E-06 |
817,47 |
59,64472 |
42 |
818,556 |
680129,9948 |
670033,9251 |
3,74E-09 |
1,4E-17 |
3,06E-06 |
817,47 |
1,179397 |
43 |
830,890 |
682962,4989 |
690378,1921 |
2,35E-09 |
5,54E-18 |
1,96E-06 |
817,47 |
180,0964 |
44 |
821,965 |
663101,3586 |
675626,4612 |
1,48E-09 |
2,2E-18 |
1,22E-06 |
817,47 |
20,20503 |
45 |
806,727 |
|
|
9,34E-10 |
8,72E-19 |
7,53E-07 |
817,47 |
115,412 |
|
36596,431 |
29161129,77 |
29121823,1 |
1,702703 |
0,6581 |
1318,607 |
|
|
|
syi_n |
syi-yi+1 |
syi^2 |
sb^I |
sb^2i |
sb^i*yi |
|
3072,926 |
Получаем:
;
;
.
.
Сумма квадратов отклонений тренда от динамического ряда:
.
График найденного тренда с графиком динамического ряда представлен ниже.