14.4. Нормальна форма рівнянь у просторі станів

Нормальна форма рівнянь у просторі станіввиходить зі стандартної форми (14.1) за допомогою перетворення подоби. При цьому передбачається, що власні числа матриці А різні.

Уведемо лінійне перетворення

X=MQ, (14.28)

де М - модальна матриця матриці А.

Рівняння (14.1) перепишемо

(14.29)

Помноживши перше рівняння з (14.29) ліворуч на М^-1 , одержимо

(14.30)

Тому що M - модальна матриця, то

М^-1АМ =  = - діагональна матриця;

де _i (при i = 1, 2, ... , n) - власні числа матриці .

Отже, можна записати

(14.31)

де =М^-1АМ, В_n= М^-1B, C_n=CM, D_n=D  матриці;

Q=[q₁,q₂,...,q_n]^T - вектор стану системи, елементами якого є нові змінністану q_i (при i=1, 2, ... , n).

Система (14.31) являє собою нормальну форму рівнянь опису систем керування в просторі станів.

Нормальна форма рівнянь стану дозволяє декомпозировать багатозв’язану систему n-го порядку на n незв’язаних систем, при цьому диференціальні рівняння стають розв'язаними щодо зміннихстану q₁,q₂,...,q_n, тобто вони мають вигляд

(14.32)

де f_i - зовнішній вплив на i-ю зміннустану.

Таким чином, перехід до нормальної форми істотно спрощує дослідження багатозв’язаних систем.

У випадку кратних власних чисел матриці A діагональна матриця ( заміняється матрицею J, що будується із клітокЖордана, наприклад,

. (14.33)

Таким чином, зпорівняннярівнянь (14.1) і (14.31) випливае, щоприматематичномуописітогосамогодинамічногопроцесурізномувиборузміннихстанувідповідаютьрізніматрицісистеми, керування, спостереження, зв'язкийрізнівекторнідиференціальнірівняння, кожнезякихповністювизначаєвихіднувеличинусистеми.

Приклад.Написати рівняння станів у нормальній формі для динамічної системи, представленої на рис.14.3.

Рис. 14.3. Структурна схема системи в зміннихстану

Рішення. Виберемо в якості зміннихстану системи сигнали на виходах інтеграторів x1 і x2. У цьому випадку структурній схемі (рис.14.3) відповідає наступна система рівнянь ( стандартна форма)

Звідки матриці

, B= , C= , D=[2].

Власні числа матриці A: ₁= 1, ₂= 2.

Модальна матриця M= і M^-1= .

Тоді діагональна матриця системи, матриця керування, матриця спостереження й матриця зв'язку будуть

= , В_n= М^-1B= , C_n=CM=[-1 -1], D_n=D=[2].

Звідси одержуємо рівняння станів системи в нормальній формі

яким відповідає структурна схема системи, наведена на рис.14.4.

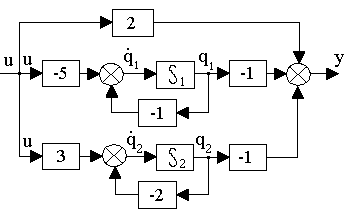
Рис. 14.4. Структурна схема системи в зміннихстану

по полюсах

14.5. Керування по стану. Системи керування

станом

Підключення додаткових контурів зворотногозв'язка в багатоконтурних системах забезпечує підвищення якості керування. Найбільш повна інформація про керований об'єкт утримується в зміннихстану. Керування по станупередбачаєвведення в структуру системи контурів прямих і зворотних зв'язків по зміннимстану об'єкта керування. При цьому завдання стабілізації й спостереження формулюється якзавдання підтримки постійного X* = const або змінюється по заданому закону X* (t) стану об'єкта керування X* = X* (t).

Що змінюются в часі або фіксовані сигнали x_i* , що визначають необхідний характер зміни зміннихстану x_i, становлять розширений вектор завдання X* =  x_i* , а помилка руху об'єкта керування по станівизначається вектором відхиленняe = X*  X.

Управління по стану, як і керування по виходу об'єкта керування, може бути розімкнутим: U = F[X*], замкнутимU = F[e], або комбінованим: U = F[e, X*].

Системи з регуляторами стануставляться до багатоконтурних систем і, отже, мають кращі точностні й динамічні властивості, чимодноконтурні. Вони проектуються для керування як одномірними, так і багатомірними об'єктами керування.

Проаналізуємо використання лінійних регуляторів стану для рішеннязавдань стабілізації й спостереження.

Розглянемозавдання стабілізації об'єкта керування (ОК) у крапці Y* = 0, думаючи, що при цьому вектор стану також приймає нульове значення: X* = 0 (до такого видузавдання майже завжди може бути наведена перетворенням координат векторів X і Y).

Найпростіший регулятор стану - пропорційний або модальний регулятор уводить зворотні зв'язки по всімзмінним x_i (рис. 14.5).

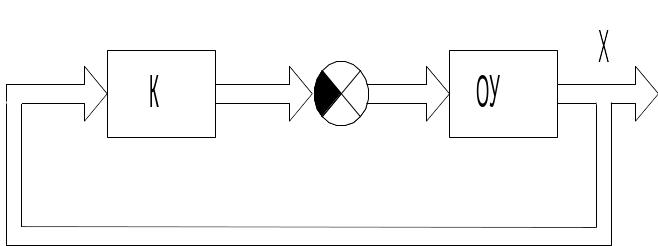
Рис. 14.5. Структурна схема системи зП-Регулятором

Модальний регулятор реалізує пропорційний закон керування

U = - KX , (14.34)

де K - матриця коефіцієнтів зворотногозв'язка по стану.

Для одномірного об'єкта керування як координати x_i вектора X можна вибрати, наприклад, фазові змінніy, , ..., y^{( n-1)} , тобто

X = [ x₁ x₂ ... x_n ]^T = [ y ... y^{( n-1)} ]^T , (14.35)

де ; n - порядок системи.

Тоді K = [ k₁k₂ ... k_n ]. Вираження (14.34) можна записати в скалярній формі

Перші члени закону керування (14.36) відповідають описуПД-регулятора виходу при y* = 0.

Таким чином, регулятори станує узагальненням ПД-регуляторів, хоча й не містять у явному виді ланок, що диференціюють. Вибір коефіцієнтів k матриці зворотногозв'язка K забезпечує одержання заданих динамічних властивостей системи.

В умовах дії на об'єкт керування зовнішніх збурювань F точностні показники якості системи із пропорційним регулятором стану обмежені. Зниження сталих помилок досягається введенням до складу регулятора контурів інтегральних зворотних зв'язків (рис. 14.6).

Рис. 14.6. Структурна схема системи з ПІ-регулятором

ПІ-регулятор реалізує пропорційно-інтегральний закон керування

(14.37)

де K_I - матриця зворотних зв'язків по інтегралу від вектора стану.

Комбінований регулятор дозволяє забезпечити компенсацію збурювання за рахунок прямих зв'язків по впливу, що обурює, F (рис. 14.7).

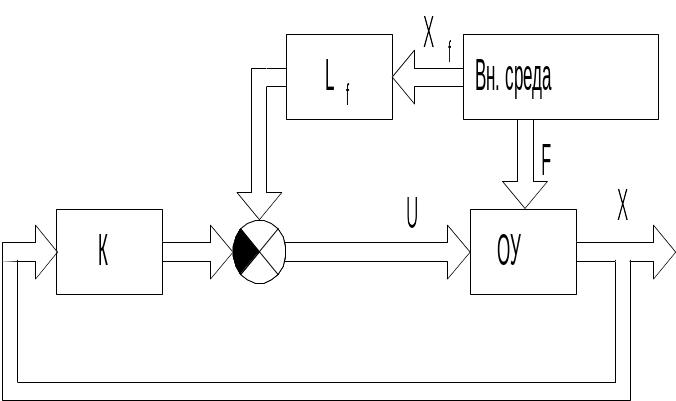
Рис. 14.7. Структурна схема комбінованої системи по впливу, що обурює

У цьому випадку закон керування приймає вид

U = KXL_FX_F , (14.38)

де L_F - матриця коефіцієнтів контуру зв'язків по F;

X_F - вектор, складений зі збурювання F і його похідних.

Завдання спостереження розглядається як завдання відпрацьовування розширеного вектора завдання X* = X* (t).П-регулятор стану в системі, що стежить, виробляє керуючий вплив, пропорційний векторувідхиленняe = Х*- X, тобто реалізує закон керування

U = Ke . (14.39)

Для одномірного об'єкта керуванняз вектором стану (14.35) вираження (14.39) можна переписати в скалярній формі

де x_i* = (y^{( i-1)})* .

ПІ-регулятор доповнює структуру системи інтегральними зв'язками:

Ефективна компенсація помилок, викликаних впливом, що обурює, F і змінами завдання Х* досягається використанням комбінованого керування (рис. 14.8)

U = Ke  L_XX*  L_FX_F , (14.42)

де L_X - матриця коефіцієнтів контуру прямих зв'язків по X*;

X* - розширений вектор завдання;

L_F - матриця коефіцієнтів контуру зв'язків по F;

X_F - вектор, складений зі збурювання F і його похідних.

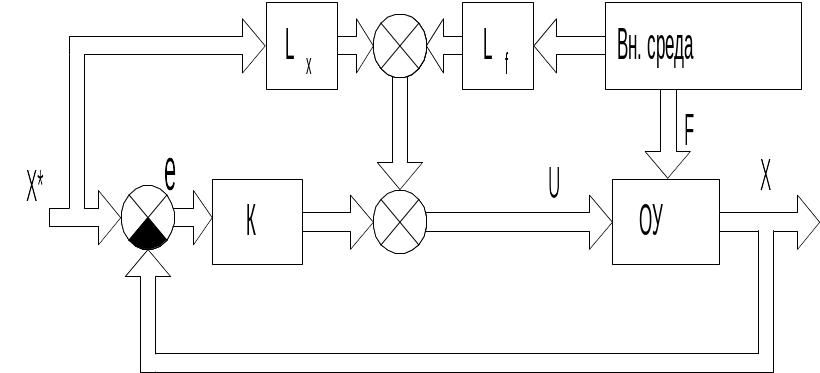
Рис. 14.8. Структурнасхемакомбінованоїсистеми

Параметрирегуляторів (коефіцієнтипрямихізворотнихзв'язків) визначаютьсяякфункціїпараметрів ( математичноїмоделіоб'єктакерування. Тому при керуванні нестаціонарним об'єктом виникає необхідність зміни параметрів регулятора в процесі роботи системи. Завдання настроювання регулятора ускладнюється, коли параметри об'єкта керування невідомі або неконтрольоване змінюються. Для керування такими об'єктами використовуються адаптивні регулятори, параметри яких настроюються за допомогою блоку адаптації (БА, рис. 14.9).

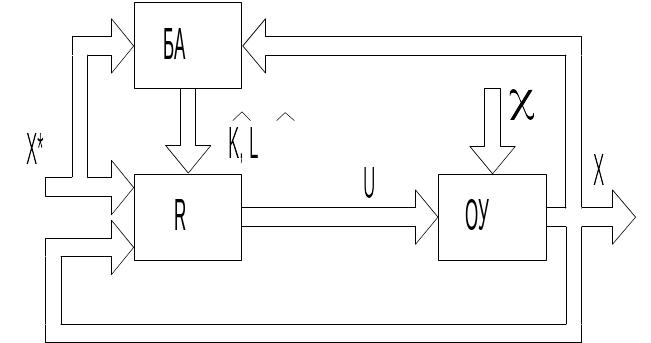
Рис. 14.9. Структурна схема адаптивної системи

Адаптивний регулятор стану комбінованого типу містить що настроюється контури, зворотних зв'язків по стану X і прямих зв'язків по розширеному вектору завдання X*. Закон керування такого регулятора

U = e X*, (14.43)

де , - матриці прямих і зворотних зв'язків зізмінними коефіцієнтами (параметрами).

Функції блоку адаптації полягають в автоматичному настроюванні параметрів регулятора (14.43).

У практиці адаптивних систем одержалипоширеннядва підходи до настроювання параметрів.

Перший з них передбачає включення до складу системи блоку ідентифікатора, що здійснює обчислення невідомих параметрів об'єкта керування. Тоді після визначення вектора  значення й можуть бути знайдені по відомим, підготовленим заздалегідь, залежностям

= () , = () . (14.44)

Другий підхід (безідентифікаційний) дозволяє здійснити настроювання контуру прямих зв'язківчастини регулятора (14.44). При цьому матриця зворотних зв'язків розраховується за номінальним значенням вектора  і залишаєтьсянезмінної = K₀. Як джерело інформації про параметричні помилки регулятора в блоці адаптації використовується сигнал зворотного зв'язка по відхиленню:

U_e = K₀e . (14.45)

Блок адаптації здійснює зміну параметрів регулятора доти, поки в системі не встановиться нульове значення сигналу зворотногозв'язка Ue і, отже, значення e буде рівнятисянулю.