12.6 Методи визначення якості регулювання нелінійних систем

Поблизу межі стійкості якість процесу регулювання погіршується, ця обставина дає вважати, що будь-який критерій стійкості може послужити основою для вироблення тих або інших оцінок якості процесу.

У лінійних системах всі критерії стійкості встановлюють нерівність, що дає умови знаходження всіх коренів характеристичного рівняння зліва від уявної осі. Як відомо, одним з таких показників є ступінь стійкості, але на практиці якість оцінюється за іншими прямими показниками якості, з якими встановлюється зв'язок через ступінь стійкості.

За допомогою критерію Попова поняття ступеня стійкості може бути використане і для нелінійних систем.

Говорять, що нелінійна система володіє загасанням або ступенем стійкості δ0 не менше заданої, якщо для відхилення процесу ξ(t) від вимушеного або відхилення координат від положення рівноваги при будь-яких t залишається справедливою нерівність

де М - const.

Щоб нерівність (12.47) могла мати місце при будь-яких t, необхідно, щоб

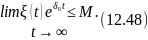
Якщо ця межа буде рівною нулю, тобто

,

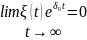то це означає, що

швидше, ніж

По аналогії з лінійними системами для оцінки якості нелінійної системи можна застосувати інтегральну квадратичну оцінку

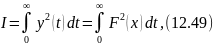
де у - вихідна координата нелінійного елементу.

У загальному вигляді визначити або оцінити величину інтеграла (12.49) не представляється можливим. Але, якщо накласти деякі обмеження на клас нелінійних функцій F(x), то оцінка величини інтеграла стає можливою.

Додаткове обмеження, що накладається на функцію F(x), зводиться до наступного.

Розглядається клас функцій, що задовольняють умові

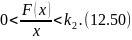
Дотична, проведена з початку координат F(x), має кутовий коефіцієнт k0, причому

k0<k2, і крива F(x) лежить нижче за дотичну в усіх точках, окрім точки дотику (рис. 12.8).

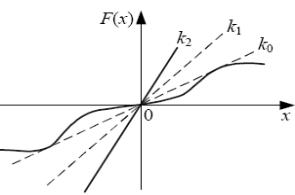
Рис. 12.8 Клас нелінійних функції

Для введення оцінки вибирається проміжний параметр k1, ув'язнений між k0 і k2:

причому

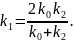
Оцінка:

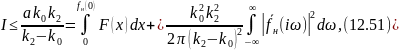
де fн - реакція лінійної частини на збурення початкових умов;

- перетворена по Фур’є;

α - вибирається як можна меншою, в крайньому разі це може бути кутовий коефіцієнт дотичної, проведеної з точки (-1/k0, і0) до видозміненої частотної характеристики системи.

Таким чином, оцінка (12.51) зводиться до виразу, який завжди може бути визначений шляхом інтегрування графіка функції F(x) в заданих межах і обчислення інтеграла

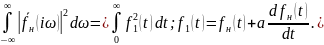
Оцінка (12.51) дає задовільні результати, якщо k1 достатньо відрізняється від k0. Якщо ці величини близькі, користуватися оцінкою не має сенсу.

12.7 Тренувальні завдання

1. У нелінійних системах досліджується стійкість руху. Розрізняють збурений рух і незбурений рух. Основними видами стійкості руху є поняття стійкості руху по Ляпунову і асимптотичній стійкості. Крім того для нелінійних систем існують такі поняття, як стійкість в "малому" і стійкість в "великому".

Для дослідження стійкості в "малому" використовується перший метод Ляпунова, який дозволяє судити про стійкість нелінійної системи по лінійній системі першого наближення.

А Який рух називається збуреним і який рух називається незбуреним?

В Який сенс має поняття стійкості руху системи по Ляпунову і чим воно відрізняється від асимптотичної стійкості?

С Які теореми були доведені Ляпуновим в першому методі дослідження стійкості в "малому" стану рівноваги нелінійної системи?

2. Як відомо, достатні умови стійкості нелінійних систем дає другий метод Ляпунова, що дозволяє досліджувати стійкість в "великому". Згідно цьому методу в розгляд вводиться функція V(у1, у2, ..., уn), задана у фазовому просторі і така, що володіє наступними властивостями: безперервна зі всіма своїми частковими похідними в деякій відкритій області, що містить початок координат; при у1 = у2 = ... = уn= 0 - V(у1, у2, ..., уn) = 0; усередині даної області V є знаковизначеною функцією, тобто V> 0 або V< 0.

А. М. Ляпуновим були сформульовані три теореми: про стійкість, про асимптотичну стійкість і про нестійкість. Так для доказу асимптотичної стійкості будується і досліджується похідна за часом функції Ляпунова, яка через систему диференціальних рівнянь, що описують нелінійну систему, повинна бути знаковизначеною функцією протилежного з V знаку.

Якщо знайти таку функцію V вдасться, то стійкість нелінійної системи буде доведена, причому стійкість в "великому". Єдиного підходу до побудови функції V(у1, у2, ..., уn) не існує, але є рекомендації по складанню цієї функції для дослідження певного класу систем.

А Яка теорема фізики лежить в основі другого методу Ляпунова?

В Якими властивостями повинна володіти функція Ляпунова і її похідна за часом, щоб нелінійна система була стійка ?

С Як Ви поясните, що другий метод Ляпунова дає стійкість нелінійної системи в "великому"?

3. Для дослідження стійкості певного класу нелінійних систем застосовують критерій абсолютної стійкості. Цей критерій відноситься до групи частотних критеріїв стійкості. Дана нелінійна система є замкнутою системою і складається з лінійної частини, що характеризується амплитудно-фазовою характеристикою W(iω), і нелінійного елементу із статичною характеристикою Ф(х) з підкласу (0, k), тобто 0 ≤ Ф(х)/х ≤ k, що стоїть в негативному зворотньому зв'язку.

Для стійкості стану рівноваги нелінійної системи із стійкою лінійною частиною достатньо виконання умови, що дійсна частина функцій Попова П(іω) позитивна.

А Як Ви розумієте абсолютну стійкість?

В Що є видозмінена амплитудно-фазова характеристика лінійної частини, і як остання пов'язана з початковою?

С Дайте геометричне трактування критерію абсолютної стійкості.

4. В нелінійних системах для дослідження якості регулювання використовують критерії стійкості, з яких виводять такий показник як ступінь стійкості. Також для оцінки якості регулювання використовують інтегральні критерії якості.

А В якому вигляді записується інтегральний квадратичний критерій?

В Які обмеження накладаються на нелінійну функцію у = F(x) при розрахунку інтегральних критеріїв?

С В яких випадках говорять, що нелінійна система володіє загасанням?