12.3 Методи побудови функції Ляпунова

Однією з основних проблем, що виникають при практичному використанні другого методу Ляпунова, є вибір функції Ляпунова. Загального методу вибору функції Ляпунова не існує, але все ж є деякі рекомендації по складанню цієї функції для дослідження певного класу систем. Найчастіше цю функцію вибирають у вигляді квадратичних форм.

12.3.1 Функція Ляпунова у вигляді квадратичних форм

Для лінійних систем функція Ляпунова є квадратичними формами координат, коефіцієнти яких знаходяться порівняно легко. Хай дана система диференціальних рівнянь

і хай корені її характеристичного рівняння ліві, тобто мають негативні дійсні частини. Шукатимемо коєфіцієнтиli,jквадратичної форми

так, щоб повна похідна цієї форми

була визначено-негативною.

Для цього, слідуючи Ляпунову, задамося визначено-позитивною формою

(12.24)

з коефіцієнтами gij = gji.

Таку форму можна вибрати таким чином: задаються n довільними речовими коефіцієнтами, g11, g22, ..., gnn і потім визначають

.

Тоді G(у) є повним квадратом

і є безумовно-позитивною функцією.

Ляпуновим було доведено, що при негативних дійсних частинах коренів характеристичного рівняння завжди можна єдиним чином підібрати коефіцієнти форми, яка буде визначено-позитивною. Оскільки dL/dt < 0, тоL є функцією Ляпунова. Ляпунов вказав наступний метод знаходження функції V для лінійних систем. Шукатимемо лінійну форму змінних

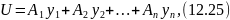
яка задовольняла б умові

Для знаходження коефіцієнтів А1, А2, ..., An підставимо (12.25) в останній вираз, в результаті отримаємо

Оскільки y1,y2, ...,ynнезалежні змінні, та рівняння може існувати лише за умови, що всі коефіцієнти при у1, у2,...,уп тотожно рівні нулю. Знаходимо

Умовою спільності цих n рівнянь є рівність нулю визначника системи ( Δ = 0), де χ є коренем характеристичного рівняння. Оскільки в загальному випадку їх п, то можна знайти п значень для функції U, рівних U1, U2, ..., Un. Оскільки корені можуть бути комплексними, тобто

,

то їм відповідають зв'язані значення функції і .

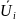Складемо далі функцію

якщо виявиться дійсною величиною, візьмемо Ui². Таким чином отримуємо додатно-визначену функцію, похідна за часом якою буде

де

Підставляючи в (12.29) значення dyi/dt з рівняння (12.21), зрештою отримуємо

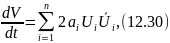
де αі - дійсні частини коренів.

Таким чином, вказано спосіб побудови функції Ляпунова для лінійної системи.

12.3.2 Побудова функції Ляпунова методом г. Сеге

Згідно цьому методу функція Ляпунова записується у вигляді

де коефіцієнти aijє функціями фазових координат уi, тобто aij(yi).

Похідна від функції Ляпунова за часом буде

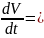
Роботу методу Г. Ceгe зручніше прослідкувати на прикладі систем другого порядку. В цьому випадку (12.31) прийме вигляд

Визначенню підлягають коефіцієнти а11(у1), а12(у1), а22(у2). Приймається, що а22(у2) = 1, тоді

і, отже, похідна (12.32) записується таким чином

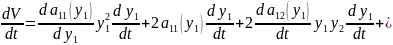(12.34)

Оскільки початкова нелінійна система другого порядку записується у вигляді

то похідна від функції Ляпунова через ці диференціальні рівняння буде

(12.35)

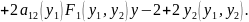
Припустимо, що права частина похідної функції Ляпунова є поліномом другого порядку відносно yk

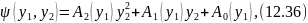
де A0, A1, А2- поліноми, залежні від у1.

Для забезпечення стійкості у всій області (y1, у2) необхідно зажадати, щоб рівняння ψ(y1, y2) = 0 мало кратні корені, умовою якого є рівність нулю дискримінанта: .

Згідно методу Г. Сеге приймається А2 = А1 = 0 і на підставі цього складається система диференціальних рівнянь для визначення коефіцієнтів а11, а12:

(12.37)

Далі необхідно вирішити систему диференціальних рівнянь (12.37) відносно а11,а12. Знайдені значення коефіцієнтів підставляються у вираз для функції Ляпунова і її похідної, після чого перевіряється знаковизначеність функції V(у1, у2) і визначається знак похідної dV/dt. На підставі отриманих результатів про знаковизначеність функції V(y1, y2) і знаку dV/dt робиться вивід про стійкість системи автоматичного управління по Ляпунову: система буде стійкою, якщо отримали, що V(y1, у2) > 0, а dV/dt < 0.