4. Розбиття на прості дроби

Як видно з прикладу 3.2, рішення диференціального рівняння, отримане з використанням перетворення Лапласа, є раціональним дробом. Для полегшення зворотного перетворення отриманий дріб необхідно розкласти на прості дроби, користуючись наступним правилом.

Дроб

(3.34)

називається правильним раціональним дробом, якщо порядок чисельника менший, ніж порядок знаменника. Для розкладання дробу (3.34) необхідно знайти корінь рівняння .

Якщо корінь дійсний, то йому відповідає дріб вигляду .

Якщо корені дійсні кратності то їм відповідає сума дробів

Якщо корені комплексно зв'язані, то

Якщо корені комплексно зв'язані кратності то

Таким чином, дріб (3.34) можна представити у вигляді

(3.35)

Коефіцієнти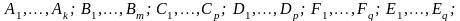 знаходяться методом невизначених множників. В цьому випадку права частина (3.35) приводиться до спільного знаменника і виходить рівність двох дробів, у яких знаменники рівні, отже, повинні бути рівні і чисельники. З рівності останніх складається система алгебраїчних рівнянь для визначення невідомих коефіцієнтів, яка вирішується відомими методами розв’язання лінійних алгебраїчних систем.

При визначенні оригіналу по отриманому зображенню користуються наступними формулами відповідності:

Приклад 3.3 Знайти оригінал, якщо зображення

Дане зображення розкладається на прості дроби:

Права частина останнього виразу приводиться до спільного знаменника, і з умови рівності чисельників отримують:

З рівності коефіцієнтів при відповідних степенях s в лівій і правій частинах записується система алгебраїчних рівнянь:

рішення якої дає Таким чином

Застосовуючи зворотне перетворення, записується вираз для оригіналу:

8. Передаточна функція

Одною з основних характеристик об'єкту управління, використовуваною в теорії автоматичного управління, є передаточна функція, записана в термінах перетворення Лапласа.

Передаточною функцією об'єкту називається відношення перетвореного по Лапласу виходу об'єкту 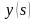до перетвореного по Лапласу входу за нульових початкових умов.

Передаточна функція визначається тільки внутрішніми властивостями системи, є функцією комплексного змінного і позначається:

	(3.36)
Рис. 3.13 Приклади різних об'єктів: а – з одним входом і одним виходом; б – двома входами і одним виходом; в – двома входами і двома виходами

Передаточна функція характеризує динаміку об'єкту тільки по певному каналу, що зв'язує конкретний вхід об'єкту і конкретний вихід (рис. 3.13).

Якщо об'єкт має декілька входів і виходів, то він характеризується декількома передаточними функціями, визначити які можна безпосередньо, користуючись визначенням (3.36).

Приклад 3.4 Хай на вхід об'єкту подається сигнал , а на виході знімається сигнал, що описується функцією

Для визначення передаточної функції необхідно визначити і тоді передаточна функція . Як і диференціальне рівняння, передаточна функція повністю характеризує динаміку лінійного об'єкту. Якщо задано диференціальне рівняння об'єкту, то для отримання передаточної функції необхідно перетворити диференціальне рівняння по Лапласу і з отриманого алгебраїчного рівняння знайти відношення .

У загальному випадку диференціальне рівняння об'єкту представляється у вигляді

(3.36, a)

де 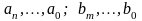– постійні коефіцієнти.

Після перетворення по Лапласу за нульових початкових умов отримують:

або

і тоді

(3.37)

Якщо відома передаточна функція об'єкту, то зображення виходу об'єкту дорівнює добутку передаточної функції на зображення входу :

(3.38)

Останній запис є не що інше, як загальна форма запису рішення диференціального рівняння в операторній формі.

Таким чином, передаточна функція дорівнює відношенню двох поліномів:

де

Для реальних фізичних об'єктів можна відзначити як характерну особливість той факт, що ступінь полінома завжди менше або рівна ступеню полінома 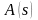, тобто , отже

.

Передаточна функція також взаємно пов'язана з часовими характеристиками.

Якщо є вираз для перехідної функції, отже, вхідний сигнал або вихідний сигнал або , і тоді передаточна функція дорівнює

(3.39)

Із (3.39) може бути отриманий вираз для перехідної функції через перетворення Лапласа

(3.40)

Якщо відомий вираз для вагової функції, то вхідний сигнал або , вихідний сигнал і, отже,

(3.41)

тобто вираз для передаточної функції є не що інше, як перетворення Лапласа від вагової функції.

Приклад 3.5 Нехай об'єкт описується диференціальним рівнянням . Знайти і .

Застосовуючи перетворення Лапласа: , визначаємо передаточну функцію .

Перехідна функція ; .

Вагова функція ; .
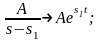
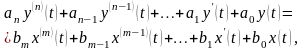