Примеры
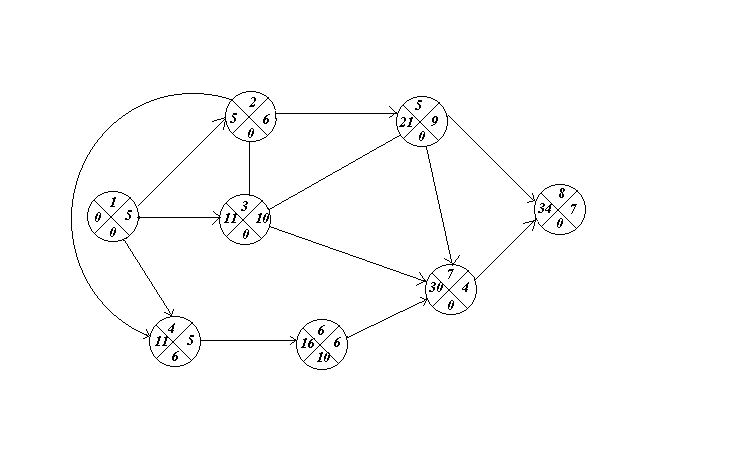
Пример. При анализе проекта разработки выяснилось, что она состоит из восьми работ, пронумеруем их от 1 до 8, продолжительность которых, соответственно, равны 5, 6, 10, 5, 9, 6, 4 и 7 неделям. Причем, работы 2, 3 и 4 могут выполняться после окончания работы № 1; работы 3, 4 не могут выполняться раннее выполнения работы №2; работа №5 может начаться только после выполнения работ №2 и 3; работа №6 выполняется только после выполнения работы №4; работа №7 может выполняться после окончания работ №3 и 5; выполнение работ №8 может начаться лишь после выполнения работ №5 и 7. Найти продолжительность выполнения разработки и критический путь ее выполнения.
Решение
Построим сетевой граф, используя исходные данные:
Вычислим временные характеристики графа:
t1=0;
t2=0+5=5 (к работе 2 ведет только один путь 1- 2);
К работе 3 ведут два пути 1: 1 – 3----- t3=0+5=5;
2: 1 – 2 – 3-----t3=5+6+11.
max t3=11. Следовательно, t3=11: выполнение работы №3 может начаться лишь через 11 недель.
Раннее время каждой из остальных работ определится совершенно аналогично. Полученные результаты сведем в таблицу 9.
Таблица 9 - Расчет раннего времени наступления работы
Номер работы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Номера последую-щих работ |
2,3,4 |
3,4,5 |
5,7 |
5 |
7,8 |
7 |
8 |
- |
di |
5 |
6 |
10 |
5 |
9 |
6 |
4 |
7 |
ti |
0 |
5 |
11 |
11 |
21 |
16 |
30 |
34 |
Продолжительность разработки Т = 34 + 7 = 41.
Построим обратный граф для вычисления временных характеристик i:
Вычислим временные характеристики обратного графа:
8=0; 7=7; 5=11,...
Полученные результаты сведем в таблицу 10.
Таблица 10 - Расчет раннего времени наступления работ в обратном графе
Номер работы |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Номера последую-щих работ |
5,7 |
3,5,6 |
4 |
2,3 |
1,2 |
1,2 |
1 |
- |
di |
7 |
4 |
6 |
9 |
5 |
10 |
6 |
5 |
|
0 |
7 |
11 |
11 |
17 |
20 |
30 |
36 |
Продолжительность разработки Т = 36 + 5 =41.
Для определения величин mi и zi составим таблицу 11.
Таблица 11 - Расчет полного запаса времени
Номер работы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
di |
5 |
6 |
10 |
5 |
9 |
6 |
4 |
7 |
ti |
0 |
5 |
11 |
11 |
21 |
16 |
30 |
34 |
|
36 |
30 |
20 |
17 |
11 |
11 |
7 |
0 |
mi |
41 |
41 |
41 |
33 |
41 |
33 |
41 |
41 |
zi |
0 |
0 |
0 |
8 |
0 |
8 |
0 |
0 |
Из таблицы 11 видно, что запаса времени нет (zi=0) у работ 1, 2, 3, 5, 7, 8. Таким образом, критическим является путь
1—2---3---5---7---8.
На этом планирование выполнения работ заканчивается, и начинается процесс управления выполнением разработки.