2.5. Производные высших порядков

Производная данной функции у = f (x), если она су­ществует, называется производной первого порядка и представляет собой некоторую новую функцию. Производная от производной первого порядка называется производной второго порядка, или второй произ­водной, и обозначается так:

, или , или .

Аналогично, если существует производная от производной второ­го порядка, то она называется производной третьего порядка, или третьей производной, и обозначается так:

, или , или .

Производная от производной (n — 1) порядка называется производ­ной n-го порядка и обозначается

, или , или .

Формулы для вычисления производной второго порядка функций заданных неявно и в параметрической форме:

1. Неявно заданная функция F ( x, y) = 0.

Так как

,

то

.

2. Функция задана параметрически

Так как

,

то

, или .

Пример. Для функции найти .

Решение. Дифференцируя функцию , получим первую производную

,

дифференцируя функцию , получим вторую производную

.

Следовательно,

.

Пример. Для функции найти .

Решение. Дифференцируя функцию , получим первую производную

,

дифференцируя функцию , получим вторую производную

,

дифференцируя функцию , получим третью производную

.

Следовательно,

.

Пример. Для функции найти .

Решение. Дифференцируя функцию , получим первую производную

.

Дифференцируя функцию , получим вторую производную

.

Дифференцируя функцию , получим третью производную

.

Дифференцируя функцию , получим четвёртую производную

.

При сравнении найденных производных прослеживается закономерность, на основании которой можно сделать вывод, что

.

Значит,

.

Пример. Найти производную второго порядка функции .

Решение. Функция задана неявно F ( x, y) = 0, поэтому

.

Найдем .

.

Подставим найденные значения в формулу

Следовательно,

Производную второго порядка можно найти как производную от производной первого порядка. Дифференцируем по х обе части равенства, учитывая, что у есть функция от х, получим

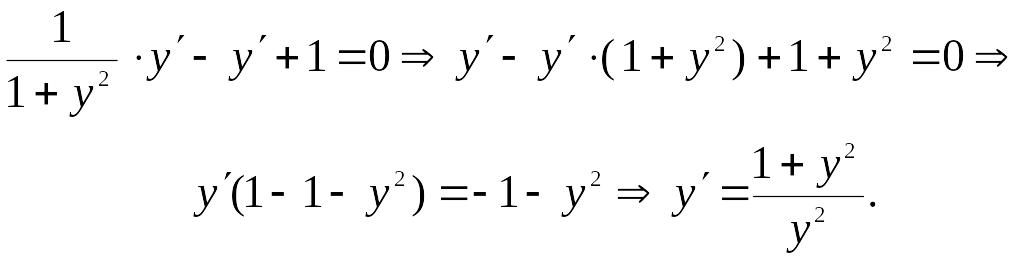
Находим производную от производной первого порядка

Подставим в выражение производной первого порядка

.

Тогда,

Следовательно,

Пример. Найти производную второго порядка функции, если .

Решение. Функция задана параметрически, поэтому

.

Найдем .

.

Подставим найденные значения в формулу

Следовательно,

Производную второго порядка можно найти как производную от производной первого порядка.

Найдем производную первого порядка :

.

.

Так как

,

то

Окончательно получим

6. Применение второй производной в задачах механики

Пусть s = s (t) — эта функция задает закон прямолинейного движения матери­альной точки. Мгновенная скорость v этого движения есть

v (t) = s'(t).

Если теперь эту скорость рассматривать как функцию времени, то производная от v есть ускорение а в момент t. Следовательно,

а(t) = s"(t).

Пример. Точка совершает прямолинейное колебательное движение по закону . Найти ускорение движения в момент времени .

Решение. Найдем скорость движения точки :

.

Зная скорость движения точки, найдем её ускорение :

.

Следовательно,

.

Пример. Скорость прямолинейного движения тела пропорциональна квадратному корню из пройденного пути s. Доказать, что тело движется под действием постоянной силы.

Решение. По условию имеем

, ( ;

отсюда

.

Но по закону Ньютона сила

, ( .

Следовательно,

Упражнения

1. Для функции найти .

2. Для функции найти .

3. Для функции найти .

4. Доказать, что для функции справедливо равенство .

5. Найти производную второго порядка от функции, заданной параметрически

6. Найти производную второго порядка от функции, заданной параметрически

7. Найти производную второго порядка от неявно заданной функции

8. Найти производную второго порядка от неявно заданной функции .

9. Путь тела, движущегося прямолинейно, определяется формулой (м). В какой момент времени t (c) ускорение будет

равно 14 ?

10. Показать, что если тело движется по закону , то его ускорение численно равно пройденному пути.