Предел функции
Определение. Число а называется пределом последовательности
,
если для всякого сколь угодно малого
положительного числа ε
найдется такое положительное число
N,
что │xn
-
a│<
ε
при n
> N.
В этом случае пишут
.
Определение.
Число А
называется пределом функции f
(х)
при x
→ а,
если для любого сколь угодно малого ε
> 0 найдется такое
> 0, что | f
(х)
— А
│ < ε
при
0 < │x
-
a│<
.
Условная
запись имеет вид:
Аналогично
,
если | f
(х)
— А
│ < ε
при │x│>
N.
Условно
записывают
,
если | f
(х)│
> М
при
,
где М
—
произвольное положительное число.
В
этом случае функция f
(х)
называется бесконечно большой при
.
Если
,
то функция
(x)
называется бесконечно малой,
при .
Бесконечно малую функцию также называют бесконечно малой величиной, или просто бесконечно малой.
Определение.
Функция
называется ограниченной на интервале
,
если существует число М
>
0 такое, что для всех
выполняется неравенство
.
Определение.
Функция
называется ограниченной при
,
если существуют числа М
>
0 и
такие, что при условии
выполняется неравенство
.
Свойства бесконечно малых функций:
Если функции
и
являются бесконечно малыми, то функция
также есть бесконечно малая.Произведение ограниченной при функции на бесконечно малую есть функция бесконечно малая.
Произведение постоянной на бесконечно малую есть бесконечно малая.
Произведение двух бесконечно малых есть бесконечно малая.
Сравнение бесконечно малых
Пусть α (x) и β (x) – бесконечно малые при x → а.
Если
,
то α
является бесконечно малой высшего
порядка
по сравнению с β. Запись: α = 0 ( β ).
Если
,
где k–
число, отличное от нуля, то α
и β
- бесконечно малые одного и того же
порядка. В частности, если
,то
бесконечно малые α
и β
называются эквивалентными и обозначаются
α
~ β
.
Если
→
∞, то это означает, что
= 0. Таким образом, β
является бесконечно малой высшего
порядка по сравнению с α,
т. е. β
= 0 (α).
3.Если α k и β – бесконечно малые одного и того же порядка, причем k > 0, то бесконечно малая β имеет порядок k по сравнению с α.
Отметим некоторые свойства бесконечно малых:
1°. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с каждым множителем, т. е. если γ = α β, то γ = 0(α) и γ = 0 (β).
2°.
Бесконечно малые
и
эквивалентны тогда и только тогда, когда
их разность α - β = γ является бесконечно
малой высшего порядка по сравнению c
α и β, т. е. если γ = 0(α), γ = 0 (β), то α
~
β.
3°.
Если отношение двух бесконечно малых
имеет предел, то этот предел
не
изменится при замене каждой из бесконечно
малых эквивалентной ей бесконечно
малой, т. е. если
,
α
~ α1
, β
~ β
1,
то
.
При решении примеров часто используется эквивалентность следующих бесконечно малых: если x → 0, то
sin х ~ х, tg х ~ х, arcsin х ~ x, arctg x ~ x, ln (1 + x) ~ х,
~
,
~
,
~
.
Если х < а и х → а, то употребляют запись х → a - 0; если х > а и х → а – запись х→ a + 0.
Числа
f
(а
- 0)
=
и f
(а
+
0) =
называются соответственно левым и
правым пределом функции f
(x)
в точке а.
Для существования предела функции f (х) при х → а необходимо и достаточно, чтобы f ( а - 0) = f ( а + 0).
Практическое вычисление пределов основывается на следующих теоремах:
.
Следствие из теоремы о пределах
.
Используются также следующие пределы:
(первый
замечательный предел);
=
= е
(второй замечательный предел),
где
е
2,7172….
Пример.
Найти предел функции
.
Решение.
Выполним непосредственную подстановку.
Используя теоремы о пределах и подставляя
в выражение предельное значение аргумента
,
получим
.
Пример.
Найти предел функции
.
Решение.
.
При
непосредственной подстановке предельного
значения аргумента функция
представляет
отношение двух бесконечно малых величин,
т. е. имеет место неопределенность вида
.
При раскрытии неопределенности
воспользовались формулой сокращенного
умножения
и делением числителя и знаменателя
дроби на
.
Пример.
Найти предел функции
Решение.
.
При
непосредственной подстановке предельного
значения аргумента функция
представляет
отношение двух бесконечно малых величин,
т. е. имеет место неопределенность вида
.
При раскрытии неопределенности
воспользовались формулой разложения
квадратного трехчлена на множители
,
где
корни квадратного трехчлена и делением
числителя и знаменателя дроби на
.
Пример.
Найти предел функции
Решение.
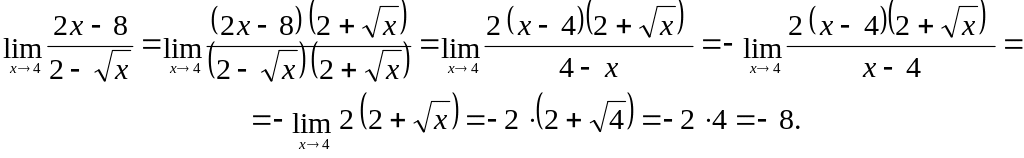При
непосредственной подстановке предельного
значения аргумента функция
представляет
отношение двух бесконечно малых величин,
т. е. имеет место неопределенность вида
.
При раскрытии неопределенности сначала
освободились от иррациональности в
знаменателе дроби, домножив числитель
и знаменатель на
,
затем в числителе вынесли за скобку
множитель 2, а в знаменателе воспользовались
формулой сокращенного умножения
.
Разделили числитель и знаменатель на
,
предварительно вынеся « - » за знак
предела и изменив знаки слагаемых
знаменателя на противоположные.
Пример.
Найти предел функции
.
Решение.
.
При непосредственной подстановке предельного значения аргумента функция представляет отношение двух бесконечно малых величин, т. е. имеет место неопределенность вида . Вначале умножили числитель и знаменатель дроби на 4, по следствию о вынесении постоянного множителя за знак предела
,
4 вынесли за знак предела и использовали первый замечательный предел
.
Пример.
Найти предел функции
.
Решение.
.
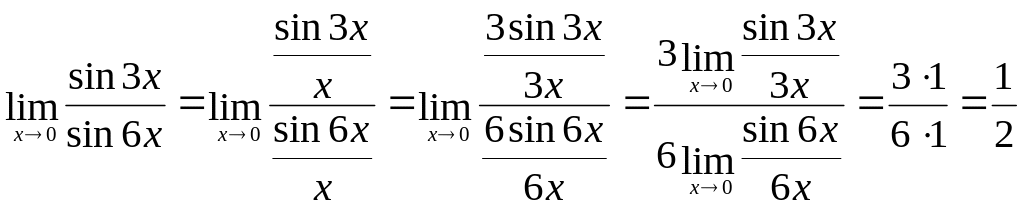При
непосредственной подстановке предельного
значения аргумента функция
представляет
отношение двух бесконечно больших
величин, т. е. имеет место неопределенность
вида
.
Разделили числитель и знаменатель дроби
на
и применили теорему о пределе частного
.
Пример.
Найти предел функции
Решение.
.
При
непосредственной подстановке предельного
значения аргумента функция
представляет
отношение двух бесконечно больших
величин, т. е. Имеет место неопределенность
вида
.
При раскрытии неопределенности разделили
числитель и знаменатель дроби на
(в любом случае делим на наивысшую
степень х,
содержащуюся в числителе или знаменателе)
и приняли во внимание, что
(величина, обратная бесконечно большой,
есть величина бесконечно малая, а предел
бесконечно малой величины равен нулю).
Пример.
Найти предел функции
Решение.
.
При
непосредственной подстановке предельного
значения аргумента функция
представляет
отношение двух бесконечно больших
величин, т. е. имеет место неопределенность
вида
.
При раскрытии неопределенности разделили
числитель и знаменатель дроби на
и приняли во внимание, что
.
Пример.
Найти предел функции
Решение.
При
непосредственной подстановке предельного
значения аргумента функция
представляет
произведение бесконечно малой и
бесконечно большой величины, т. е. имеет
место неопределенность вида
.
При раскрытии неопределенности
использовали формулу тригонометрии
,
теорему
о пределе произведения
,
теорему о пределе частного
и первый замечательный предел
.
Пример.
Найти предел функции
Решение.
При непосредственной подстановке
предельного значения аргумента функция
представляет
разность бесконечно больших величин,
т. е имеет место неопределенность вида
.
Для раскрытия неопределенности привели
дроби к общему знаменателю, привели
подобные слагаемые в числителе и
разделили числитель и знаменатель дроби
на
.
Пример.
Найти предел функции
.
Решение.
При непосредственной подстановке
предельного значения аргумента функция
представляет
степень, основание которой стремиться
к 1, а показатель стремится к бесконечности,
т. е. имеет место неопределенность вида
.
Для
применения второго замечательного
предела
=
е
преобразуем выражение, стоящее в скобках,
к виду
:
=
.
Пусть
,
тогда
.
Если
,
то
.
Выразим предел функции через переменную n:
Также использовали теорему о пределе произведения функций
и следствие из теоремы о пределах
.
Пример.
Найти предел функции
.
Решение. При непосредственной подстановке предельного значения аргумента функция представляет степень, основание которой стремиться к 1, а показатель стремится к бесконечности, т. е. имеет место неопределенность вида .
Для
применения второго замечательного
предела
=
е
выполним преобразование: пусть
,
тогда если
,
то
Выразим предел функции через переменную n:
.
Также использовали следствие из теоремы о пределах
.
Пример. С помощью замены эквивалентных величин найти предел
.
Решение. Используя эквивалентность бесконечно малых
sin х ~ х и ln (1 + x) ~ х,
получим
Пример. С помощью замены эквивалентных величин найти предел
.
Решение. Используя эквивалентность бесконечно малых
ln
(1 + x)
~ х,
~
и
~
,
получим
Упражнения
Найти пределы следующих функции:
1.
а)
;
б)
.
2.
а)
;
б)
.
3.
а)
;
б)
.
4.
а)
;
б)
.
5.
а)
;
б)
.
6.
а)
;
б)
.
7.
а)
;
б)
.
С помощью замены эквивалентных величин найти следующие пределы:
8.
а)
;
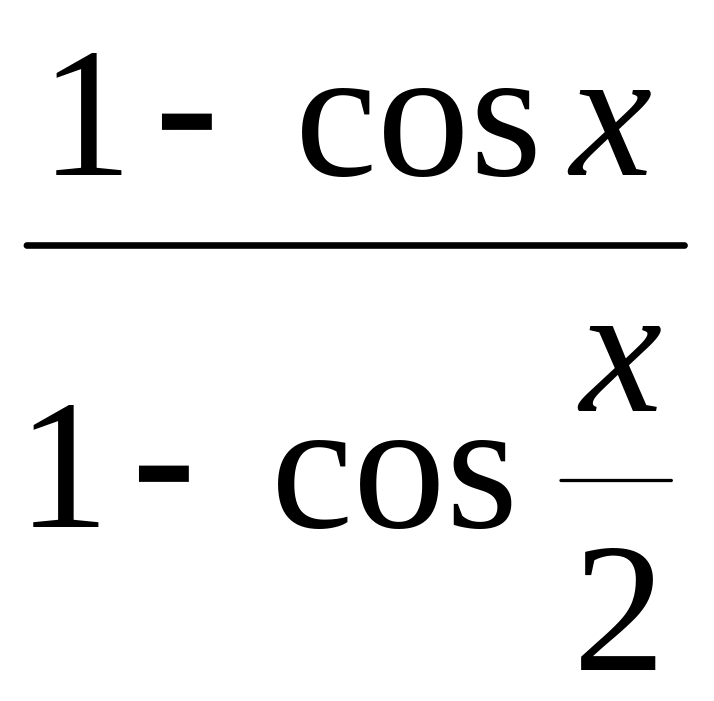б)
.