
- •Дифференциальное исчисление функций одной переменной в упражнениях и задачах.
- •Глава 1. Введение в анализ
- •Определение функции
- •Предел функции
- •1.3. Непрерывность функций
- •Глава 2. Дифференциальное исчисление функции одной переменной
- •2. 1. Задачи, приводящие к понятию производной
- •2.2. Определение производной
- •2.3. Дифференцирование функций
- •2.4. Приложения производной к задачам геометрии и механики.
- •2.5. Производные высших порядков
- •Применение второй производной в задачах механики
- •Дифференциал функции
- •2.8.Основные теоремы о дифференцируемых функциях
- •2.9.Раскрытие неопределенностей. Правило Лопиталя
- •2.9. Исследование функций с помощью производных
- •2.10. Локальный экстремум функции
- •2.11.Наибольшее и наименьшее значения функции
- •2.12. Выпуклость кривой. Точки перегиба
- •2.13. Асимптоты графика функции
- •2.14. Общая схема исследования функции
- •2.15. Формула Тейлора
- •2.16.Векторная функция скалярного аргумента
- •2.17.Дифференциал длины дуги
- •2.18.Кривизна
- •Радиус, центр и круг кривизны. Эволюта и эвольвента
- •Литература
- •Содержание
- •Глава 1. Введение в анализ………………………………………3
- •1.1. Определение функции………………………………………………….3
- •Глава 2. Дифференциальное исчисление функции одной переменной………………………………………………………..28
1.3. Непрерывность функций
Функция f (х) называется непрерывной в точке а, если:
1) эта функция определена в точке а и некоторой её окрестности;
2)
существует конечный предел
![]() ;
;
3)
этот предел равен значению функции в
точке а,
т. е.
![]()
Обозначим
x
– a
=∆x
(приращение
аргумента) и f
(х)
– f
(а)
= ∆y
(приращение
функции), тогда условие непрерывности
можно записать так:
![]() ,
т .е. функция f
(х)
непрерывна в точке а
тогда
и только тогда,
когда в этой точке бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции.
,
т .е. функция f
(х)
непрерывна в точке а
тогда
и только тогда,
когда в этой точке бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции.
Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т. п.), то она называется непрерывной в этой области.
Точка а, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции.
Если существуют конечные пределы
![]()
![]() и
и
![]() ,
,
причем не все три числа f (а), f (а - 0), f (а + 0) равны между собой, то а называется точкой разрыва I рода.
Точки разрыва I рода подразделяются на точки устранимого разрыва (когда f (а - 0) = f (а + 0) f (а), т. е. когда левый и правый, пределы функции в точке а равны между собой, но не равны значению функции в этой точке) и на точки скачка (когда f (а - 0) f (а + 0), т. е. когда левый и правый пределы функции в точке а различны); в последнем случае разность f (а + 0) - f (а - 0) называется скачком функции в точке а. Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода. В точках разрыва II рода не существует хотя бы один из односторонних пределов, либо один из этих пределов бесконечный.
Теорема.
Если
функции f1
(х)
и f2
(х)
непрерывны
в точке х0,
то
непрерывны в этой точке также их
алгебраическая сумма f1
(
х)
±
f2
(
х),
произведение
![]() и,
при условии
f2
(
х)
≠ 0,
частное
и,
при условии
f2
(
х)
≠ 0,
частное
![]() .
.
Теорема. Если функция и = φ (х) непрерывна в точке х0, а функция у = f (u) непрерывна в точке и0 = φ (x0), то сложная функция у = f (φ (x)) непрерывна в точке х0.
Пример.
Используя
определение непрерывности, доказать,
что функция
![]() непрерывна
в точке
х
= 2.
непрерывна
в точке
х
= 2.
Решение.
Найдем предел функции
![]() при
при
![]() :
:
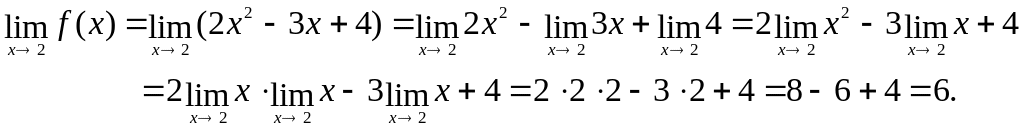
При нахождении предела функции использовали теоремы о пределах:
;
![]() ;
;
![]() ;
.
;
.
Вычислим значение функции в точке х = 2:
![]()
Таким
образом,
![]() =
=
![]() ,
следовательно,
функция
непрерывна
в точке
х
= 2.
,
следовательно,
функция
непрерывна
в точке
х
= 2.
Пример.
Показать,
что функция
![]() непрерывна
в точке
х =
непрерывна
в точке
х =![]() .
.
Решение.
Функция определена при
![]() .
Функции
.
Функции
![]() непрерывны в точке
х =
,
используя теоремы о непрерывных
функциях, функция
непрерывна
в точке
х =
.
непрерывны в точке
х =
,
используя теоремы о непрерывных
функциях, функция
непрерывна
в точке
х =
.
Пример.
Исследовать
функцию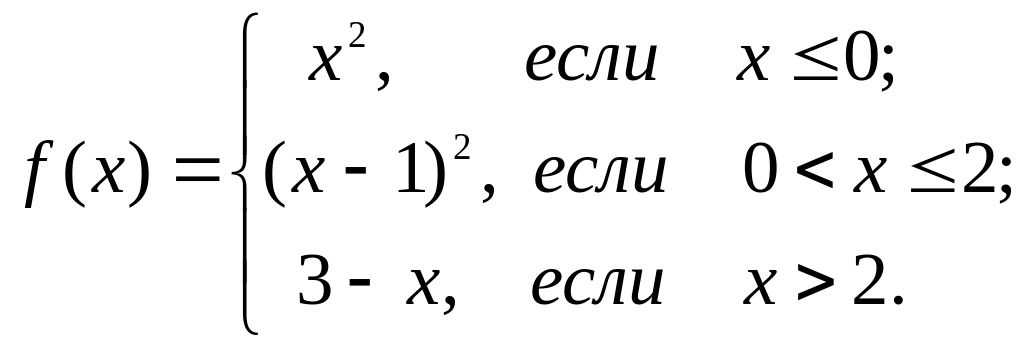 на непрерывность. Сделать схематический
чертеж.
на непрерывность. Сделать схематический
чертеж.
Решение.
Функция
определена и непрерывна на интервалах
![]() и
и
![]() ,
где она задана непрерывными элементарными
функциями.
,
где она задана непрерывными элементарными
функциями.
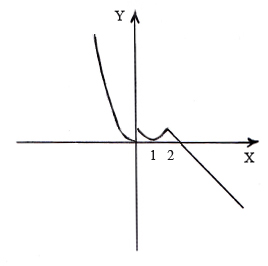
Следовательно, разрыв функции возможен только в точках х = 0 и х = 2, в которых меняется её аналитическое выражение.
Исследуя точку х = 0, найдем односторонние пределы функции при стремлении аргумента к этой точке слева и справа:
![]()
![]()
Так
как
![]()
![]() и
и
![]() ,
то функция
в точке
х
= 0 имеет разрыв первого рода (скачок -
,
то функция
в точке
х
= 0 имеет разрыв первого рода (скачок -
![]()
![]() ).
).
Исследуя точку х = 2, найдем односторонние пределы функции при стремлении аргумента к этой точке слева и справа:
![]()
![]()
Так как
![]() и
и
![]() ,
,
то функция в точке х = 2 не имеет разрыва, т. е. функция непрерывна.
Сделаем схематический чертеж
Пример.
Исследовать
функцию![]() на непрерывность. Сделать схематический
чертеж.
на непрерывность. Сделать схематический
чертеж.
Решение.
Функция
определена и непрерывна на интервалах
![]() и
и
![]() .
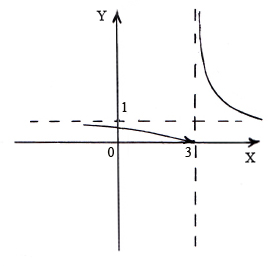
Следовательно, в
точке
х
= 3 функция
имеет разрыв.
.
Следовательно, в
точке
х
= 3 функция
имеет разрыв.
Определим характер разрыва. Найдем односторонние пределы функции при стремлении аргумента к этой точке слева и справа:
![]() .
.
![]() .
.
Таким образом, в точке х = 3 функция имеет разрыв второго рода, т. к. односторонние пределы функции при стремлении аргумента к данной точке слева и справа различны и один из них равен бесконечности.
Для
построения графика выясним поведение
функции
при
![]() :
:
![]() .
.
Значит, прямая у = 1 является горизонтальной асимптотой.
Сделаем схематический чертеж
Упражнения
Используя определение непрерывности, доказать, что функция
 непрерывна
в точке
х
= 3.
непрерывна
в точке
х
= 3.Исследовать функцию
 на непрерывность и найти точки разрыва.
на непрерывность и найти точки разрыва.Исследовать функцию
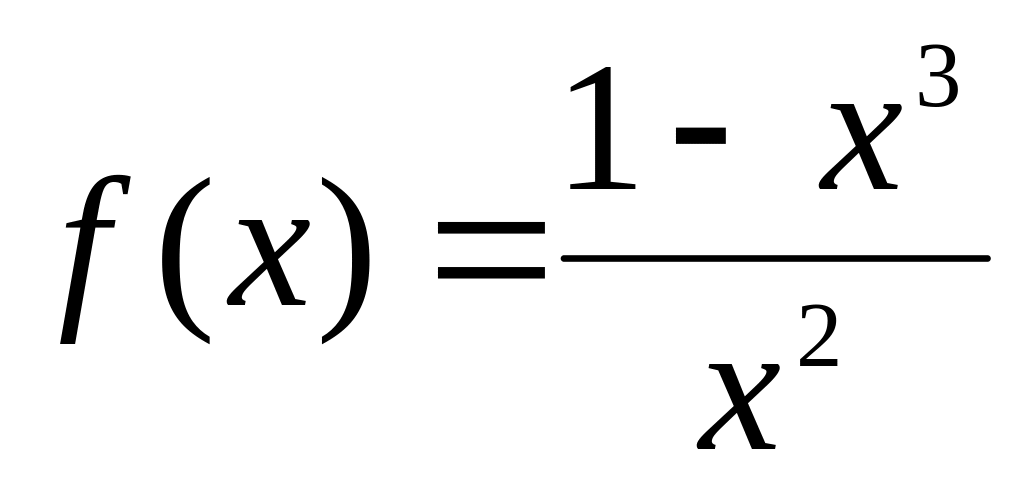 на непрерывность и найти точки разрыва.
на непрерывность и найти точки разрыва.
Исследовать функцию
 на непрерывность. Сделать схематический
чертеж.
на непрерывность. Сделать схематический
чертеж.Исследовать функцию
 на непрерывность. Сделать схематический
чертеж.
на непрерывность. Сделать схематический
чертеж.Исследовать функцию
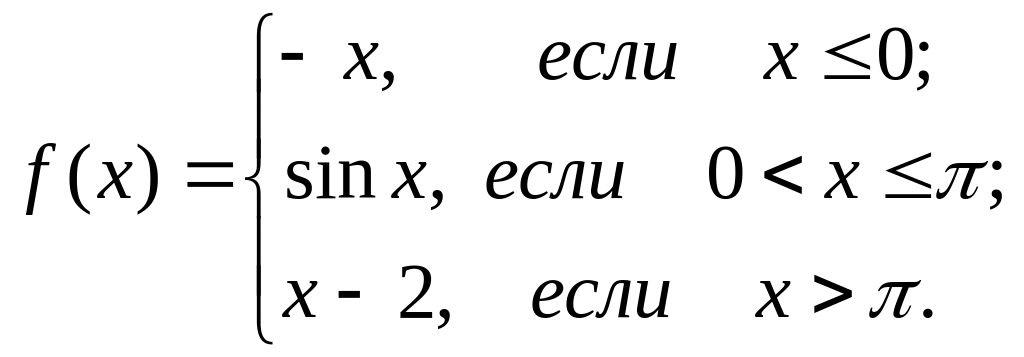 на непрерывность. Сделать схематический
чертеж.
на непрерывность. Сделать схематический
чертеж.Исследовать функцию
 на непрерывность. Сделать схематический
чертеж.
на непрерывность. Сделать схематический
чертеж.
