Радиус, центр и круг кривизны. Эволюта и эвольвента
Радиусом
кривизны называется величина, обратная
кривизне, т. е.
.
Если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением
,
то радиус кривизны
выражается формулой
.
Eсли плоская кривая отнесена к прямоугольной системе координат и задана параметрически системой уравнений , то радиус кривизны выражается формулой
,
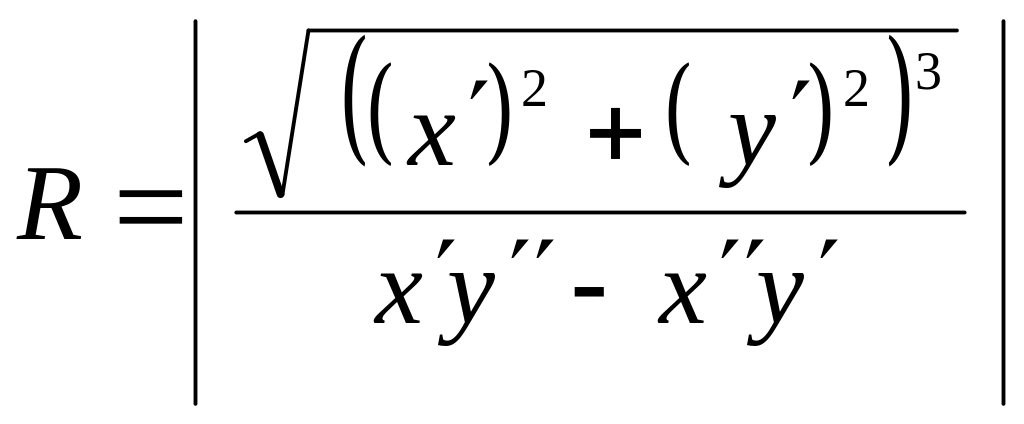где
,
,
,
.
Если плоская кривая отнесена к полярной системе координат и задана уравнением , то радиус кривизны выражается формулой
,
где , .
Окружностью
кривизны данной линии её точке А
называется
предельное положение окружности,
проходящей через три точки A,
B,
C
кривой, когда
и
.
Радиус окружности кривизны равен радиусу кривизны. Центр окружности кривизны называется центром кривизны и находится на нормали к линии, проведенной в точке А в сторону вогнутости этой линии.
Координаты
и
центра кривизны линии
вычисляются по формулам:
,
.
Эволютой линии называется множество её центров кривизны, а сама линия относительно своей эволюты называется эвольвентой.
Формулы для координат центра кривизны можно рассматривать как параметрические уравнения эволюты, где параметром является абсцисса х исходной линии.
Данная линия может иметь лишь одну эволюту, но у данной эволюты существует бесконечное множество эвольвент.
Пример.
Найти
радиус кривизны линии
в
точке с абсциссой
.
Решение. Найдем значения производных первого и второго порядков функции в точке с абсциссой :
,
.
Подставим
найденные значения
и
в
формулу
:
.
Следовательно, радиус кривизны линии в точке с абсциссой
.
Пример.
Найти
радиус кривизны линии
в
точке
.
Решение. Дифференцируя по t, получим
,
,
,
.
Вычислим значения производных в точке :
,
.
Подставляя найденные значения
,
в формулу
,
имеем
Следовательно, радиус кривизны линии в точке с абсциссой
Пример.
Найти
радиус кривизны кардиоиды
в
любой её точке.
Решение. Найдем
и :
.
Подставим найденные выражения в формулу
:
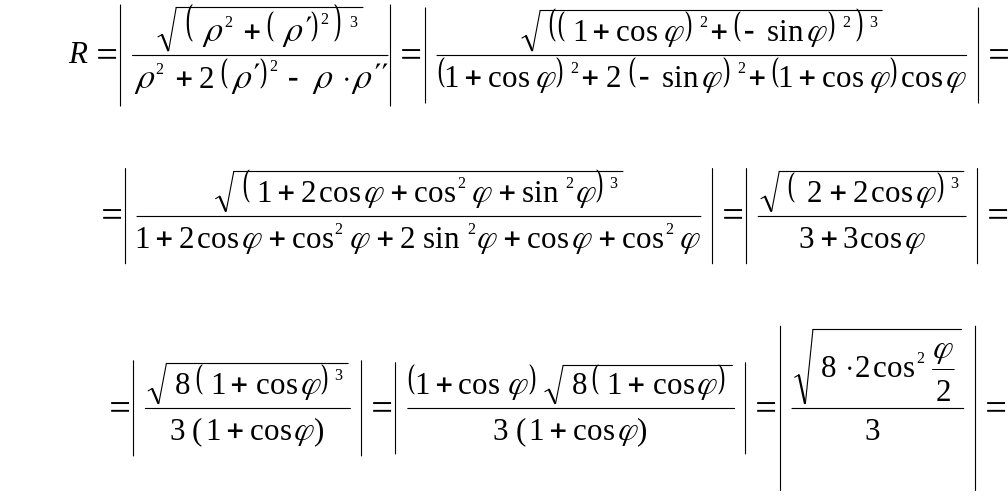
Следовательно, радиус кривизны кардиоиды в любой её точке
Пример.
Найти
координаты
и
центра кривизны линии
в
точке
.
Решение. Найдем значения производных первого и второго порядков функции в точке с абсциссой :
,
.
Подставим
значения
,
и найденные
значения
и
в
формулы
, :
,
Следовательно,
координаты
центра кривизны линии
в
точке
и
Пример.
Составить
уравнение эволюты кривой
.
Решение. Продифференцируем дважды уравнение параболы:
;
.
Так
как
,
то
.
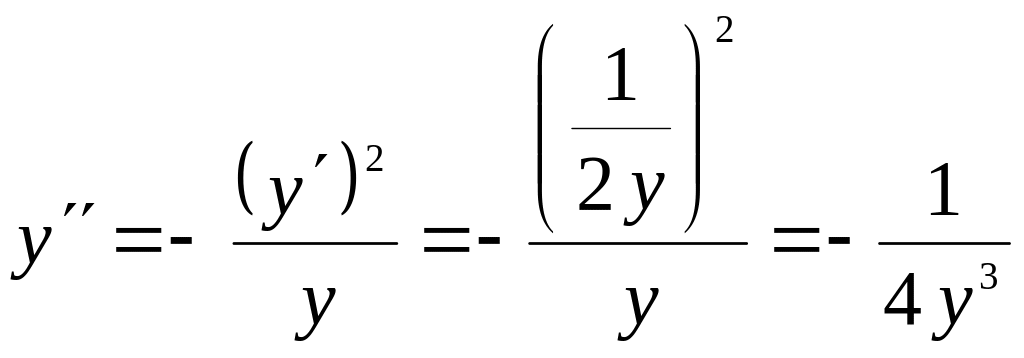Найдем координаты и центра кривизны линии , предварительно выразив х из уравнения :
.
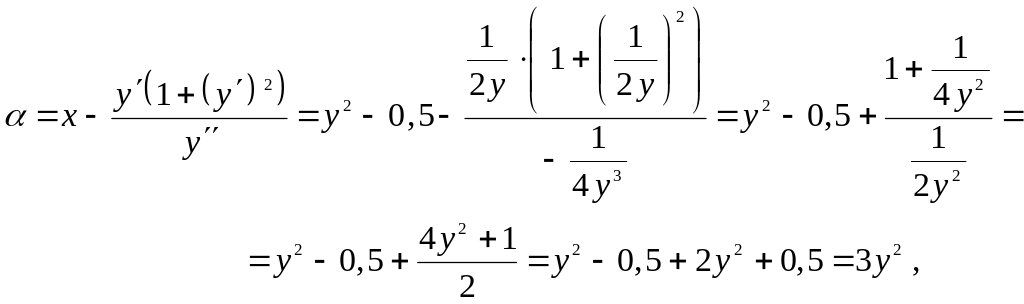
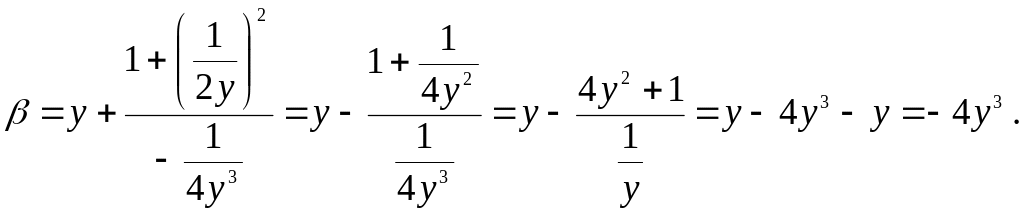
Имеем
-
уравнение эволюты в параметрической
форме. Выразим параметр у
из
и
:
;
.
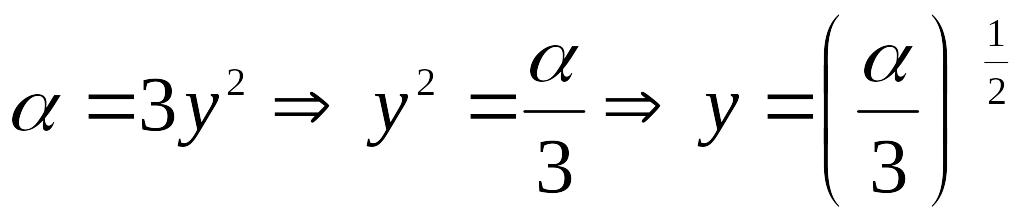Окончательно получаем,
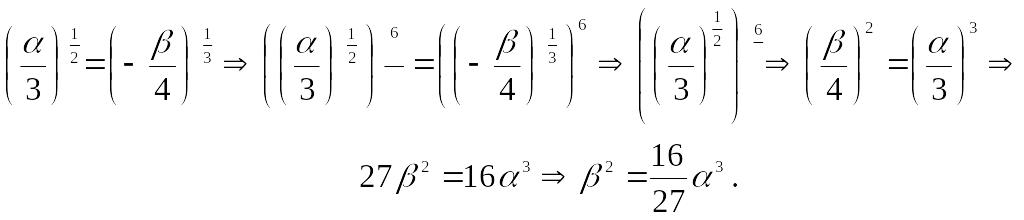
Следовательно,
уравнение
эволюты кривой
имеет вид
(уравнение полукубической параболы).
Упражнения
1.
Найти радиус кривизны линии
в
точке A:
а)
,
A
(
2; 2 ), б)
,
A
(
0; 1 ) .
2.
Найти радиус кривизны трехлепестковой
розы
, при
.
3.
Найти координаты
и
центра кривизны линии
в
точке A:
а)
,
A
(
1; 1 ), б)
,
A
(
1; 0 ) .
4. Составить уравнение эволюты кривой :
а)
,
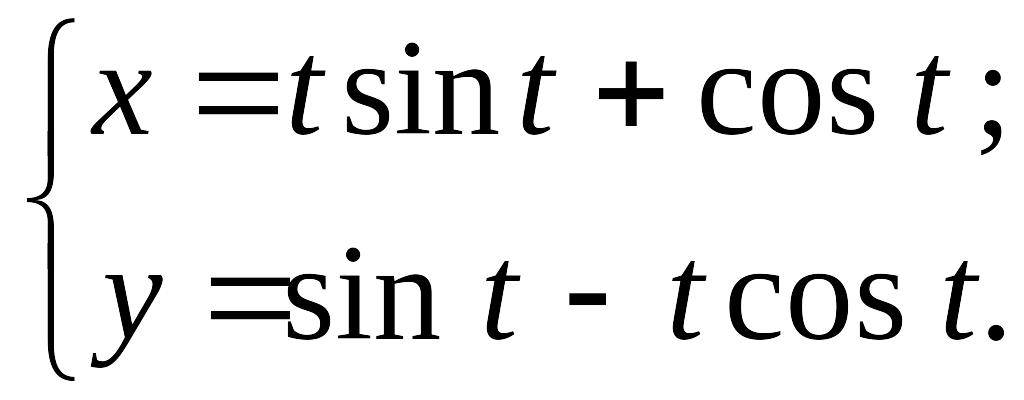б)
.