2.17.Дифференциал длины дуги

Пусть некоторая кривая на заданном промежутке является гладкой кривой, т. е. её производная непрерывна, тогда:

если плоская кривая отнесена к прямоугольной системе координат и задана уравнением , то дифференциал длины дуги dl выражается формулой

;

если плоская кривая отнесена к прямоугольной системе координат и задана уравнением , то дифференциал длины дуги dl выражается формулой

;

если плоская кривая отнесена к прямоугольной системе координат и задана параметрически системой уравнений , то дифференциал длины дуги dl выражается формулой

,

где , ;

если плоская кривая отнесена к полярной системе координат и задана уравнением , то дифференциал длины дуги dl выражается формулой

,

где .

С геометрической точки зрения дифференциал длины дуги можно представить длиной соответствующего отрезка касательной к линии в начальной точке дуги.

Пример. Найти дифференциал длины дуги кривой .

Решение. Представим уравнение кривой в виде : (знаки в выражении у указывают, что кривая симметрична оси Ох).

Найдем производную функции :

,

тогда дифференциал длины дуги данной кривой

Следовательно,

Пример. Найти дифференциал длины дуги кривой .

Решение. Найдем производную функции :

,

тогда дифференциал длины дуги данной кривой

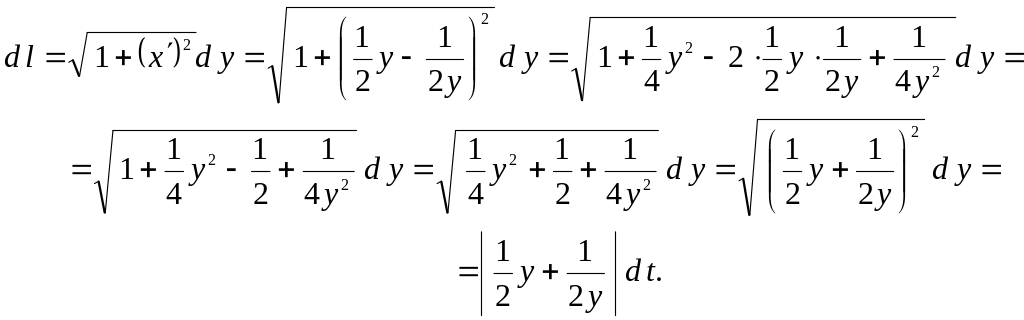
Следовательно,

Пример. Найти дифференциал длины дуги астроиды .

Решение. Дифференцируя по t, получим

,

.

тогда дифференциал длины дуги астроиды

Следовательно,

Пример. Найти дифференциал длины дуги логарифмической спирали .

Решение. Найдем производную функции :

,

тогда дифференциал длины дуги логарифмической спирали

Следовательно,

Упражнения.

Найти дифференциал длины дуги следующих кривых:

1. ;	2. ;
3. ;	4. ;
5.	6.

2.18.Кривизна

Первая производная функции f (x) характеризует направление линии , а вторая производная устанавливает меру её изогнутости, или искривленности.

Определение. Углом смежности дуги линии называется угол между касательными в ее конечных точках, а отношение угла смежности дуги к ее длине называется средней кривизной дуги _ср .

Определение. Кривизной k линии в некоторой ее точке называет­ся предел, к которому стремится средняя кривизна _ср дуги линии при стремлении конечной точки дуги к ее начальной точке, т. е.

.

В частности, кривизна окружности радиуса r есть _окр = , кривизна прямой равна нулю.

Если плоская кривая отнесена к прямоугольной системе координат и задана уравнением , то кривизна k дуги выражается формулой

.

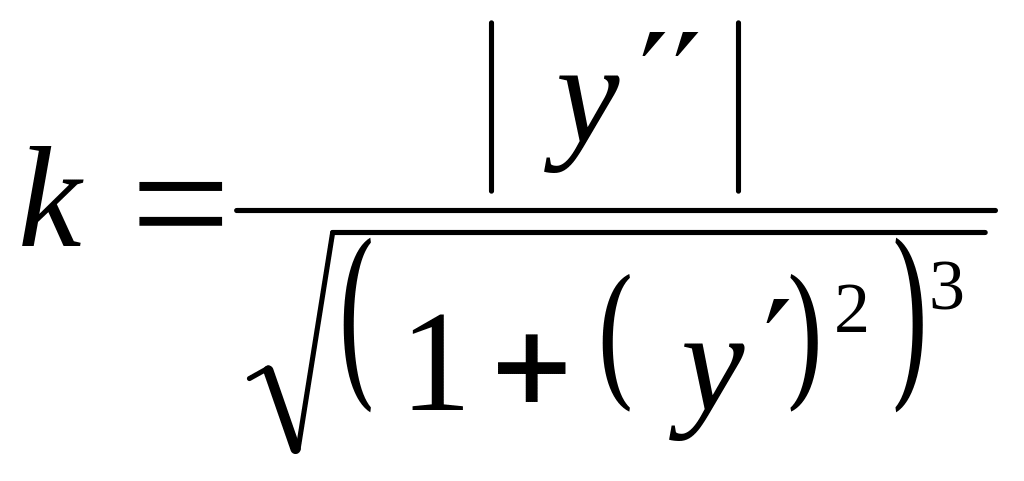Eсли плоская кривая отнесена к прямоугольной системе координат и задана параметрически системой уравнений , то кривизна k дуги выражается формулой

,

где , , , .

Если плоская кривая отнесена к полярной системе координат и задана уравнением , то кривизна k дуги выражается формулой

,

где , .

Пример. Найти кривизну линии в точке с абсциссой .

Решение. Найдем значения производных первого и второго порядков функции в точке с абсциссой :

,

.

Подставим найденные значения и в формулу

:

Следовательно, кривизна линии в точке с абсциссой

Пример. Найти кривизну циклоиды в точке .

Решение. Дифференцируя по t, получим

, .

Вычислим значения производных в точке :

, .

Подставляя найденные значения , в формулу

,

имеем

.

Следовательно, кривизна циклоиды в точке

.

Пример. Найти кривизну кардиоиды в точке .

Решение. Найдем значение функции в точке с абсциссой :

Найдем значения производных первого и второго порядков функции в точке с абсциссой :

Подставим значения в формулу :

.

Следовательно, кривизна кардиоиды в точке

.

Упражнения.

Найти кривизну дуги в заданной точке следующих линий:

1. , .	2. , .
3. , .	4. , .