
- •Дифференциальное исчисление функций одной переменной в упражнениях и задачах.
- •Глава 1. Введение в анализ
- •Определение функции
- •Предел функции
- •1.3. Непрерывность функций
- •Глава 2. Дифференциальное исчисление функции одной переменной
- •2. 1. Задачи, приводящие к понятию производной
- •2.2. Определение производной
- •2.3. Дифференцирование функций
- •2.4. Приложения производной к задачам геометрии и механики.
- •2.5. Производные высших порядков
- •Применение второй производной в задачах механики
- •Дифференциал функции
- •2.8.Основные теоремы о дифференцируемых функциях
- •2.9.Раскрытие неопределенностей. Правило Лопиталя
- •2.9. Исследование функций с помощью производных
- •2.10. Локальный экстремум функции
- •2.11.Наибольшее и наименьшее значения функции
- •2.12. Выпуклость кривой. Точки перегиба
- •2.13. Асимптоты графика функции
- •2.14. Общая схема исследования функции
- •2.15. Формула Тейлора
- •2.16.Векторная функция скалярного аргумента
- •2.17.Дифференциал длины дуги
- •2.18.Кривизна
- •Радиус, центр и круг кривизны. Эволюта и эвольвента
- •Литература
- •Содержание
- •Глава 1. Введение в анализ………………………………………3
- •1.1. Определение функции………………………………………………….3
- •Глава 2. Дифференциальное исчисление функции одной переменной………………………………………………………..28
2.11.Наибольшее и наименьшее значения функции
Пусть
у
= f
( x
) непрерывна
на отрезке [а,
b].
По
свойству функций, непрерывных на
отрезке, найдется такая точка
![]() ,
что
,
что
![]()
Тогда
либо х0
= а,
либо х0
= b,
либо
.
В
последнем случае точка
является критической точкой. Предположим,
что критических точек у функции
f
( x
) на
[а,
b]
имеется
лишь конечное число
![]() .
Тогда
.
Тогда
![]() .
.
Аналогично,
![]() .
.
Наибольшее
(наименьшее) значение непрерывной
функции
![]() на отрезке [а,
b]
достигается или в критической точке,
или нам концах отрезка. Для определения
наибольшего (наименьшего) значения
функции надо вычислить значения во всех
критических точках на
отрезке [а,
b],
значения
на отрезке [а,
b]
достигается или в критической точке,
или нам концах отрезка. Для определения
наибольшего (наименьшего) значения
функции надо вычислить значения во всех
критических точках на
отрезке [а,
b],
значения
![]() ,
,
![]() функции на концах отрезка и выбрать
наибольшее (наименьшее) из полученных
чисел.
функции на концах отрезка и выбрать
наибольшее (наименьшее) из полученных
чисел.
При нахождении наибольшего и наименьшего значений непрерывных функций используется свойство:
Если в некотором интервале (конечном или бесконечном) функция непрерывна и имеет только одну точку экстремума и если это точка максимума (минимума), то в ней функция принимает наибольшее (наименьшее) значение в этом интервале.
Пример.
Найти наибольшее и наименьшее значения
функции
![]() на отрезке [-2; 3].
на отрезке [-2; 3].
Решение.
Найдем производную функции
![]() и приравняем её к нулю для нахождения
критических (стационарных) точек:
и приравняем её к нулю для нахождения
критических (стационарных) точек:
![]() .
.
Так
как
![]() ,
а
,
а
![]() ,
то найдем значение производной в
критической точке
,
то найдем значение производной в
критической точке
![]() и на концах отрезка:
и на концах отрезка:
![]() ;
;
![]() ;
;
![]() .
.
Следовательно,
![]() ,
,
![]() .
.
Пример.
Найти наибольшее и наименьшее значения
функции
![]() на отрезке [1; e].
на отрезке [1; e].
Решение. Найдем производную функции
![]()
и приравняем её к нулю для нахождения критических точек:
![]()
![]()
![]() .
.
Так
как ни одна из критических точек не
принадлежит заданному отрезку[1; e],
то наибольшее и наименьшее значения
функции
находятся на концах отрезка. Вычислим
![]() и
и
![]() :
:
![]() ,
,
![]() .
.
Следовательно,
![]() ,
,
![]() .
.
Пример.
Найти
наибольшее и наименьшее значения функции
![]() на промежутке
на промежутке
![]() .
.
Решение. Используя формулу тригонометрии,
![]() ,
,
представим функцию в виде
![]() .
.
Из
записи функции видно, что функция чётная
и имеет период
![]() .
.
Следовательно,
наибольшее и наименьшее значения функции
достаточно искать среди экстремумов
функции на отрезке
![]() .
.
Найдем
производную
![]() :
:
![]() .
.
На отрезке производная обращается в нуль в точках
![]() .
.
Найдем значения функции в этих точках:
![]() ;
;
![]()
![]()
![]() ;
;

![]()
![]() ;
;
![]() .
.
Следовательно,
![]() ,
,
![]() .
.
Пример. Число 100 записать в виде произведения двух положительных чисел, сумма которых наименьшая.
Решение.
Пусть х
– первый множитель, тогда
![]() – второй множитель. Сумма этих чисел
х
+
– второй множитель. Сумма этих чисел
х
+
![]() .
По условию задачи х
>
0. Таким образом, задача свелась к
нахождению такого значения х,
при котором функция
.
По условию задачи х
>
0. Таким образом, задача свелась к
нахождению такого значения х,
при котором функция
![]() принимает наименьшее значение на
интервале
принимает наименьшее значение на
интервале
![]() .
.
Найдем производную функции
![]()
и приравняем её к нулю для нахождения критических точек:
![]()
![]()
![]() .
.
На
интервале
![]() имеется только одна стационарная точка
имеется только одна стационарная точка
![]() .
При переходе через точку
производная меняет знак с « – » на « +
», поэтому точка
является точкой минимума и в ней функция
.
При переходе через точку
производная меняет знак с « – » на « +
», поэтому точка
является точкой минимума и в ней функция
![]() принимает наименьшее значение (на
основании свойства непрерывной функции).
принимает наименьшее значение (на
основании свойства непрерывной функции).
![]() .
.
Таким
образом, 10 – первый множитель,
![]() – второй множитель.
– второй множитель.
Следовательно,
100 = 10![]() 10.
10.
Пример. Определить размеры открытого бассейна с квадратным дном объемом 32 м 2 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение.
Обозначим сторону основания через х,
а высоту через у.
Тогда объем бассейна будет равен
![]() ,
по условию задачи
,
по условию задачи
![]() .
.
Облицовываемая поверхность бассейна S состоит из поверхности стен и дна, т. е.
![]() .
.
Выразим
из соотношения
![]() величину у:
величину у:
![]() и подставим её в формулу
и подставим её в формулу
.
Получим функцию
![]() ,
,
определённую на промежутке .
Найдем производную функции
![]()
и приравняем её к нулю для нахождения критических (стационарных) точек:
![]() .
.
При
переходе через точку
![]() производная меняет знак с « – » на
« + », поэтому точка
является точкой минимума и в ней функция
производная меняет знак с « – » на
« + », поэтому точка
является точкой минимума и в ней функция
![]() принимает наименьшее значение (на
основании свойства непрерывной функции).
принимает наименьшее значение (на
основании свойства непрерывной функции).
Так как , то
![]() .
.
Следовательно,
искомые размеры бассейна
и
![]() ,
при которых на облицовку стен и дна
пошло наименьшее количество материала.
,
при которых на облицовку стен и дна
пошло наименьшее количество материала.
Пример. Сила действия кругового электрического тока на небольшой магнит, ось которого расположена на перпендикуляре к плоскости круга, проходящем через центр, выражается формулой
 ,
,
где
а
– радиус круга; х
– расстояние от центра круга до магнита
![]() ;
С
– постоянная величина. При каком
значении х
величина
F
будет
наибольшей?
;
С
– постоянная величина. При каком
значении х
величина
F
будет
наибольшей?
Решение. Найдем производную функции

и приравняем её к нулю для нахождения критических (стационарных) точек:
![]() .
.
Так
как
![]() ,
то функция
,
то функция

имеет
единственную стационарную точку
![]() .
.
При
переходе через точку
производная меняет знак с « + » на «– »,
поэтому точка
является точкой максимума и в ней функция
 принимает наибольшее значение (на
основании свойства непрерывной функции).
принимает наибольшее значение (на
основании свойства непрерывной функции).
Следовательно, при величина F будет наибольшей.
Упражнения
Найти наибольшее и наименьшее значения функции
 на отрезке [0; 4].
на отрезке [0; 4].Найти наибольшее и наименьшее значения функции
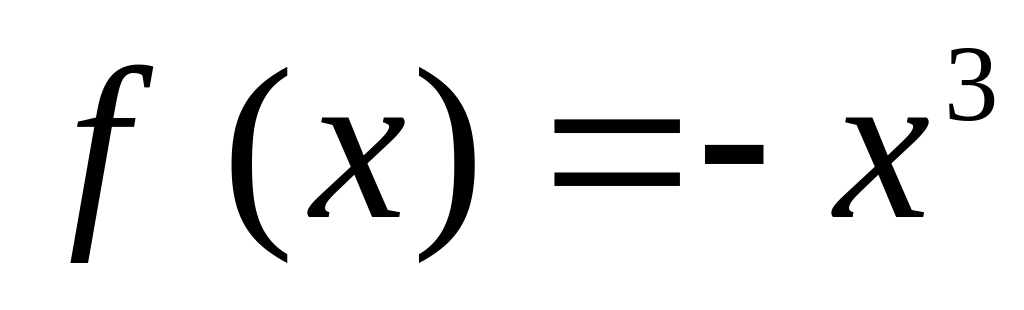 на отрезке [-2; 2].
на отрезке [-2; 2].Найти наибольшее и наименьшее значения функции
 на промежутке
.
на промежутке
.
Найти наибольшее и наименьшее значения функции
 на промежутке
.
на промежутке
.
Найти наибольший объем конуса, образующая которого l.
Найти наибольший объем цилиндра при данной боковой поверхности S.
На прямой между двумя источниками света силы F и 8F найти наименее освещенную точку, если расстояние между источниками 24 м. (Освещенность точки обратно пропорциональна расстоянию от источника света.)
Если источником тока служит элемент, то эффект Р (вт), получающийся при включении в цепь сопротивления W (ом), выражается формулой
 ,
где E
(в) – электродвижущая сила,
,
где E
(в) – электродвижущая сила,
 (ом)
–– внутреннее сопротивление. Найти
наибольший эффект, который можно
получить при данных Е
и
.
(ом)
–– внутреннее сопротивление. Найти
наибольший эффект, который можно
получить при данных Е
и
.
