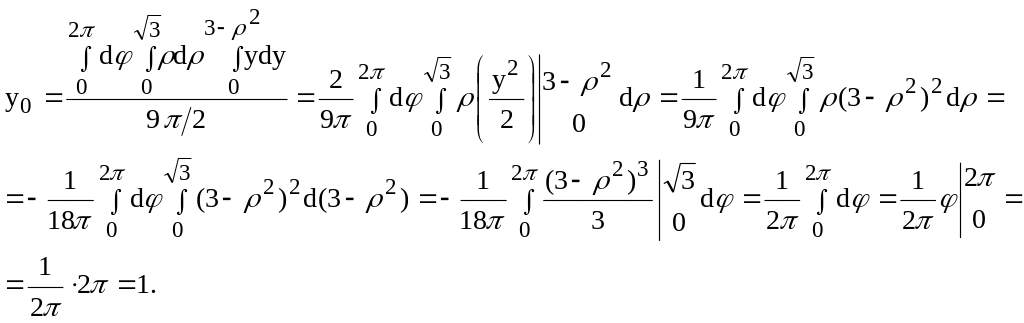3. Приложения тройного интеграла.

А. Вычисление объемов.

О

( 12)

бъем пространственного тела Т находится по формуле:

(см. первое свойство тройного интеграла)

В цилиндрических и сферических координатах соответственно имеем:

( 13) ( 14)

Пример 7.

Вычислить объем тела, ограниченного поверхностями: z = x² + y², x = 0, y = 0, z = 1, z = 2 и расположенного в первом октанте.

Для вычисления тройного интеграла, задающего объем данного тела, воспользуемся цилиндрическими координатами:

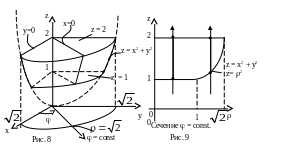
Отметим, что z = x² + y² – параболоид вращения, сечение которого плоскостями z = const – окружности, имеющие радиус . Поэтому данное тело имеет указанный на рис. 8 вид. Для точек тела угол  меняется в пределах от 0 до /2. При каждом фиксированном   меняется от 0 до – радиуса верхнего основания тела (рис. 9). Так как нижняя граница изменения z задается по-разному на разных участках: при 0 <  < 1, 1< z < 2, а при 1 <  < , x² + y² = ² < z < 2 то интеграл разобьется на два:

Пример 8.

Вычислить объем тела, ограниченного цилиндрами z = 4-y² и z = y² + 2 и плоскостями x = -1, x = 2.

Т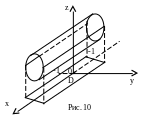 ело, объем которого находим (рис. 10), ограничено снизу цилиндром z = y² + 2, а сверху – цилиндром z = 4-y².

Оно проектируется в область D плоскости xOy, ограниченную прямыми x = -1, x = 2, y = 1 и y = -1.

1

Два последних уравнения получены в результате исключения z из уравнений цилиндров.

С учетом симметрии области V относительно плоскости xOz, имеем:

2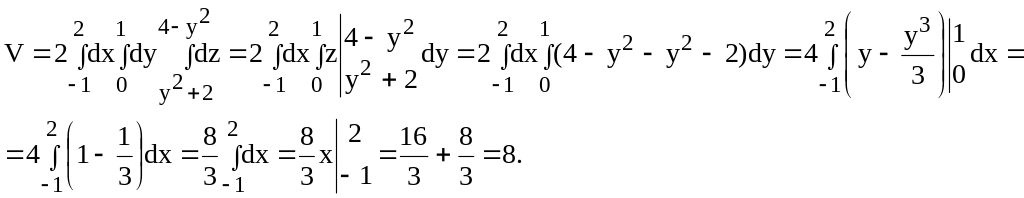

Пример 9.

В

Объем искомого тела (рис. 11) ограничен «снизу» конусом x² = y² + z², а «сверху» – параболоидом x = 6-y²–z² и проектируется в область D плоскости yOz, ограниченную окружностью y² + z² = 4. Последнее уравнение получено в результате исключения х из уравнений конуса и пара болоида. Введем цилиндричес-кие координаты:

ычислить объем тела, ограниченного параболоидом x = 6-z²-y² и конусом x² = y² + z² (x > 0).

y = cos, z = sin, x = x.

С учетом того, что данное тело симметрично относительно плоскостей xOz и xOy и что уравнения окружности, ограничивающей область D, конуса и параболоида, соответственно, принимают вид  = 2, x =  и х = 6-², имеем:

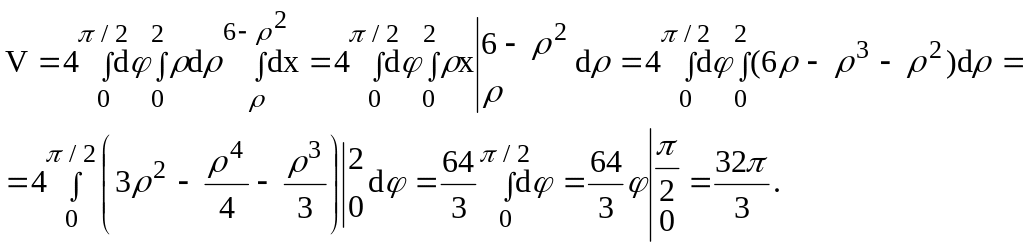
В. Приложения к механике.

Приложения тройных интегралов к механике проистекают из задач, связанных с непрерывным распределением массы в пространственной области.

Пусть Т – область пространства, занимаемая каким-либо материальным телом с плотностью (x, y, z). Тогда

а) ( 15)

где m – масса этого тела;

б) моменты инерции I_x, I_y, I_z относительно координатных осей Ox, Oy, Oz; I_xy, I_xz, I_yz относительно координатных плоскостей xOy, xOz, yOz; I₀ относительно начала координат, соответственно, определяются по формулам:

( 16)

( 17)

( 18)

в) координаты центра тяжести тела находятся по формулам:

( 19)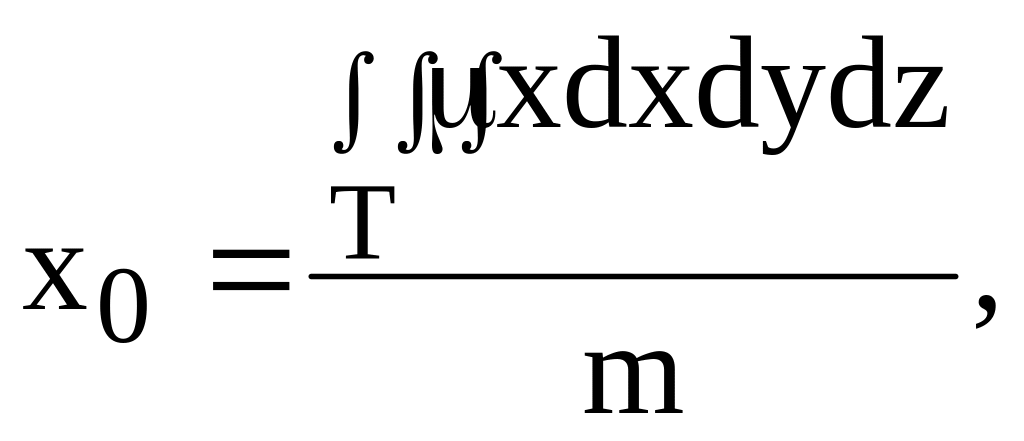

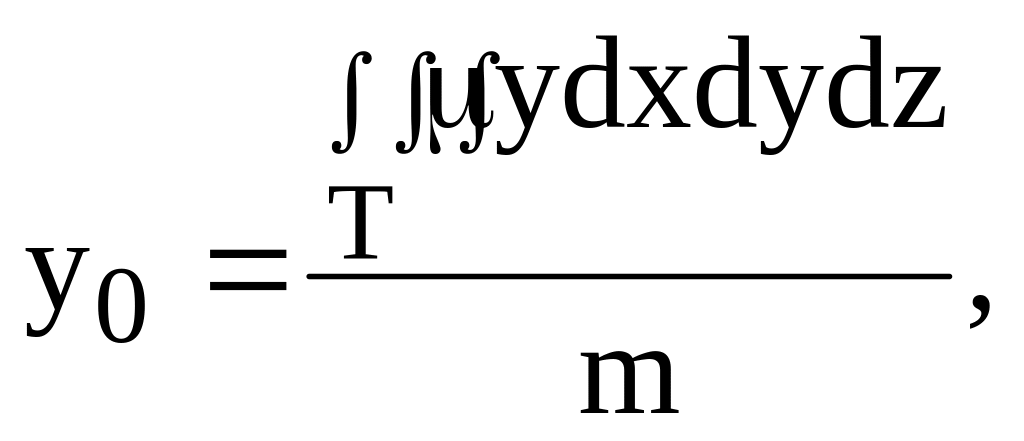
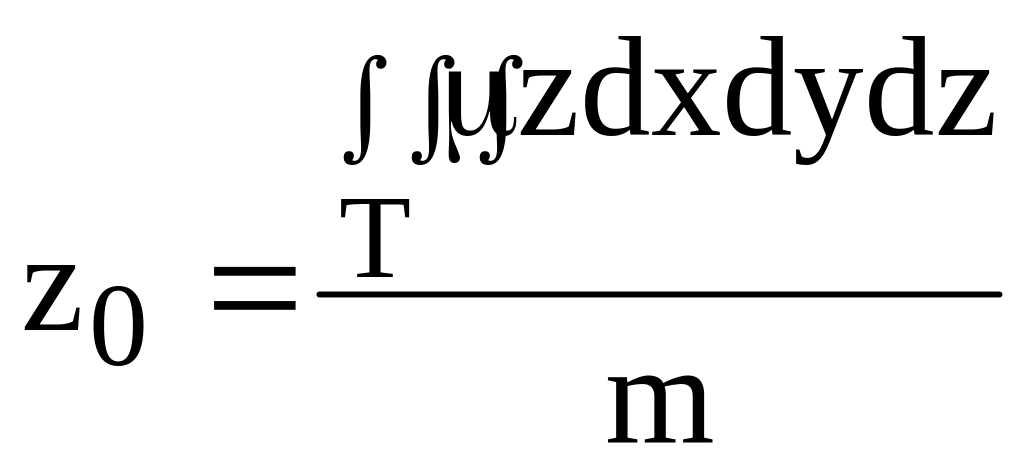
Для однородного тела ( = const) эти формулы упрощаются, т.к. в этом случае можно считать, что  = 1.

Пример 10.

Найти массу и момент инерции относительно оси Oz однородного тела Т, ограниченного поверхностями: z = 4-x²-y² и 4-2z = x² + y².

Тройной интеграл, как было указано выше, позволяет вычислить обе указанные характеристики, если известна объемная плотность тела (x, y, z):

где h = h (x,y,z) – расстояние от текущей точки до оси, относительно которой вычисляется момент инерции, в нашем случае это ось Oz, т.е. h² = x² + y².

В случае однородного тела (x, y, z) = const = , и тогда:

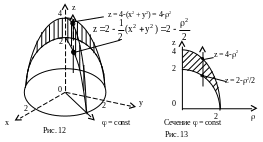
Для вычисления указанных тройных интегралов в данной задаче удобно воспользоваться цилиндрическими координатами. Уравнения данных поверхностей в цилиндрической системе имеют вид: z = 4-² и 4-2z = ². Решая их совместно, получим, что эти поверхности пересекаются по окружности x² + y² = 4, z = 0, или в цилиндрической системе координат:  = 2, z = 0.

Итак, данное тело ограничено двумя параболоидами вращения, которые пересекаются по окружности радиуса 2, лежащей в плоскости Oxy (рис. 12).

Ясно, что  меняется от 0 до 2. При каждом фиксированном  величина  меняется от 0 до 2, а при фиксированных  и  величина z меняется от 2-1/2² до 4-² (см. рис. 13). Таким образом, имеем:

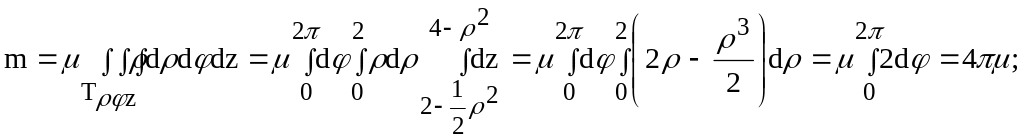
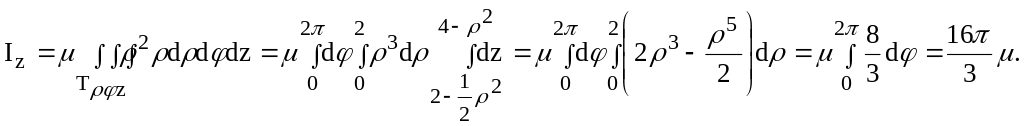
Ответ: m = 4(кг); (кгм²).

Пример 11.

Н айти расположение центра масс однородного полушара Т. Выберем прямоугольную систему координат с началом в центре шара так, как указано на рис. 14. Ясно, что абсцисса и ордината центра масс x_c = y_c = 0.

Для нахождения z_c воспользуемся известной формулой: В предпоследнем равенстве использована однородность тела, а в последнем – определение объемной плотности однородного тела. Хотя объем тела v можно вычислить с помощью тройного интеграла, но в нашем случае имеется «школьная» формула V Оставшийся тройной интеграл вычислим в сферических координатах:

Так как в рассматриваемом случае 0 <  < 2, 0 <  < /2, 0 < r < R, то

Ответ: x_c = y_c = 0, z_c = (8/3)R.

Пример 12. (см. пример 2 стр. 183)

Найти массу тела с плотностью  = x + y + z, ограниченного плоскостями x = 0, x = 1, y = 0, y = 1, z = 0, z = 1.

Тело, массу которого необходимо найти, является прямоугольным параллелепипедом. Согласно формуле ( 15) имеем:

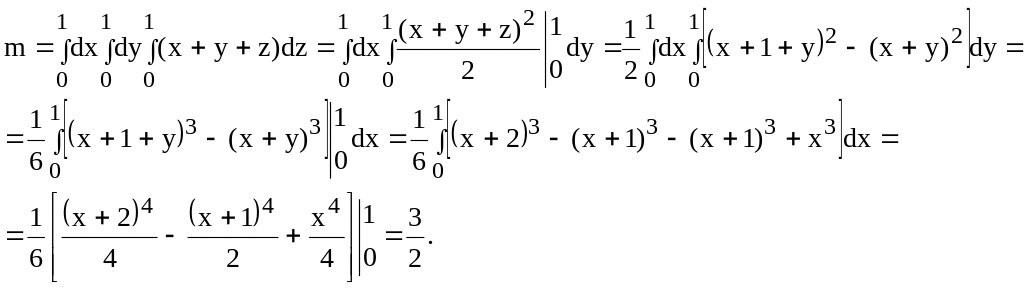
Пример 13.

Найти моменты инерции однородного ( = 1) цилиндра с высотой «h» и радиусом основания «а» относительно диаметра основания и относительно оси цилиндра, считая, что ось цилиндра направлена по оси Ох.

Поместим начало координат в центр нижнего основания цилиндра. Тогда уравнение цилиндра будет иметь вид y² + z² = a². Моменты инерции, которые мы находим, будут равны моментам инерции относительно координатных осей Oz и Ox. Следовательно, имеем:

Введем цилиндрические координаты: y = cos, z = sin, x = x, и тогда

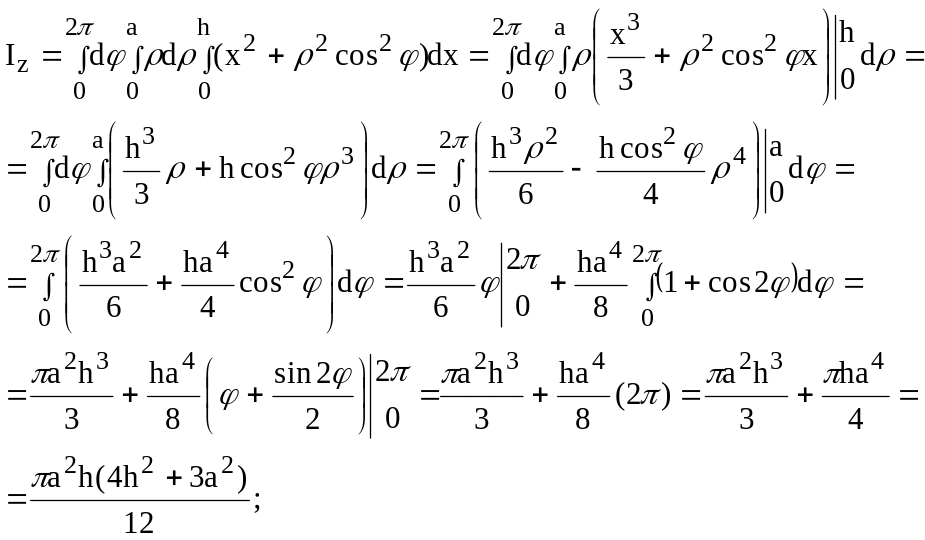
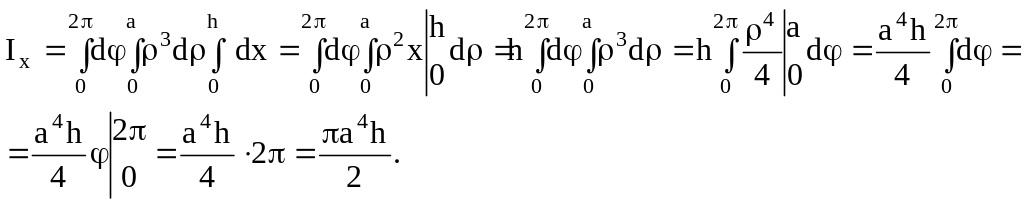
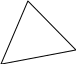
Пример 14.

О

z

пределить момент инерции однородной пирамиды ( = 1) относительно координатной плоскости xOy, если пирамида ограничена плоскостями x + y + z = 1, x = 0, y = 0, z = 0 (см. рис. 15). Согласно формулам ( 17) имеем:

1

z=1-x-y

y

0

0

y

1

x

1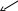

x

Рис. 15

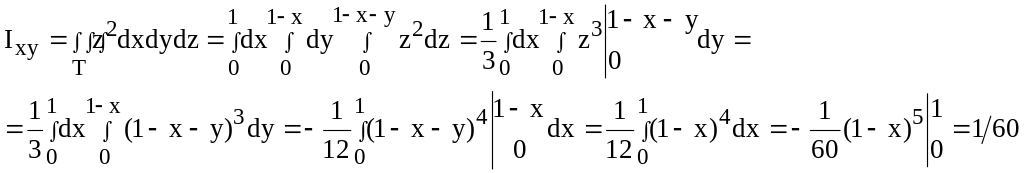
Пример 15.

Вычислить момент инерции однородного шара (=1) радиуса 1 относительно его центра. Поместим начало координат в центр шара. Тогда момент инерции шара относительно центра будет равен моменту инерции шара относительно начала координат. Согласно формуле (18) имеем:

Введя сферические координаты, получим:

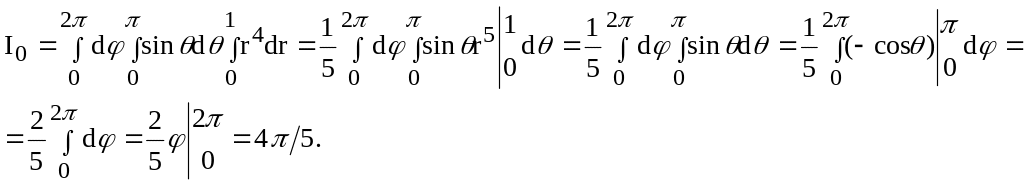
Пример 16.

Найти координаты центра тяжести однородного тела, ограниченного параболоидом и плоскостью у = 0 (у 0).

В силу симметрии тела относительно координатных плоскостей уОz и хОу (см. рис. 22 §1) x₀ = z₀ = 0. Для нахождения y₀ найдем массу тела m. Введем цилиндрические координаты:

Согласно формулам (15), ( 19) имеем: