1. Построение. Вычисление тройных интегралов в декартовых прямоугольных координатах.

Тройной интеграл представляет собой одно из возможных обобщений двойного интеграла на случай функции трех переменных.

Пусть в пространственной области Т задана функция f(x, y, z). Проделаем 5 операций:

6. Разобьем область Т на n частей Т₁, Т₂,…,Т_n, не имеющих между собой общих внутренних точек. Обозначим объемы и диаметры этих частей соответственно черезv₁, v₂,…, v_n и ₁, ₂, …, _n. Наибольший из диаметров обозначим через  и назовем его рангом дробления.

7. Выберем в каждой частичной области Т_k(k = 1, 2, …, n) по точке (x_k; y_k; z_k) и вычислим в ней значение функции f(x, y, z), т.е. найдем числа f(x_k, y_k, z_k).

8. Вычислим произведения f(x_k, y_k, z_k)v_k.

9. Найдем сумму которую называют интегральной суммой для функции f(x, y, z) в области Т, отвечающей выбранному дроблению на частичные области и выбору точек (x_k, y_k, z_k).

10. Измельчая дробление, ищем предел

( 1)

Е

( 2)

сли существует конечный предел (1), не зависящий ни от способа дробления области Т на части, ни от выбора точек (x₁, y₁, z₁), (x₂, y₂, z₂),…, (x_n, y_n, z_n), то этот предел называют тройным интегралом от функции f(x, y, z) по области Т и обозначают символами:

При этом функцию f(x, y, z) называют подынтегральной функцией, Т – областью интегрирования, x, y, z – переменными интегрирования, а dv (или dxdydz) – элементом объема.

Т

( 3)

аким образом, имеем по определению:

Приведем простейшие свойства тройного интеграла, которые непосредственно следуют из определения его и доказываются аналогично соответствующим свойствам определенного и двойного интегралов.

1. Если в области Т f(x, y, z)  1, то где V =V_Т – объем области Т.

2. Постоянный множитель К в подынтегральной функции можно выносить за знак тройного интеграла:

3. Тройной интеграл от суммы двух функций равен сумме тройных интегралов от слагаемых:

Свойства 2 и 3 выражают свойство линейности тройного интеграла относительно подынтегральной функции.

4. Если область интегрирования Т разбита на две части Т₁ и Т₂, то

Это свойство называют свойством аддитивности тройного интеграла относительно области интегрирования.

5. Если всюду в области Т функция f(x, y, z) удовлетворяет условию f(x, y, z) > 0, то

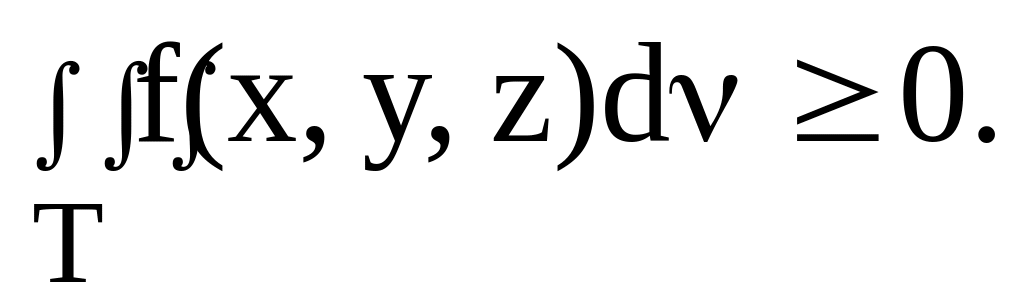
6. Если всюду в области Т функции f(x, y, z) и (x, y, z) удовлетворяют условию f(x, y, z) > (x, y, z), то

7. Имеет место неравенство:

8. (Теорема о среднем.) Если функция f(x, y, z) непрерывна в замкнутой области Т, то в этой области найдется хотя бы одна такая точка , что будет иметь место равенство:

V_Т,

где V_Т – объем области Т.

Вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

Осуществляется это с помощью следующих теорем.

Теорема 1

Если _ху – замкнутая плоская область, являющаяся проекцией на плоскость Oxy замкнутой пространственной области Т, поверхность которой снизу и сверху описывается уравнениями z = h(x,y) и z = H(x,y), где h(x,y) и H(x,y) – непрерывные функции в _x,y, и цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей является граница области _x,y (рис. 1), то для любой функции f(x,y,z), непрерывной в Т, имеет место формула

( 4)

(4)

Если при этом область _x,y ограничена линиями x = a, x = b, y = (x), y = (x), где a < b, а функции (x) и (x) непрерывны на промежутке [a, b] и удовлетворяют условию (x) < (x), то, переходя в формуле ( 4) от двойного интеграла к повторному, получим формулу:

( 5)

(5)

При вычислении тройного интеграла по формуле (5) сначала вычисляется внутренний интеграл по переменной z при постоянных x и y, затем полученная функция от х и y интегрируется по переменной y при постоянном х, а затем полученная функция от х интегрируется по х в пределах от а до b.

Если область Т спроектировать не на плоскость Oxy (как в теореме 1), а на Oyz, то получим следующий аналогичный результат.

Теорема 2

Если _yz – замкнутая плоская область, являющаяся проекцией на плоскость Oyz замкнутой пространственной области Т, поверхность которой сзади и спереди описывается уравнениями x = h(y,z) и x = H(y,z), где h(y,z) и H(y,z) – непрерывные функции в _yz, и цилиндрической поверхностью, у которой образующая параллельна оси Oх, а направляющей является граница области _yz, то для любой функции f(x,y,z), непрерывной в Т, имеет место формула:

( 6)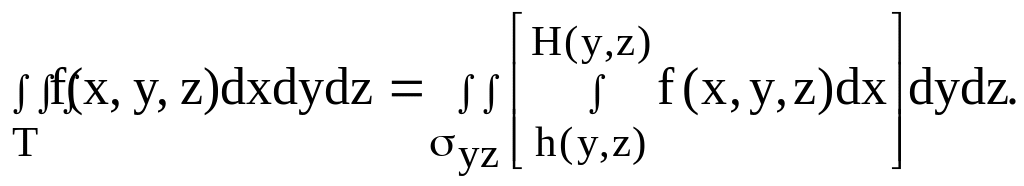

Если при этом область _yz ограничена линиями y = с, y = d, z = (у), z = (у), где c < d, а функции (y) и (y) непрерывны на промежутке [c, d] и удовлетворяют условию (x) < (x), то, переходя в формуле ( 6) от двойного интеграла к повторному, получим формулу:

( 7)

При вычислении тройного интеграла по формуле (7) сначала вычисляется внутренний интеграл по переменной x при постоянных y и z, затем полученная функция от y и z интегрируется по переменной z при постоянном y, а затем полученная функция от y интегрируется по y в пределах от c до d.

Если область T спроектировать на плоскость Oxz, то можно получить теорему 3, аналогичную теоремам 1 и 2.

Выражения, стоящие в правых частях равенств (5) и (7), называют повторными (трехкратными) интегралами.

Заметим, что пределы интегрирования будут постоянными во всех трех интегралах только в том случае, если областью интегрирования является параллелепипед с гранями, параллельными координатным осям.

Если область интегрирования T имеет более сложный вид, то ее следует разбить на конечное число частей, каждая из которых удовлетворяет условиям одной из указанных теорем. Интеграл по области при этом заменяется суммой интегралов по ее частям.

При вычислении тройных интегралов основную трудность обычно составляет (как, впрочем, и для двойных) расстановка пределов интегрирования при переходе к повторным (трехкратным) интегралам.