Пример 16.

Вычислить двойной интеграл если область D ограничена эллипсом

Для решения этой задачи удобно ввести так называемые обобщенные полярные координаты, положив y = acos, z = bsin.

Найдем якобиан данного преобразования:

т.е. | I |= ab.

Подынтегральная функция принимает вид:

Теперь имеем:

Угол  меняется от 0 до 2. Уравнение эллипса принимает вид  = 1, поэтому  меняется от 0 до 1. И тогда

4. Приложения двойного интеграла

А. Вычисление площадей плоских областей.

Площадь S плоской области D на плоскости xOy вычисляется по формуле (см. первое свойство двойного интеграла)

.

Пример 17.

Вычислить площадь плоской области D, ограниченной прямой y = 2 и параболой y = x² - 1.

Область D (рис. 18) можно проектировать и на ось Ох, и на ось Oy. Спроектируем ее на ось Oy. Область D симметрична относительно оси Oy, поэтому достаточно вычислить площадь правой половины области D и результат удвоить.

y

2

П равая половина области D проектируется на ось Oy в отрезок [-1; 2] и имеет левой границей прямую х = 0, а правой – линию y = x² –1, или .

В результате

откуда .

Пример 18.

В

φ= π/4

ычислить площадь плоской области D (рис. 19), ограниченной прямыми z = 0, z = x и окружностью x² + z² = 2x.

В

Рис. 19

ведем полярные координаты x = cos, z = sin. Уравнение окружности, ограничивающей область D, примет вид ² = 2cos, или  = 2cos.

Угол  меняется от 0 до /4, а  меняется от 0 до 2cos. Тогда получаем:

Пример 19.

(х² + z²) ² = 2ax³.

Введем полярные координаты: x = cos, z = sin. Уравнение кривой примет вид ⁴ = 2a³cos³, или  = 2acos³.

Область D (рис.20) симметрична относительно оси Ox, поэтому достаточно вычислить площадь верхней половины области D и результат удвоить. Для верхней половины области D угол  меняется от 0 до /2, а  меняется от 0 до 2acos³.

z

0 2a x

Рис. 20

Поэтому имеем:

откуда S = 5a²/8.

В. Вычисление объемов.

Объем цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), а снизу – областью D плоскости xOy (рис. 21), находится по формуле (см. геометрический смысл двойного интеграла):

( 16)

.

Если тело не является цилиндрическим, то его разбивают на цилиндрические части.

Пример 20.

В ычислить объем тела, ограниченного плоскостями z = 0, y + z = 2 и цилиндром y = x².

Данное тело (рис. 21) сверху ограничено плоскостью z = 2 – y, поэтому

Область D есть параболический сегмент, ограниченный в плоскости xOy прямой y = 2 и параболой y = x². Спроектируем область D на ось Oy. Тогда, с учетом симметрии тела относительно плоскости yOz, получим:

откуда

Пример 21.

Вычислить объем тела, ограниченного плоскостью y = 0 и параболоидом y = 3 – x² – z².

В этой задаче удобно считать, что тело «стоит» на плоскости xOz и «сверху» (рис. 22) ограничено параболоидом y = 3 – x² – z², поэтому

z

Область D есть круг. Его границу x² + z² = 3 получим подстановкой y = 0 в уравнение y = 3 – x² – z². В полярных координатах уравнение этой окружности имеет вид ² = 3, или  = .

Учитывая симметрию тела относительно плоскостей xOy и yOz, найдем:

О

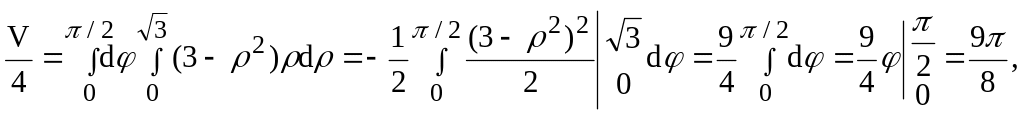
откуда

Пример 22.

Вычислить объем тела, вырезанного цилиндром x² + y² = Rx из сферы x² +y² + z² = R².

Н а рис. 23 изображена половина тела, объем которого мы и найдем (вторая половина, расположенная симметрично с первой, находится под плоскостью xOy).

Сверху тело ограничено сферой, уравнение которой x² + y² + z² = R², поэтому

Область D есть круг, ограниченный окружностью x² + y² = Rх. С учетом того, что половина тела симметрична относительно плоскости xOz и что уравнение окружности, ограничивающей область D, в полярных координатах имеет вид ² = Rcos, или  = Rcos, получаем:

Рис. 23

D

откуда

Пример 23.

Н айти объем тела, ограниченного поверхностями: x² + y² = 9 – z, y = x, x = 2, y = 0 , z=0.

Рис. 24

Заданное тело является цилиндроидом, так как это – часть некоторого цилиндра, ограниченная снизу плоскостью z = 0, а сверху – поверхностью z = 9 - x² - y² (рис. 24). Объем цилиндроида, ограниченного сверху поверхностью z = f(x, y), можно вычислить с помощью двойного интеграла по области, лежащей в его основании (рис. 1):

C. Вычисление площади поверхности

Пусть поверхность , заданная уравнением z = f(x, y), проектируется на плоскость xOy в область D (см. рис. 1). Тогда ее площадь S находят по формуле:

( 17)

Пример 24.

Н айти часть поверхности параболоида вращения z = x² +y², вырезанной плоскостями x = 0, y = 0 и z = 2 (x  0, y  0).

Для вычисления площади части поверхности, заданной явным уравнением z = f(x, y), используем формулу ( 17):

где D – проекция рассматриваемой части поверхности на плоскость О_ху.

В данной задаче D есть четверть круга, изображенная на рис. 25,26. Так как по условию задачи z = x² +y², то z’_x = 2x, z’_y = 2y и 1 + (z’_x)² + (z’_y)² = 1 + 4(x² + y²).

Введя полярные координаты, получим:

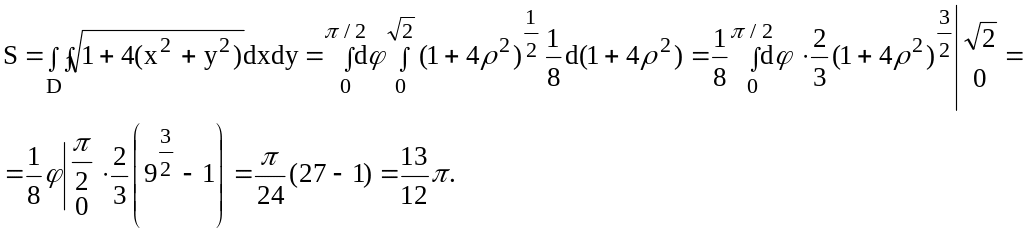
Пример 25.

В ычислить площадь части поверхности цилиндра z² = 4x, лежащей в I октанте, вырезанной цилиндром y² = 4x и плоскостью x = 1.

Из урав нения поверхности z² = 4x для первого октанта имеем:

и

Область D (рис. 27) есть параболический сегмент, ограниченный в плоскости xOy параболой y² = 4x, или и прямой x = 1. Тогда

у₂

х=1

0 1 х