IV. В Криволинейные и поверхностные интегралы.

Некоторые сведения из теории. Типовые задачи.

Криволинейные интегралы, как и кратные, представляют собой обобщение (в различных направлениях) определенного интеграла.

1. Криволинейные интегралы первого рода (по длине дуги) – кипр.

Пусть в пространстве Oxyz задана непрерывная спрямляемая кривая АВ, в точках которой определена произвольная функция f(x, y, z). Проделаем 5 операций:

1. Разобьем кривую АВ на n частей точками М₁, М₂, ….М_n-1, следующими друг за другом в направлении от А к В (для определенности). Точку А обозначим через М₀, точку В через М_n. Длины дуг М_k-1 М_k (k = 1, 2,…, n) обозначим, соответственно, через 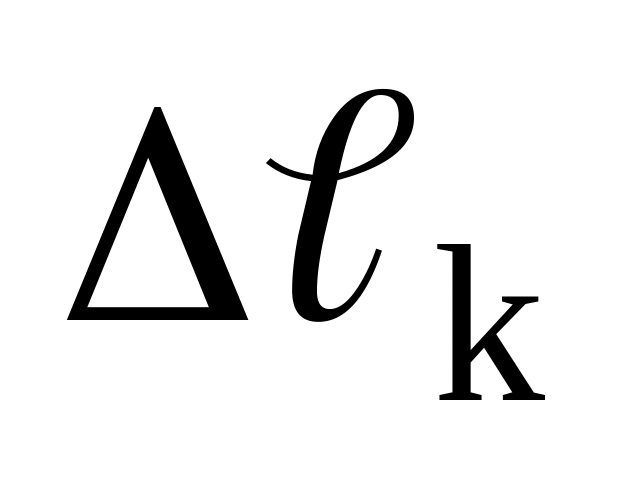. Наибольшую из величин (k = 1, …, n) обозначим через и назовем рангом (шагом) дробления кривой АВ.

2. На каждой дуге М_k-1 М_k (k = 1, 2, …, n) выберем произвольным образом по точке N_k(x_k; y_k; z_k) и вычислим в них значения функции f(x, y, z), т.е. найдем числа f(x_k, y_k, z_k).

3. Вычислим произведения f(x_k, y_k, z_k) (k = 1, 2, …, n).

4. Найдем сумму которую называют интегральной суммой для функции f(x, y, z) на кривой АВ, отвечающей данному разбиению (дроблению) АВ на части и выбору точек N_k (x_k; y_k; z_k).

5. Измельчая дробление, ищем предел

( 1)

Если существует конечный предел ( 1), не зависящий ни от способа дробления кривой АВ на части, ни от выбора точек N_k(x_k; y_k; z_k) (k = 1, 2, …, n), то этот предел называют криволинейным интегралом первого рода (по длине дуги) от функции f(x, y, z) по дуге АВ и обозначают символом:

При этом функцию f(x, y, z) называют подынтегральной функцией, кривую АВ – линией (кривой, контуром) интегрирования, точку А – начальной, а точку В – конечной точками интегрирования (тем самым устанавливается направление интегрирования).

Таким образом, по определению

( 2)

Перечислим простейшие свойства криволинейного интеграла первого рода (в основном аналогичные свойствам определенного интеграла):

1. Значение криволинейного интеграла первого рода не зависит от направления на кривой:

2. Постоянный множитель в подынтегральной функции можно выносить за знак криволинейного интеграла:

3. Криволинейный интеграл первого рода от суммы двух функций равен сумме интегралов от этих функций:

4. Если кривая АВ разбита точкой С на две части АС и СВ, то криволинейный интеграл по всей кривой АВ равен сумме интегралов по ее частям:

5. Если в каждой точке кривой АВ функции f(x, y, z) и (x, y, z) удовлетворяют неравенству f(x, y, z) < (x, y, z), то

6. Имеет место неравенство:

7. Если f(x, y, z) = 1 на кривой АВ, то где L – длина кривой АВ.

8. (Теорема о среднем). Если функция f(x, y, z) непрерывна на кривой АВ то на этой кривой найдется хотя бы одна такая точка , что будет иметь место равенство: где L – длина кривой АВ.

Вычисление криволинейных интегралов первого рода сводится к вычислению определенных интегралов.

П

( *)

усть кривая АВ задана параметрическими уравнениями

x = (t), y = (t), z = (t),  < t < ,

где (t), (t), (t) – непрерывно дифференцируемые функции параметра t, причем, точкам А и В отвечают, соответственно, значения параметра t =  и t = .

Установим на кривой АВ направление интегрирования от точки А к точке В.

Тогда формула для вычисления криволинейного интеграла первого рода для случая, когда функция f(x, y, z) непрерывна на кривой АВ, имеет вид:

( 3)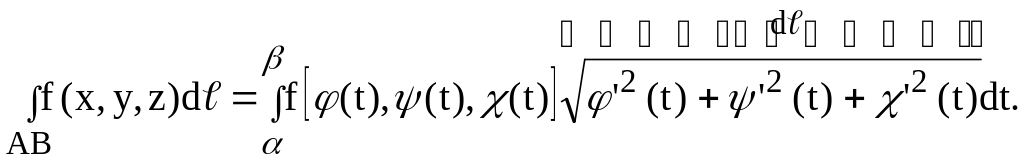

Таким образом, для вычисления криволинейного интеграла первого рода по кривой АВ следует: используя параметрические уравнения (*) кривой АВ, заменить у подынтегральной функции координаты x, y, z соответственно функциями (t), (t), (t); заменить d дифференциалом дуги как функции параметра t и проинтегрировать полученное выражение по t в пределах от  до .

Е

( **)

сли, в частности, кривая АВ – плоская и задана параметрическими уравнениями

x = (t), y = (t),  < t < ,

а

( 4)

функция f(x, y) непрерывна на АВ, то формула для вычисления криволинейного интеграла первого рода по кривой АВ имеет вид:

Е

( ***)

сли АВ – плоская кривая, заданная явно уравнением

y = f(x), a < x < b,

где f(x) – непрерывно дифференцируемая функция на [a, b] , то, принимая х за параметр, можно как частный случай формулы ( 4) получить формулу:

( 5)

Если кривая задана уравнением x = (y), где c < y < d, то

( 6)

Если кривая задана уравнением  = () (₁ <  < ₂), то , а

( 7)

Если различные участки контура интегрирования заданы различными уравнениями, то нужно разбить контур интегрирования на соответствующие части и весь интеграл вычислять как сумму интегралов, взятых по этим частям.

Пример 1.

Вычислить , где L – отрезок прямой, соединяющий точки О(0;0) и А(1;2).

Запишем уравнение прямой L: y = 2x (явное задание). Для данной линии При движении от О к А х меняется от 0 до 1. По формуле ( 5) имеем:

у = 2х

Пример 2.

Вычислить , где L – контур окружности y² + z² = ay (a > 0).

В ведем полярные координаты: y = cos, z = sin .

Уравнение окружности принимает вид: ² = acos или  = acos.

Тогда ’ = -asin и

Т. к. окружность расположена в той части плоскости yOz, где y > 0, то угол  меняется от -/2 до /2. По формуле ( 7) имеем:

Пример 3.

Вычислить , где L – дуга кривой, заданной параметрически: x = tcost, y = tsint, z = t (0 < t < 2).

Так как и по формуле ( 3) имеем:

Пример 4.

Вычислить , где L – дуга параболы y = x², 0 < x < 1.

Так как линия L задана явно, воспользуемся формулой ( 5):

Пример 5.

В

В случае, когда L – пространственная кривая, наиболее простой способ вычисления криволинейного интеграла I рода состоит в использовании параметрического задания кривой.

В этом случае вычислительная формула будет естественным обобщением аналогичной формулы для плоской кривой, т.е. это будет формула ( 3).

Параметрические уравнения линии L (рис. 1):

, z = Rsint, 0 < t < /2.

ычислить , если L – четверть пространственной окружности , лежащая в I октанте.

Поэтому

Пример 6.

Найти длину дуги линии x³ = 3a²y, 2xz = a², заключенной между плоскостями y = 9a, y = a/3.

Длину дуги L можно записать в виде : .

Приняв за параметр координату х, уравнения данной линии можно представить в параметрическом виде: x = t, y = t³/3a², z = a²/2t. Значения параметра, соответствующие концам рассматриваемой дуги, вычисляются по формуле: Таким образом, t₁ = a, t₂ = 3a.

Ответ: S = 9a.