3. Формула Грина и ее применение.

Важную роль в практических приложениях играет теорема, выражающая криволинейный интеграл через двойной по области , имеющей своим контуром линию L.

Т еорема Грина.

Если функции P(x, y) и Q(x, y) непрерывны вместе со своими частными производными Q/x и P/y в области , то имеет место формула:

( 20)

где L – граница замкнутой области , и интегрирование вдоль L производится в положительном направлении.

Формула Грина имеет место для любой области , ограниченной кусочно-гладким контуром L. Из (20) следует, что формулу Грина удобно применять для вычисления интегралов второго рода по замкнутому контуру.

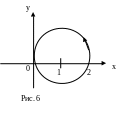
Пример 11.

Вычислить интеграл по окружности x² + y² = 2x, пробегаемой против часовой стрелки (рис. 6).

В рассматриваемой задаче . Обе функции непрерывны вместе со своими производными на всей плоскости, поэтому

где D – круг, ограниченный данной окружностью (x² – 1)² + y² = 1, т.е. круг радиуса 1 с центром в А(1;0). Вспоминая, что интеграл, стоящий в правой части, есть площадь области, получим: I = 3.

Пример12.

П рименяя формулу Грина, вычислить где – контур треугольника с вершинами в точках А(1;1), В(2;2) и С(1;3) (рис. 7).

В данном случае P = 2(x² + y²),

Применяя формулу Грина, получаем:

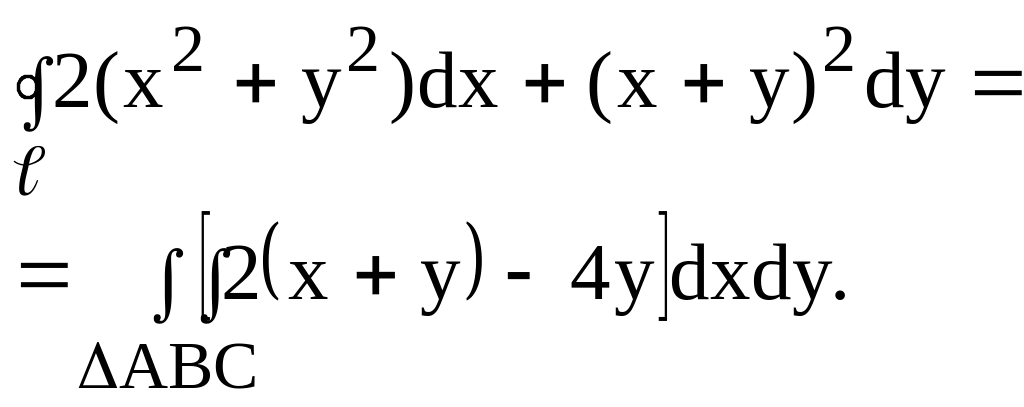
Вычисляя двойной интеграл, найдем (рис. 7):

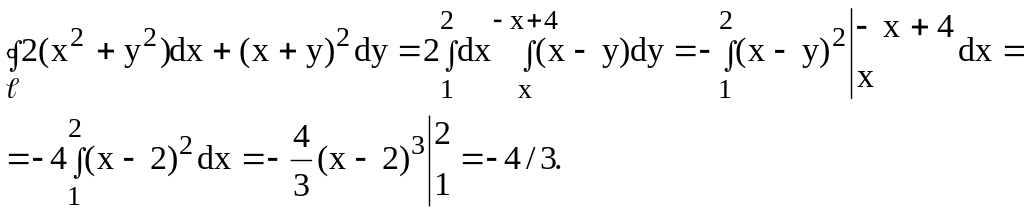
4. Условия независимости криволинейных интегралов от формы пути интегрирования ( условия нпи).

П

( 21)

усть функции P(x, y) и Q(x, y) непрерывны вместе со своими частными производными в односвязной и открытой области  плоскости Oxy. Рассмотрим криволинейный интеграл второго рода:

где А и В – произвольные точки из области , а АВ – произвольная кусочно-гладкая кривая, целиком лежащая в области . Может случиться, что интеграл ( 21) зависит лишь от координат точек А(x₀; y₀) и B(x₁; y₁), а от формы кривой АВ, целиком лежащей в , не зависит.

В этом случае его называют криволинейным интегралом, не зависящим от пути интегрирования (точнее, от формы этого пути) в области  и обозначают символом

или .

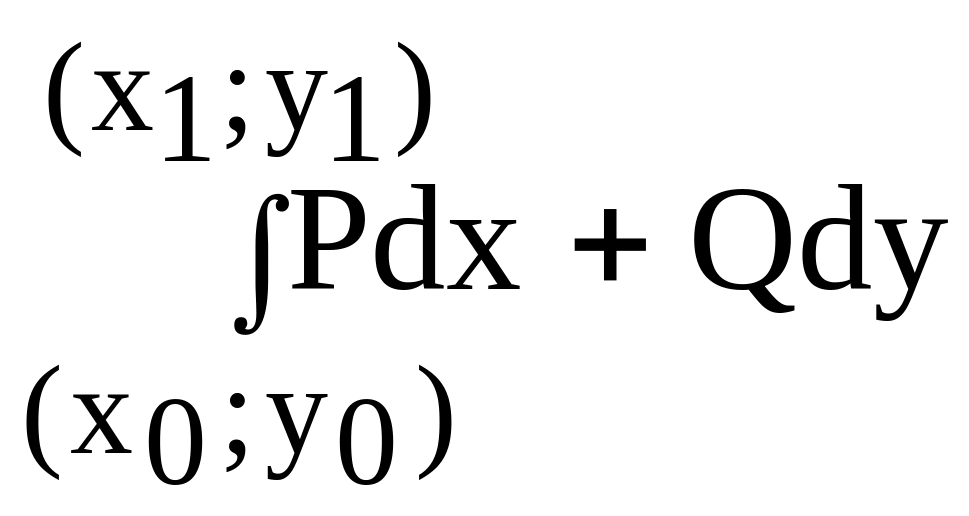Возникает вопрос: какие условия должны быть выполнены, чтобы интеграл ( 21) не зависел от пути интегрирования в области ?

Оказывается, что если функции P(x, y) и Q(x, y) определены и непрерывны вместе со своими частными производными Q/x и P/y в односвязной и открытой области , то следующие 4 утверждения равносильны:

1. Криволинейный интеграл 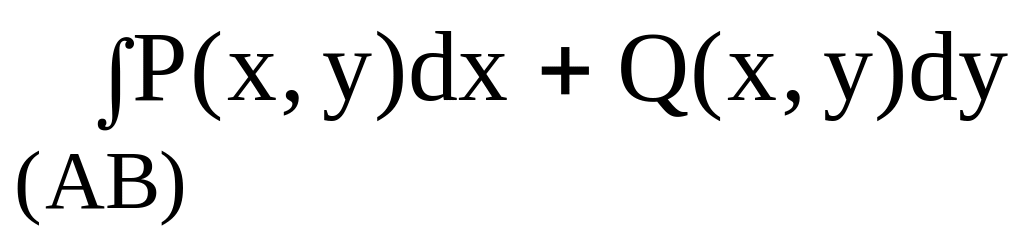зависит лишь от точек А и В, а от кривой АВ, целиком лежащей в области , не зависит.

2. Для любого замкнутого контура L, целиком лежащего в области ,

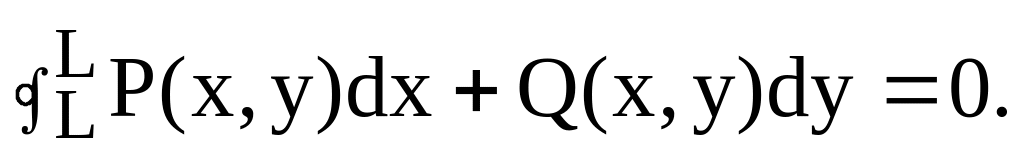
3. Всюду в области  выполняется тождество .

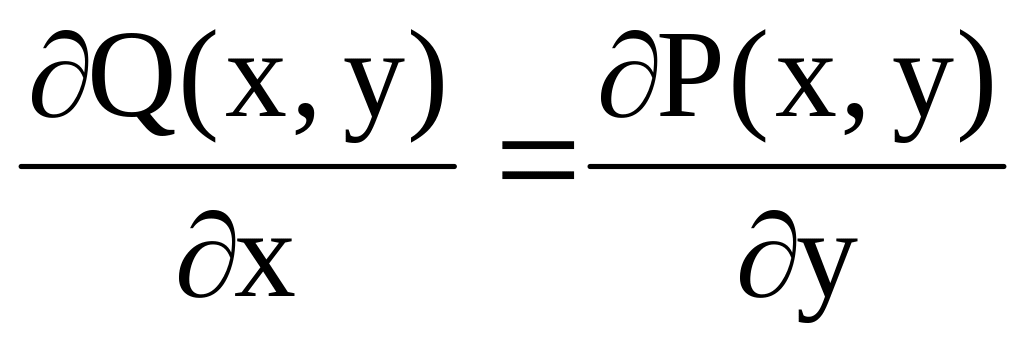4. Выражение P(x, y)dx + Q(x, y)dy является полным дифференциалом некоторой функции u(x, y) в области .

Если условия 1-4 выполняются, то криволинейный интеграл второго рода удобно вычислять по формуле:

( 21A)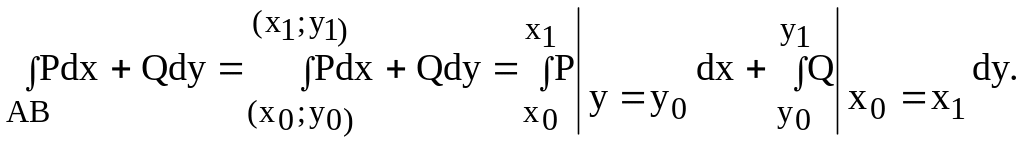

Эта формула получается, если за путь интегрирования взять ломаную АСВ, звенья которой параллельны осям координат (см. рис. 8). Формулу (21А) запоминать не надо: понимая ее суть, нужно в каждой конкретной задаче двигаться от начальной точки А к конечной точке В вдоль отрезков, параллельных осям координат.

А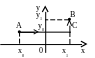 налогичные утверждения имеют место и для интеграла

г

Рис. 8

де АВ – пространственная кусочно-гладкая кривая, целиком лежащая в односвязной открытой области  пространства Oxyz, в которой функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны вместе со своими частными производными первого порядка. При этом к тождеству, имеющемуся в утверждении 3, добавляются еще следующие:

Функцию u = u(x, y) (см. п.4) часто называют потенциальной (первообразной) функцией для дифференциального выражения Pdx+ Qdy. Она может быть найдена по формуле (см. 21А):

( 22)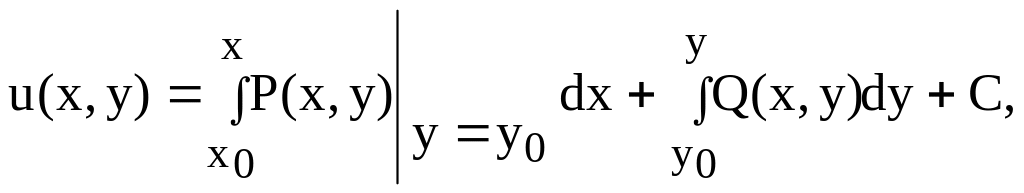

где (x₀; y₀) – любая фиксированная точка области ; (x; y) – переменная текущая точка; С – произвольная постоянная.

Из формулы ( 22) следует, что криволинейный интеграл равен разности значений потенциальной функции в конечной и начальной точках пути интегрирования, т.е.

( 23)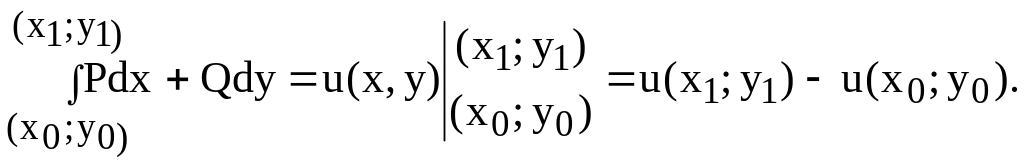

Пример 13.

Вычислить интеграл , где АВ – верхняя половина окружности x² + y² = 4, пробегаемая от точки А (-2;0) до точки В (2;0) (рис. 9).

Заметим вначале, что функции P(x,y) = x² и Q(x, y) = y² непрерывны и дифференцируемы на плоскости Oxy, а затем вычислим производные Q/x и P/y. Получим:

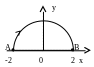
Следовательно, искомый интеграл не зависит от пути интегрирования. Заменим дугу АВ отрезком АВ оси Ox. В этом случае y = 0, dy = 0 и, следовательно,

Рис. 9

Пример 14.

Вычислить интеграл от А(1;1) до В(0;0) по линии L:

П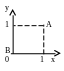 опытка вычисления данного интеграла вдоль линии со столь сложным уравнением любым из рассмотренных выше способов приведет к немалым, а главное, неоправданным, трудностям.

В некоторых достаточно часто встречающихся в приложениях случаях криволинейный интеграл второго рода может быть вычислен по формуле, являющейся обобщением формулы Ньютона-Лейбница.

Е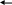 сли Pdx + Qdy является полным дифференциалом некоторой функции H = H(x,y), т.е. dH = Pdx + Qdy,

т

Рис. 10

о

В нашем случае поэтому по формуле (23)

Пример 15.

Вычислить интеграл , где – верхняя половина окружности x² + z² = 4, пробегаемая по ходу часовой стрелки и лежащая в плоскости xOz.

В данном случае P = x², Q = z², и так как то результат интегрирования не зависит от пути.

Интегрирование по верхней половине окружности заменим интегрированием по отрезку оси Ox, соединяющему точки пересечения окружности А (-2;0) и В (2;0) с осью Ох. На этом отрезке z = 0 и dz = 0, а х меняется от –2 до 2. Следовательно,

Пример 16.

Вычислить интеграл , где – окружность (x-1)² + (y-1)² = 1, пробегаемая против хода часовой стрелки.

Контур замкнутый:

, ,

поэтому по формуле Грина данный интеграл равен нулю.

Пример 17.

Показать, что есть полный дифференциал некоторой функции и восстановить эту функцию.

P’_y = -(x + y)^-2, Q’_x = -(x + y)^-2, т.е. условие 3 выполнено.

В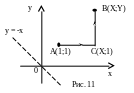 то же время P, Q, P’_y и Q’_х – элементарные функции и потому непрерывны всюду, где определены, т.е. вне прямой y = -x. Поэтому является полным дифференциалом в любой односвязной области D, не пересекающейся с прямой y = -x. Возьмем, например, в качестве области D верхнюю полуплоскость, ограниченную y = -x, и восстановим функцию, дифференциалом которой является заданное выражение. Для этого фиксируем в D какую-нибудь точку, например, А(1;1). Тогда в произвольной точке В(X;Y) значение искомой функции Н может быть вычислено с помощью криволинейного интеграла по формуле (19):

Так как данный интеграл не зависит от пути интегрирования в силу условия Q’_x = P’_y, он может быть вычислен, например, по линии, состоящей из отрезков, параллельных осям координат:

Учитывая, что на АС y = const = 1,а х меняется от1 до Х, имеем:

На СВ x = X = const, а y меняется от1 до Y, поэтому имеем:

Таким образом,

H(X, Y) = H(B) = H(A) + ln(X+1) – ln2 + ln(X+Y) – ln(X+1) = H(A) – ln2 + ln(X+Y).

Или, в привычных обозначениях:

H(x, y) = ln(x+y) + C, где C = H(A) – ln2.

Константа С может быть произвольной, так как функции, отличающиеся на постоянную, имеют равные дифференциалы.

Ответ: H(x, y) = ln(x+y) + C.

Пример 18.

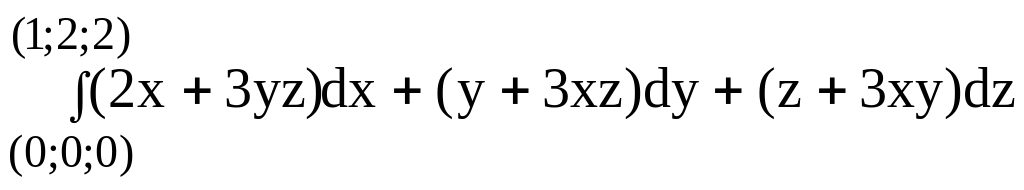
(проверить НПИ).

Рис. 12