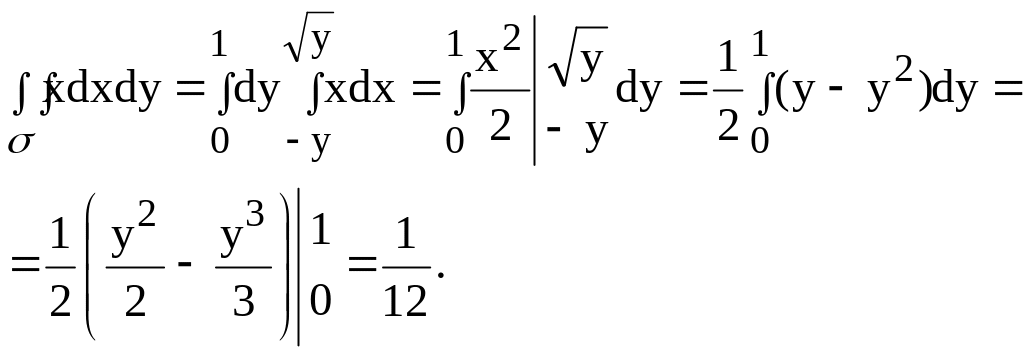IV. Общая схема построения интегралов.

IV. А Двойные и тройные интегралы.

Некоторые сведения из теории. Типовые задачи.

Вспомним, как мы вводим понятие определенного интеграла. Мы говорим: пусть на некотором интервале [a; b] задана функция одной независимой переменной f(x). Проделаем 5 операций:

1. Разобьем интервал [a; b] на n частей х₁, х₂,…,х_n, не имеющих между собой общих внутренних точек. Обозначим наибольший из отрезков х_k, k = 1, 2, .., n через , т.е. .

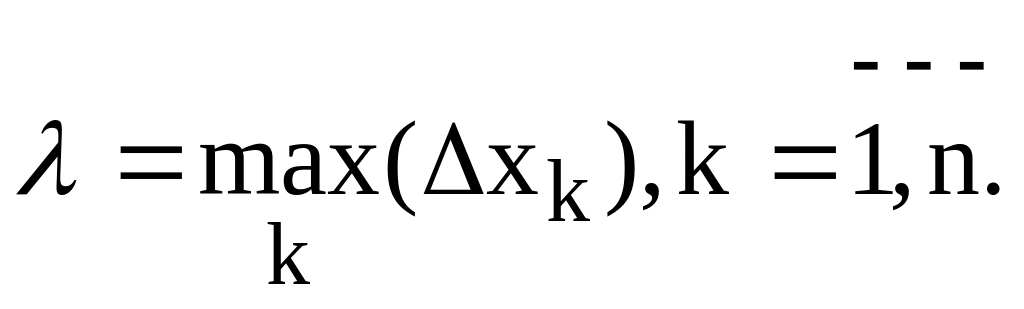2. Выберем в каждом из частных интервалов х_k произвольно по точке _k и вычислим в них значения функции f(_k).

3. Вычислим произведения f(_k)х_k, k = .

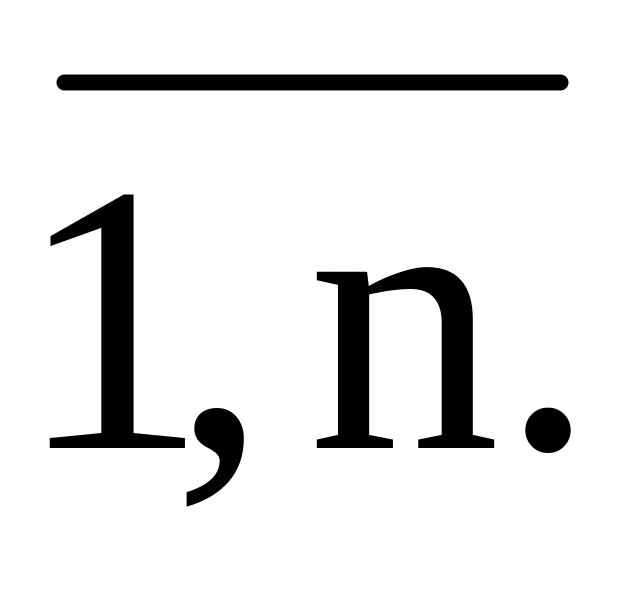4. Найдем сумму 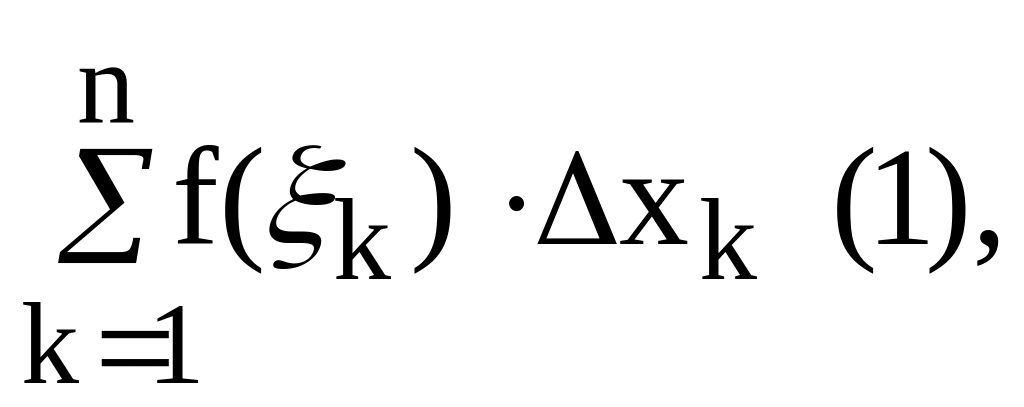которую называют интегральной суммой (суммой Римана) для функции f(x) на интервале [a; b], отвечающей данному дроблению интервала [a; b] на части и выбору точек (_k).

5. Измельчая дробление, ищем предел для (1), т.е.

( 2)

Если существует конечный предел ( 2), не зависящий ни от способа дробления интервала [a; b] на части, ни от выбора точек _k, то этот предел называется определенным интегралом от функции f(х) на интервала [a; b] и обозначается символом:

Итак, по определению:

( 3)

Г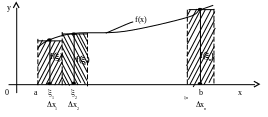 еометрически это выглядело как решение задачи о нахождении площади под кривой f(x) на интервале [a, b].

Именно в этом состоит геометрический смысл определенного интеграла.

Все рассматриваемые в данном разделе интегралы строятся именно по этой схеме: рассматривается функция, заданная в некоторой области, и производится пять операций. Отсюда и наименование раздела.

Двойной интеграл.

1. Построение и вычисление двойных интегралов в декартовых прямоугольных координатах.

Двойной интеграл представляет собой одно из возможных обобщений определенного интеграла на случай функции двух переменных. Дадим ему определение.

Пусть в плоской области  задана функция f(x, y). Проделаем 5 операций:

1. Разобьем область  на n частей ₁, ₂,…, _n, не имеющих между собой общих внутренних точек. Обозначим площади и диаметры этих частей соответственно через S₁, S₂,…, S_n и ₁, ₂, …, _n. Наибольший из диаметров обозначим через  и назовем ее рангом дробления, т. е.

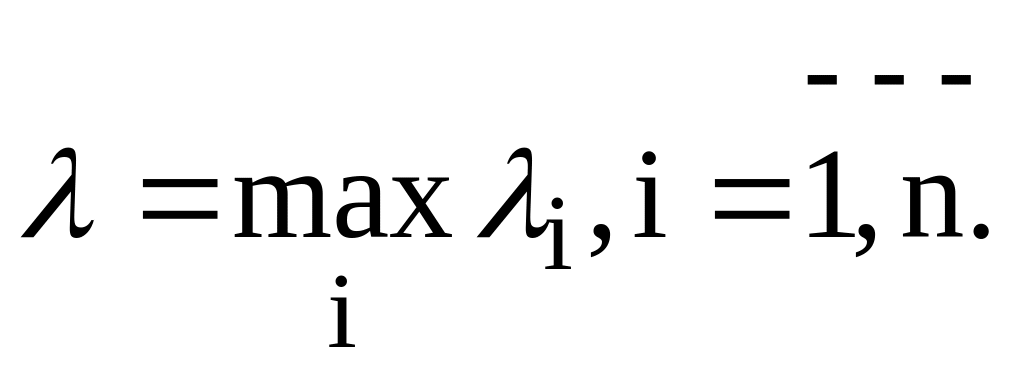
2. Выберем в каждой ячейке _k(k = 1, 2, …, n) произвольно по точке (x_k; y_k) и вычислим в них значения функции f(x, y), т.е. найдем числа f(x_k, y_k).

3. Вычислим произведения f(x_k, y_k)S_k(k = 1, 2, …, n).

4. Н

   ( 1)

   айдем сумму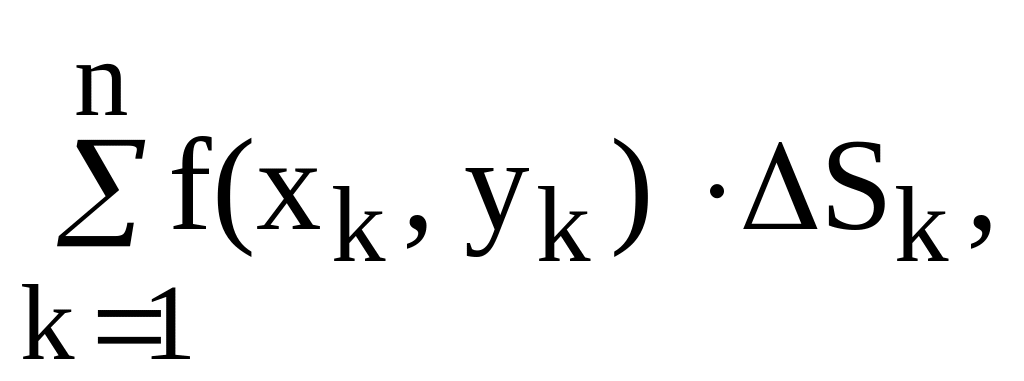 которую называют интегральной суммой для функции f(x, y) в области , отвечающей данному дроблению и выбору точек (x_k, y_k).

5. Измельчая дробление, ищем предел для (1), т.Е.

( 2)

Если существует конечный предел ( 2), не зависящий ни от способа дробления области  на части, ни от выбора точек (x₁, y₁), (x₂, y₂),…, (x_n, y_n), то этот предел называют двойным интегралом от функции f(x, y) по области  и обозначают символами:

или

При этом функцию f(x, y) называют подынтегральной функцией,  – областью интегрирования, x, y – переменными интегрирования, а d (или dxdy) – элементом площади.

Таким образом, по определению:

( 3)

Аналогичные построения двойного интеграла имеют место и тогда, когда область  лежит либо в плоскости xOz, либо в плоскости yOz. Например, если область  лежит в плоскости xOz, то получаем

Учитывая, что z = f(x, y) в пространстве определяет некоторую поверхность, проекция которой на плоскость xOy дает область , видим, что выражение f(x_k, y_k)S_k дает объем цилиндра, основание которого есть S_k, а высота равна f(x_k, y_k). Интегральная сумма равна сумме n объемов таких цилиндров. В пределе она дает объем тела, ограниченного сверху поверхностью z = f(x, y), снизу – областью , а с боков – цилиндрической поверхностью, направляющая которой – граница области , а образующая – прямая, параллельная оси Oz. В этом и состоит геометрический смысл двойного интеграла.

(*)

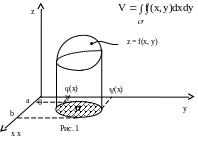
Перечислим простейшие свойства двойного интеграла, которые непосредственно следуют из его определения и доказываются аналогично соответствующим свойствам для определенного интеграла.

1. Если f(x,y) = 1 всюду в области , то 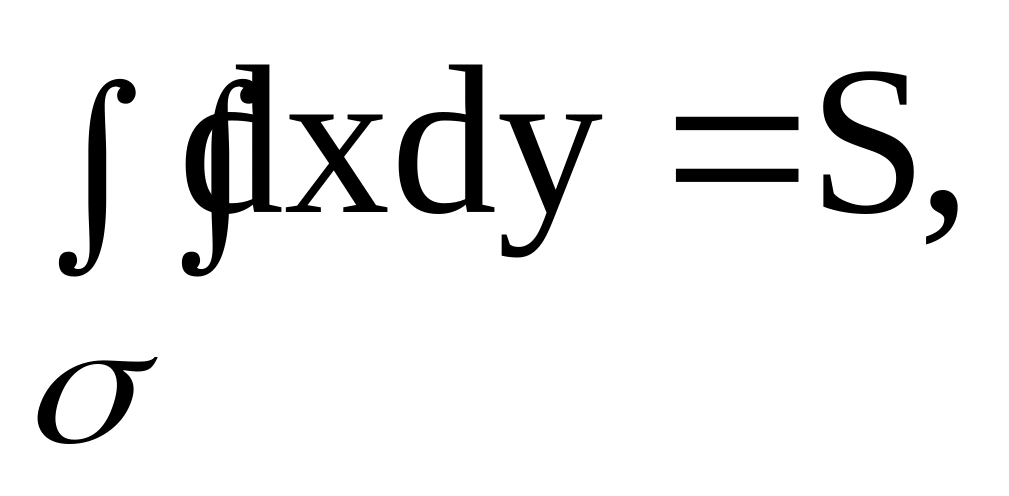где S означает площадь области .

2. Постоянный множитель k подынтегральной функции можно выносить за знак двойного интеграла:

3. Двойной интеграл от суммы двух функций равен сумме двойных интегралов от слагаемых:

Свойства 2 и 3 выражают свойство линейности двойного интеграла относительно подынтегральной функции.

4. Если область интегрирования  разбита на две части ₁ и ₂, то есть  =  ₁+ ₂, то

Это свойство называют свойством аддитивности двойного интеграла относительно области интегрирования.

5. Если всюду в области  функция f(x,y) удовлетворяет условию f(x, y)0, то

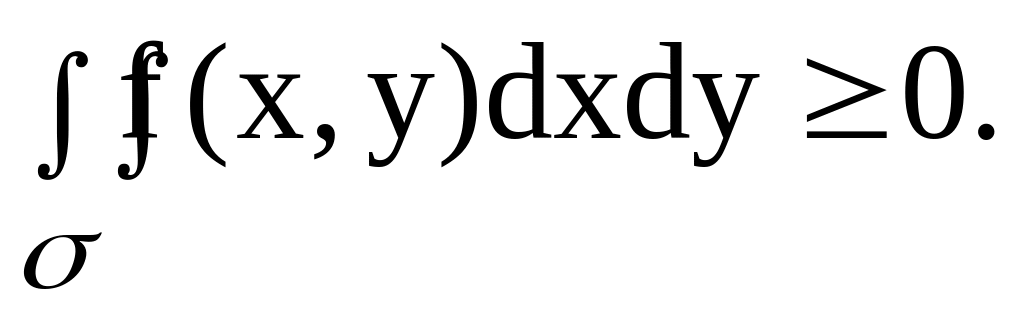
6. Если всюду в области  функции f(x, y) и (x, y) удовлетворяют условию f(x, y)  (x, y), то

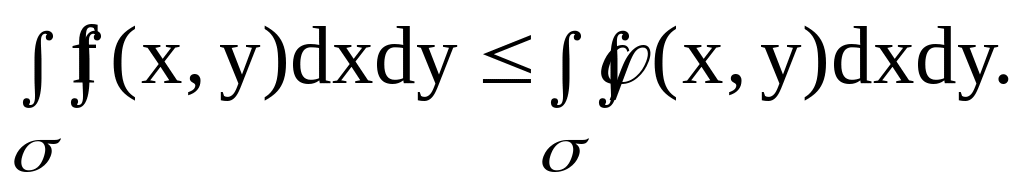
7. Имеет место неравенство:

8. (Теорема о среднем.) Если функция f(x, y) непрерывна в замкнутой области , то в этой области найдется хотя бы одна такая точка 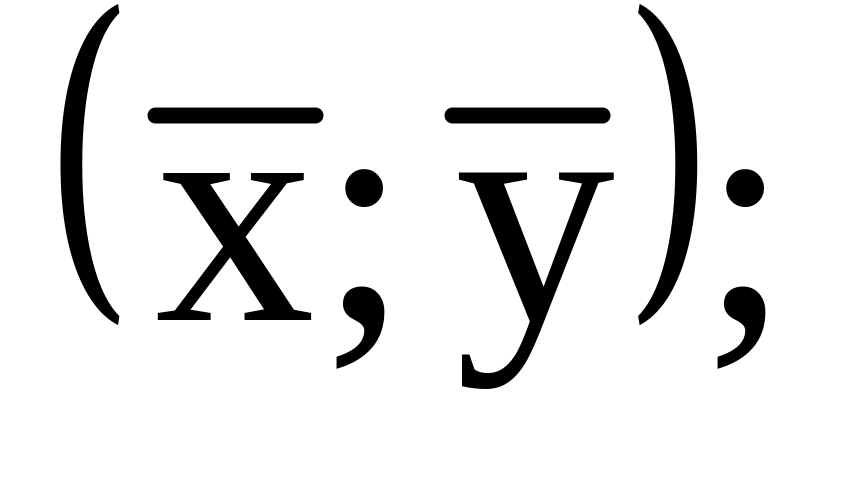что будет иметь место равенство:

где S означает площадь области .

Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.

Имеют место теоремы.

Т еорема 1.

Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями x = a, x = b, y = (x), y = (x) (здесь a < b, а функции (x)и (x) непрерывны на промежутке [a, b] и удовлетворяют условию (x)  (x)), то имеет место равенство:

( 4)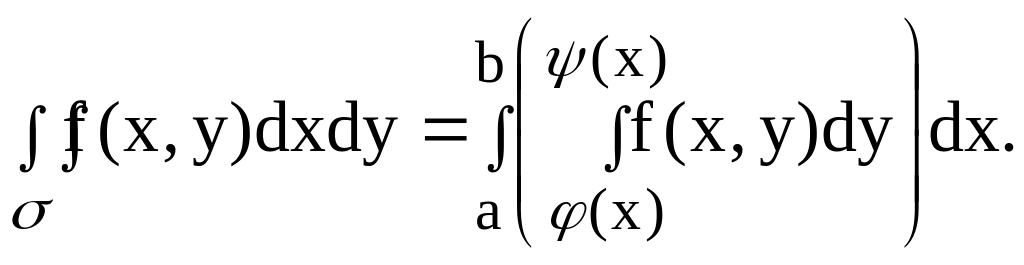

Выражение, стоящее в правой части равенства (4), называется повторным (двукратным) интегралом от функции f(x, y) по области , причем, пределы внешнего интеграла постоянны, а внутреннего – переменные (пределы внутреннего интеграла будут постоянны лишь в том случае, когда область  является прямоугольником со сторонами, параллельными осям координат).

Повторный интеграл, стоящий в правой части равенства (4), обычно записывают в виде:

( 5)

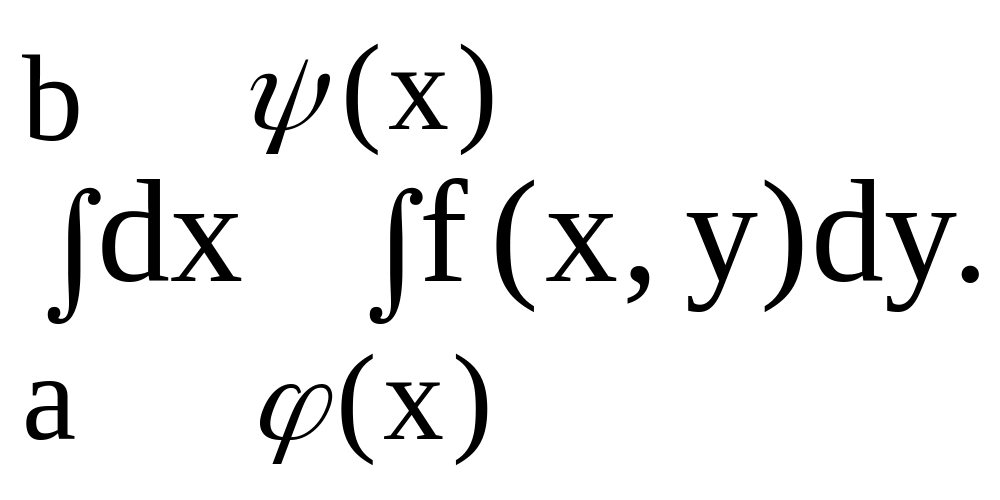
При вычислении двойного интеграла с помощью формулы (4) сначала вычисляется внутренний интеграл по переменной y

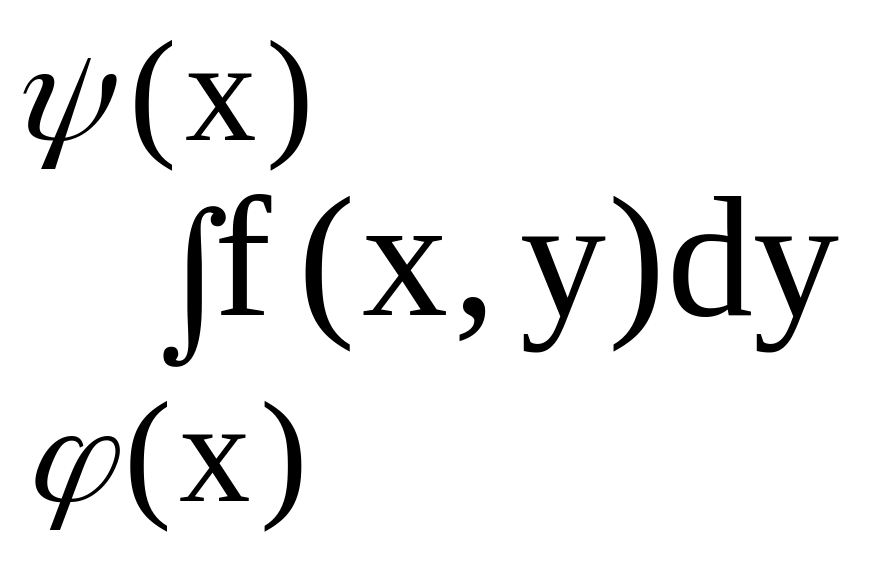
п ри постоянном значении переменной x, а затем полученная функция от х интегрируется по х в пределах от а до b.

При этом предполагается, что область  является правильной (простой) в направлении x = const (оси Oy), т.е. всякая прямая x = const, проходящая через внутренние точки области , пересекает границу этой области ровно в двух точках, причем, y = (x) и y = (x) – ординаты, соответственно, точки входа прямой в область и точки выхода из нее (рис. 2) (иначе, границы области  должны определяться аналитически не более чем двумя выражениями).

Рис.2

Т еорема 2.

Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями y = c, y = d, x = (y), x = (y) (здесь c >d, а функции (y) и (y) непрерывны на промежутке [c,d] и удовлетворяют условию (y)  (y)), то имеет место равенство:

( 6)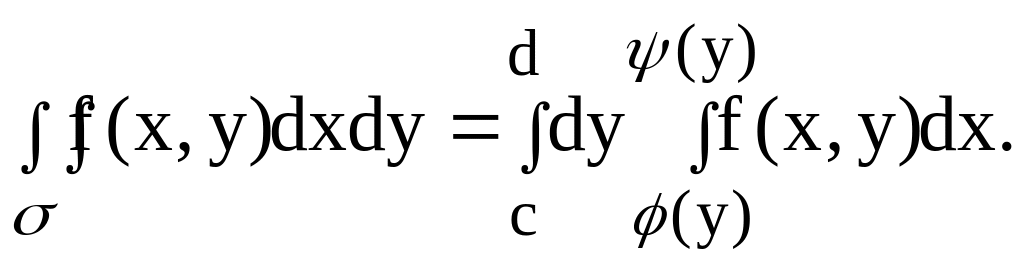

П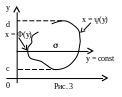 ри вычислении двойного интеграла с помощью формулы ( 6) сначала вычисляется внутренний интеграл 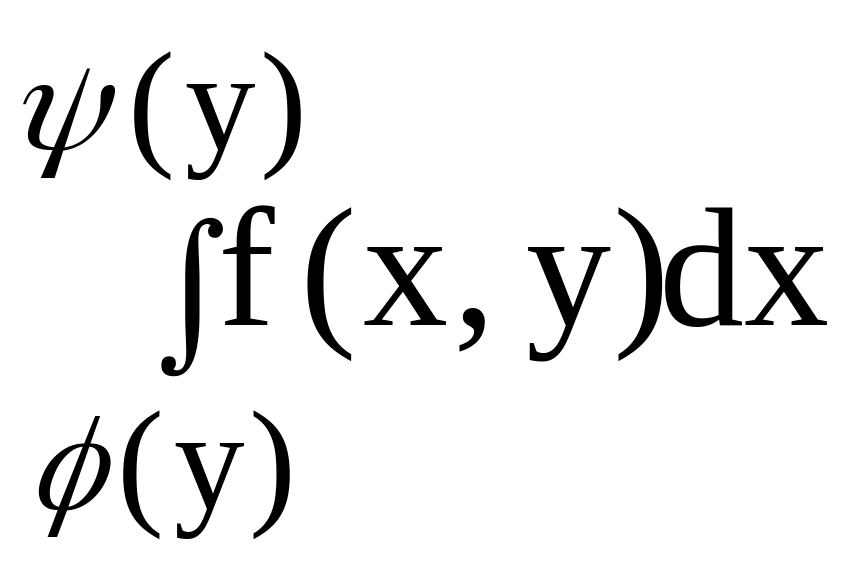при постоянном значении переменной y, а затем полученная функция от y интегрируется по y в пределах от c до d.

П ри этом предполагается, что область  является правильной (простой) в направлении y = const (оси Ox), т.е. всякая прямая y = const, проходящая через внутренние точки области, пересекает границу этой области ровно в двух точках, причем, (y) и (y) – ординаты, соответственно, точки входа прямой в область и точки выхода из нее (рис. 3).

Если область интегрирования  имеет более сложный вид, то ее следует разбить на конечное число частей, каждая из которых удовлетворяет условиям теоремы 1 или 2. Интеграл по области  заменяется при этом суммой интегралов по ее частям.

Заметим в заключение, что прежде чем решить вопрос об использовании либо формулы ( 5), либо ( 6), следует изобразить область  графически и выбрать, какая из переменных x или y будет внешней переменной интегрирования, а какая внутренней.

Пример 1.

В ычислить двойной интеграл по прямоугольной области , ограниченной прямыми x = 1, x = 2, y = 0, y = 2.

В ычисляем данный интеграл по формуле ( 5):

Внутренний интеграл вычисляем, считая x постоянным (т. е. по у):

Полученную функцию от х интегрируем по отрезку [1, 2] по переменной х:

Обычно вычисления внутреннего интеграла отдельно не делают, а все выкладки записывают в одну строку следующим образом:

Такой записью мы и будем пользоваться в дальнейшем.

Пример 2.

Вычислить двойной интеграл если область  ограничена параболами z = y² и y = z².

Область  ( рис. 4) – простая относительно оси Oy. Она имеет нижнюю границу z = y² и верхнюю границу y = z², т.е. (перед радикалом ставим только знак «+», т.к. область  находится в той части области плоскости yOz, где z > 0).

При любом фиксированном значении y из отрезка [0, 1] z меняется от z = y² до , поэтому имеем:

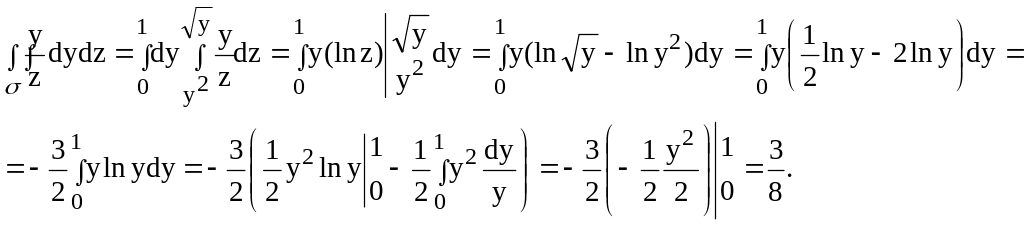Интеграл взят методом интегрирования по частям, причем при подстановке нижнего предела использован тот факт, что

Пример 3.

В

х = 2 + sin y

ычислить двойной интеграл если область  ограничена кривой x = 2 + siny и прямыми x= 0, y = 0, y = 2.

О бласть  (рис. 5) является простой относительно оси Oy. Левая ее граница x = 0, а правая x = 2+siny. При любом фиксированном значении y из отрезка [0, 2] x меняется от x = 0 до x = 2 + siny, поэтому по формуле ( 6) имеем:

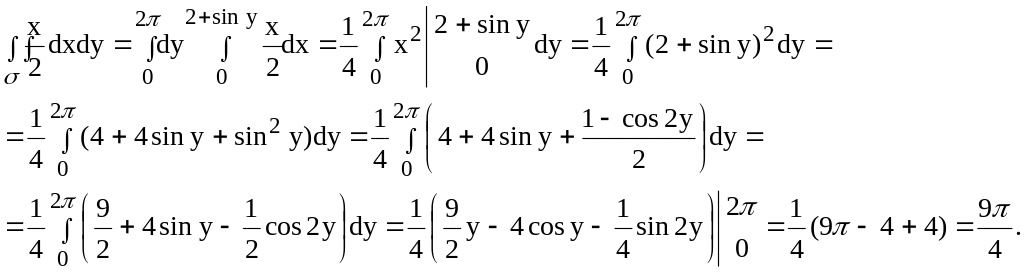
Пример 4.

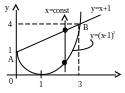
Вычислить интеграл , если область  ограничена линиями y = (x– 1)² и y = x + 1.

x



Изобразим область интегрирования для рассматриваемого интеграла ( рис.6). Координаты точек А и В находим, решая совместно уравнения линий, ограничивающих область интегрирования : А(0;1), В(3;4). Итак, координата х точек области меняется в пределах от 0 до3, и при каждом фиксированном х вторая координата y меняется от (x) = y₁(x) = (x-1)² до (x) = y₂(x) = x + 1.

Рис.6

Это позволяет записать искомый интеграл в виде ( 5):

Напомним, что при вычислении внутреннего интеграла «внешняя» переменная х считается постоянной:

Интегрируя теперь по «внешней» переменной и применяя для упрощения вычислений замены t = x + 1 и t = x – 1 в интегралах, получим:

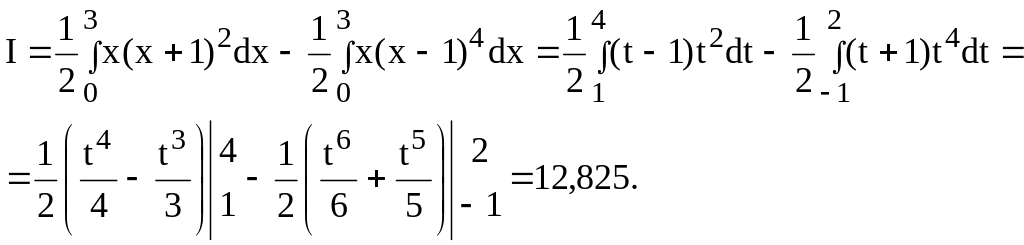
Пример 5.

В ычислить двойной интеграл если область  ограничена прямой y = x + 3 и параболой y = x² + 1.

И

Рис. 7

зобразим вначале область  (рис. 7). В этом примере разумно воспользоваться формулой ( 5), т.е. внешнее интегрирование проводить по х, а внутреннее – по y.

Н

-3

айдем теперь пределы изменения х, т.е. абсциссы точек пересечения данных линий. С этой целью приравняем правые части данных уравнений. Получаем: x² + 1= x + 3, откуда следует x² - x – 2 = 0. Корнями полученного квадратного уравнения являются числа –1 и 2 и, следовательно, в соответствии с формулой ( 5) имеем:

-3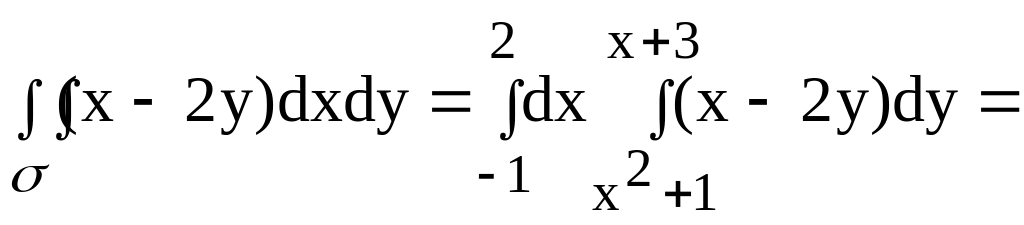

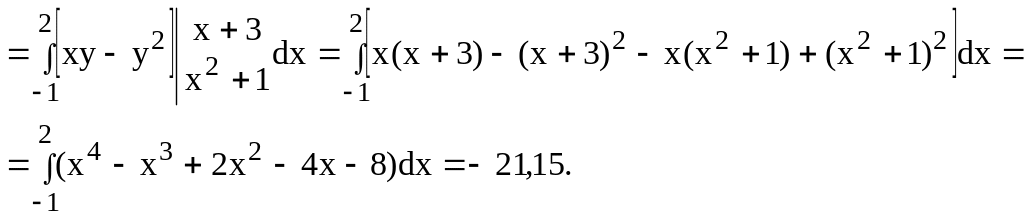
Пример 6.

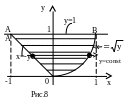
Вычислить интеграл по области , ограниченной линиями y = - x, y = 1, y = x² (рис. 8).

Записав уравнения линий АО и ОВ, соответственно, в виде x = -y и x = , легко заметить, что в этом примере выполнены условия теоремы 2. Поэтому можем написать: