4. Кривая на плоскости задана одним из трех способов: параметрически, в виде графика функции или неявно. Написать уравнения касательной и нормали в данной точке.

Найти уравнения касательной, удовлетворяющей некоторому условию.

Решение задачи для кривой, заданной параметрически.

В качестве примера кривой, заданной параметрически, рассмотрим кривую с радиус-вектором

(t)={at cos t, bt sin t}, a, b , .

1) Напишем уравнение касательной, проходящей через точку кривой при .

Уравнение касательной запишем сначала, например, в параметрическом виде. Для этого надо знать координаты точки кривой и направляющего вектора касательной.

Координаты точки кривой равны координатам вектора

В качестве искомого вектора возьмем касательный вектор к кривой

,

при

Параметрическое уравнение касательной прямой имеет вид

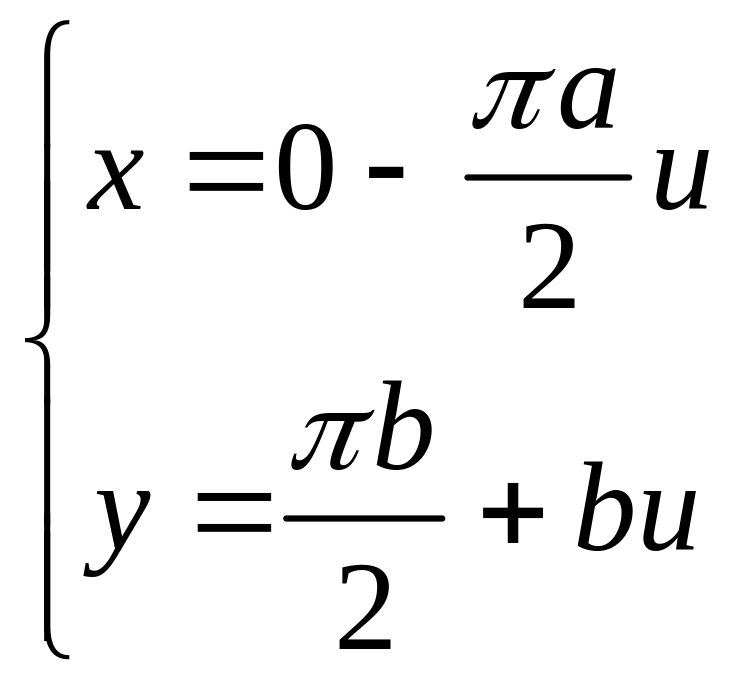
или

Общее уравнение касательной прямой можно найти из равенства

2) Напишем уравнение нормали к кривой, проходящей через точку при .

В качестве направляющего вектора нормали возьмем вектор

Мы выбираем вектор нормали так, чтобы скалярное произведение Напомним, что на плоскости задана прямоугольная система координат.

Уравнение нормали запишем в параметрическом виде

или

Из параметрического уравнения нетрудно получить общее уравнение нормали.

Решение задачи для кривой, заданной неявно.

В качестве примера кривой, заданной неявно, рассмотрим эллипс с уравнением или где

1. Напишем уравнение нормали, проходящей через точку .

В качестве направляющего вектора нормали возьмем вектор . Для этого найдем и вычислим его координаты в точке

.

Уравнение нормали к кривой в точке запишем в параметрическом виде

или

.

Это уравнение оси Oу.

2) Напишем уравнение касательной прямой как уравнение прямой, проходящей через данную точку перпендикулярно данному вектору : .

Получим

или

.

Решение задачи для кривой, заданной графиком функции.

Пусть поверхность задана в виде зависимости .

Тогда ее можно записать как параметрически

,

взяв в качестве параметра t координату x,

так и неявно

Мы свели задачу к рассмотренным случаям.

Заметим, что уравнение касательной можно искать также в виде , а уравнение нормали – в виде при .

5. Найти угол между кривыми в точке их пересечения:

а) и ,

б) и .

Решение.

Найдите точку пересечения кривых. Угол между кривыми – это угол между касательными к ним в точке пересечения. Воспользуйтесь формулой 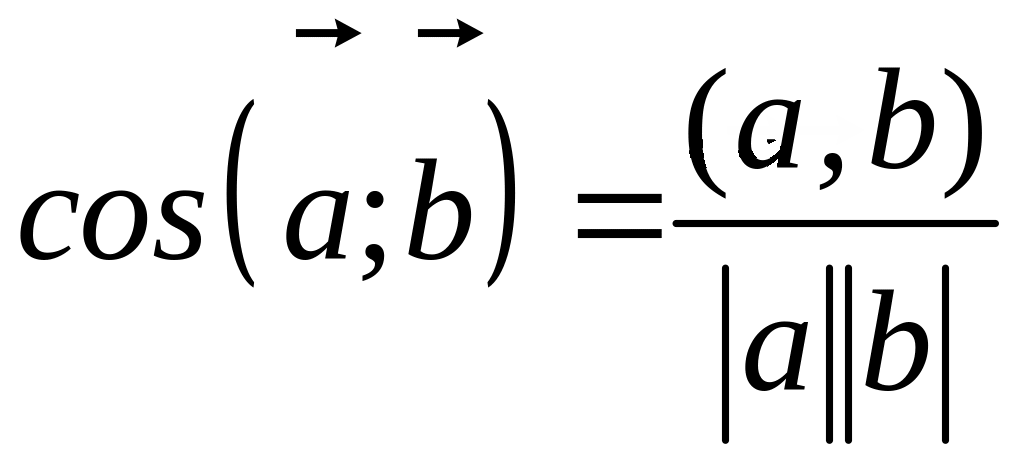, где и – касательные векторы к кривым в точке их пересечения.

6. Напишите уравнение касательной прямой и нормальной плоскости кривой , заданной параметрически в трехмерном пространстве, при :

.

Определите класс гладкости кривой.

Решение.

Чтобы определить класс гладкости кривой , выясним классы гладкости координатных функций . Так как функции , , являются аналитическими, то координатные функции являются аналитическими как произведения аналитических функций. Следовательно, кривая аналитическая.

Найдем уравнение касательной кривой в точке . При получаем точку кривой с координатами .

Найдем координаты вектора скорости кривой :

.

При получаем: . Имеем уравнение касательной в точке в параметрическом виде:

Уравнение плоскости, проходящей через точку и перпендикулярной вектору запишем в виде

. Точка нами уже найдена. Вектор – это вектор скорости кривой в точке также уже найден: . Получаем уравнение нормальной плоскости

, или .