§4. Длина кривой. Естественная параметризация кривой.

Рассмотрим гладкую кривую в пространстве ( на плоскости ).

Пусть r (t) - одна из ее - гладких параметризаций: и

Тогда длина кривой от значения параметра до значения параметра вычисляется по формуле

. (4.1)

Этот факт является одной из теорем математического анализа.

Замечание. Если длина кривой, вычисленная по указанной формуле, окажется отрицательной, то надо взять ее абсолютное значение.

Рассмотрим произвольную гладкую функцию замены параметра на кривой: , где причем и для любого . Напомним, что такие замены параметра называются допустимыми.

Тогда .

Теорема 4.1. Длина кривой не зависит от выбора параметра на кривой.

Рассмотрим функцию , значение которой для каждого t равно длине гладкой дуги от до t:

(4.2)

следовательно,

(4.3)

Итак, длина дуги s=s(t) есть возрастающая функция от t, которая является допустимой заменой параметра.

Определение 4.1. Естественным (или натуральным) параметром на кривой называется длина дуги, отсчитываемая от некоторой точки кривой. Параметризация кривой с помощью натурального параметра называется естественной параметризацией кривой.

§5. Формулы Френе. Кривизна и кручение кривой.

Пусть - гладкая кривая в пространстве (на плоскости ).

1. Рассмотрим касательный вектор , где s – натуральный параметр на кривой . Полагая в (4.3) t=s имеем , то есть вектор имеет единичную длину. Можно считать, что модуль вектора скорости относительно натурального параметра равен единице.

Вектор , , называется единичным вектором касательной.

2. Рассмотрим вектор . Он называется вектором кривизны кривой.

Выясним расположение вектора . Для этого воспользуемся традиционным для дифференциальной геометрии приемом: дифференцирование тождеств.

Рассмотрим тождество и продифференцируем его по s:

Это означает, что вектор кривизны перпендикулярен вектору касательной:

Замечание 5.1. Для любого вектора постоянной длины аналогично можно показать, что . (Проверьте.)

Для плоских кривых это означает, что является направляющим вектором нормали к кривой.

Для кривых в пространстве это означает, что вектор параллелен нормальной плоскости к кривой.

С другой стороны, вектор лежит в соприкасающейся плоскости (так как из замечания 3.1 следует, что соприкасающаяся плоскость параллельна векторам вне зависимости от выбора параметра на кривой). Следовательно, вектор является направляющим вектором главной нормали к кривой.

Найдем его длину .

Определение 5.1. Кривизной кривой в данной точке называется длина вектора кривизны в этой точке:

.

Рассмотрим вектор , .

Вектор , , называется единичным вектором нормали кривой в случае плоской кривой и единичным вектором главной нормали кривой в случае кривой в трехмерном пространстве.

Из определений кривизны и нормального вектора следует, что

. (5.1)

Мы определили кривизну кривой как функцию натурального параметра s. Можно считать, что кривизна – модуль вектора ускорения относительно натурального параметра.

Более наглядный смысл имеет следующее определение.

Определение 5.2. Пусть - гладкая кривая в пространстве . Пусть и М – две произвольные точки кривой. Рассмотрим касательные к кривой в точках и М. Обозначим через угол между касательными, а - длину кривой от М до .

Кривизной кривой в данной точке называется предел отношения

при стремлении :

.

Теорема 5.1. Определения 5.1 и 5.2 кривизны кривой эквивалентны.

Определение 5.3. Радиусом кривизны кривой в данной точке называется величина, обратная кривизне кривой в этой точке:

, если и , если

Следствие 5.1. Кривизна и радиус кривизны кривой являются геометрическими свойствами кривой и не зависят от выбора параметризации кривой.

Теорема 5.2. Для того чтобы гладкая кривая была прямой, отрезком или лучом необходимо и достаточно, чтобы кривизна равнялось нулю в каждой точке этой кривой.

Следствие 5.2. Кривизна кривой является мерой отклонения кривой от ее касательной.

Пример. Кривизна дуги окружности радиуса R во всех точках равна (Проверьте.)

3. Для кривых в трехмерном пространстве рассмотрим вектор .

Он имеет единичную длину как векторное произведение взаимно ортогональных единичных векторов .

Вектор , , называется единичным вектором бинормали кривой.

4. Пусть кривая плоская. Тогда к каждой ее точке М можно присоединить два взаимно перпендикулярных единичных вектора .

Совокупность М , называется репером Френе плоской кривой.

Зависимость векторов от векторов описывается формулами Френе для плоской кривой.

Пусть кривая не плоская. Тогда к каждой ее точке М можно присоединить три взаимно перпендикулярных единичных вектора .

Совокупность М, также называется репером Френе для кривой в трехмерном пространстве.

Зависимость векторов от векторов описывается формулами Френе для кривой в пространстве.

При перемещении точки М по кривой перемещается и репер Френе, поэтому его часто называют подвижным репером.

Вместе с репером Френе по кривой перемещается сопровождающий трехгранник Френе. Напомним, что совокупность М, определяет соприкасающуюся плоскость, совокупность М, - нормальную плоскость, а совокупность М , - спрямляющую плоскость.

Рисунок 13.

5. Выведем формулы Френе для плоской кривой .

Первая из формул Френе нами уже получена. Это формула (5.1):

.

Найдем вектор .

В силу замечания 5.1 вектор . Для векторов на плоскости это означает коллинеарность векторов и :

.

Найдем коэффициент пропорциональности .

Рассмотрим тождество

и продифференцируем его по параметру s:

Подставим и :

,

Теорема 5.3. Формулы Френе для кривых на плоскости.

Пусть - гладкая кривая на плоскости и r (s) - ее естественная параметризация.

Пусть - единичные векторы касательной и нормали.

Тогда

(5.2)

Следствие 5.3. .

6. Выведем формулы Френе для кривой в трехмерном пространстве.

Первая из формул Френе - это та же формула (5.1):

.

Найдем векторы и .

В силу замечания 5.1 векторы , . Для векторов трехмерного пространства это означает компланарность векторов и спрямляющей и соприкасающейся плоскостям соответственно:

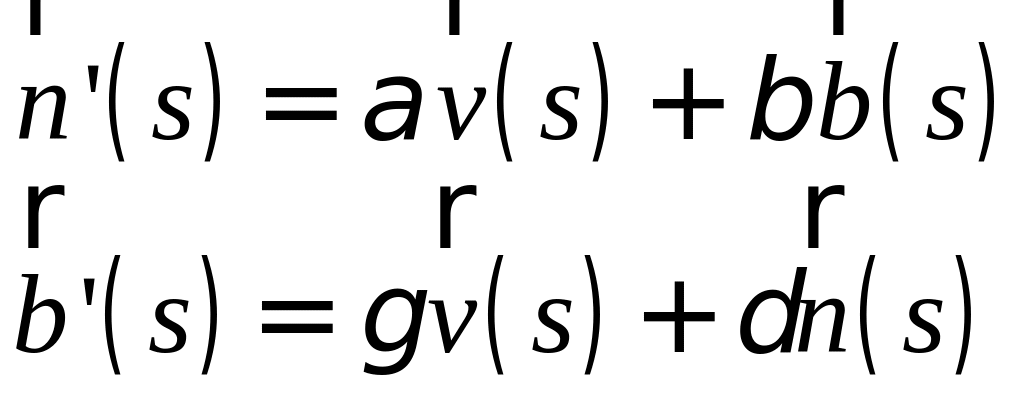, где

Найдем коэффициенты

Рассмотрим знакомое тождество

и продифференцируем его по параметру s:

Подставим и :

,

Мы получили .

Рассмотрим тождество

и также продифференцируем его по параметру s:

.

Подставим и :

,

,

.

Итак,

Переобозначим коэффициент через .

Определение 5.4. Кручением кривой в данной точке называется длина вектора , где - единичный вектор бинормали кривой, s - натуральный параметр на кривой:

.

Мы определили кручение кривой как функцию натурального параметра s. Более наглядный смысл имеет следующее определение.

Определение 5.5. Пусть - гладкая кривая в пространстве . Пусть и М – две произвольные точки кривой. Рассмотрим соприкасающиеся плоскости к кривой в точках и М и соответствующие нормали к ним (бинормали к кривой в точках и М ). Обозначим через угол между бинормалями, а - длину кривой от М до .

Кручением кривой в данной точке называется предел отношения

при стремлении :

.

Теорема 5.4. Определения 5.4 и 5.5 кривизны кривой эквивалентны.

Следствие 5.4. Кручение кривой является геометрическим свойствами кривой и не зависит от выбора параметризации кривой.

Теорема 5.5. Формулы Френе для кривых в трехмерном пространстве.

Пусть - гладкая кривая в трехмерном пространстве и r (s) - ее естественная параметризация.

Пусть - единичные векторы касательной, нормали и бинормали.

Тогда

(5.3)

Следствие 5.4. .

Теорема 5.6. Для того чтобы гладкая кривая была плоской необходимо и достаточно, чтобы кручение равнялось нулю в каждой точке этой кривой.

Следствие 5.6. Кручение кривой является мерой отклонения кривой от соприкасающейся плоскости.

7. Выпишем выражения кривизны и кручения кривой через радиус-вектор кривой , где s – натуральный параметр на кривой, и его производные.

Для кривизны:

. (5.4)

Выпишем первую формулу Френе (5.1) и продифференцируем ее по параметру s:

,

.

Подставляя вторую формулу Френе, получим

Вычислим также векторное произведение

.

Найдем смешанное произведение

Следовательно, для кручения

(5.5)

Теорема 5.7. Пусть и - любые гладкие функции, причем, Тогда существует и притом единственная с точностью до движения пространства гладкая кривая, для которой является кривизной, а - кручением в точке, соответствующей натуральному параметру s.

Определение 5.6. Систему равенств называют натуральными уравнениями кривой.

Из теоремы 5.7 следует, что натуральные уравнения кривой определяют кривую с точностью до движения пространства.