§1. Понятие кривой, ее гладкость и параметризации

Кривая линия является одним из основных объектов, рассматриваемых в дифференциальной геометрии.

Наглядное понятие «кривая» при точных описаниях приводит к нескольким разным определениям. В первом целом классе таких определений кривая является множеством точек с определенной очередностью их прохождения. При этом могут появиться «кратные точки», проходимые повторно. В определениях второго типа есть только некоторое множество точек. Часто, не уточняя само понятие кривой, говорят об употребительных способах задания кривой: параметрическом с помощью векторной функции r = r (t); неявном на плоскости как решении уравнения F (x; y) = 0; неявном в пространстве как решении системы уравнений F (x; y; z) = 0 и G(x; y; z) = 0; а также на плоскости графиком функции y = f (x) и так далее.

Выбор способа задания кривой часто связан с происхождением объекта исследования, и переход к другим вариантам иногда не допустим или труден, или не желателен. Многие задачи необходимо уметь решать непосредственно при каждом из способов задания кривой.

Напомним, что функция одного переменного f(x) принадлежит классу гладкости (или непрерывна) на числовом промежутке I, если f непрерывна в каждой точке этого промежутка. Записывают или просто .

Замечание. Непрерывность (принадлежность отображения классу ) интуитивно означает, что не происходит разрыва промежутка I при отображении. Более точно, отображение непрерывно, если и только если полный прообраз любого открытого подмножества образа является открытым множеством. Из курса математического анализа следует, что непрерывность отображения r (t) равносильна непрерывности всех координатных функций .

Функция одного переменного f(x) принадлежит классу гладкости (или k – дифференцируема) на промежутке I, где k – натуральное число или если f имеет непрерывные производные до порядка k включительно в каждой точке этого промежутка. Записывают или просто . При функция также называется аналитической.

Под числовым промежутком мы понимаем интервал, отрезок, полуинтервал, луч с началом или без начала или всю числовую прямую.

Рассмотрим трехмерное евклидово пространство . Пусть в нем фиксирована прямоугольная система координат Оxyz. Вместо трехмерного пространства можно также рассматривать евклидову плоскость . Факты относящиеся только к плоскому случаю, мы будем оговаривать дополнительно.

Векторная функция одного переменного принадлежит классу гладкости (или непрерывна) на промежутке I, если r (t)

непрерывна в каждой точке этого промежутка.

Записывают или просто .

Можно доказать, что векторная функция одного переменного непрерывна на промежутке I тогда и только тогда, когда каждая из координат является непрерывной функцией одного переменного в каждой точке этого промежутка.

Векторная функция одного переменного принадлежит классу гладкости (или k раз непрерывно-дифференцируема) на промежутке I, где k – натуральное число или если r (t) имеет непрерывные производные до порядка k включительно.

Записывают или просто . При векторная функция также называется аналитической.

Можно доказать, что векторная функция одного переменного k раз непрерывно-дифференцируема на промежутке I тогда и только тогда, когда каждая из координат имеет непрерывные производные до порядка k включительно.

Определение 1.1. Параметризованной кривой в трехмерном пространстве называется непрерывное отображение числового промежутка в это пространство

(1.1)

которое каждому значению параметра сопоставляет точку пространства с координатами .

Система равенств

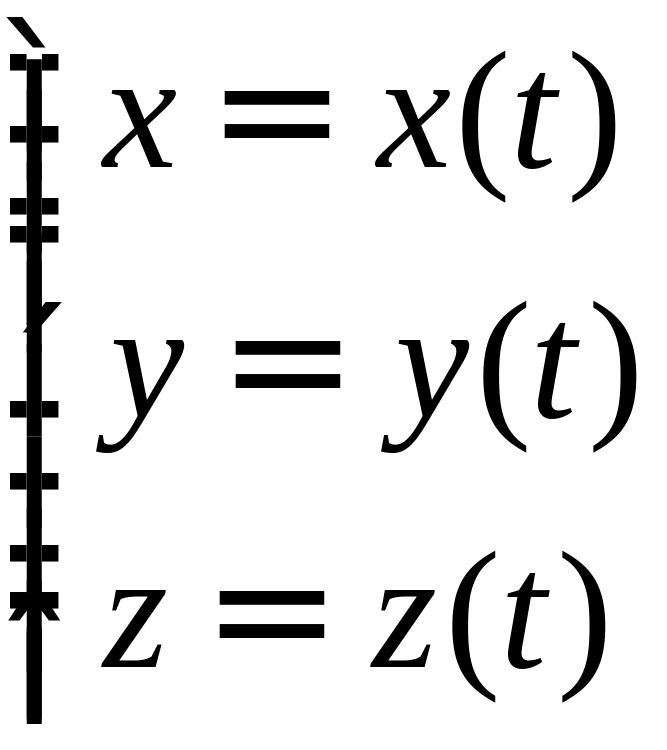, где ,

называется уравнениями кривой в параметрической форме.

Если отображение (1.1) является вложением (инъекцией), то говорят о простой параметризованной кривой.

Если отображение (1.1) инъективно лишь в достаточно малой окрестности каждой точки , то говорят о локально простой параметризованной кривой.

Определение 1.2. Две параметризованные кривые называют эквивалентными, если существует взаимно однозначное и взаимно непрерывное отображение (гомеоморфизм) , при котором

Определение 1.3. Класс эквивалентных параметризованных кривых называется геометрической кривой.

Фактически геометрическую кривую можно отождествлять с образом промежутка I в пространстве , что мы и будем делать в дальнейшем: . Эквивалентные параметризованные кривые являются различными параметризациями геометрической кривой.

Если потребовать в определении 1.2 чтобы отрезки и были ориентированы (направлены), а отображение сохраняло ориентацию, то факторизация эквивалентных в этом новом смысле параметризаций приводит к понятию направленной геометрической кривой.

Практически кривыми, определенными в 1.1 и 1.3, пользуются только при дополнительных ограничениях на вектор-функцию Еще Д.Пеано показал, что требование настолько слабое, что кривые в этом смысле могут заполнять весь квадрат на плоскости, куб в пространстве, что далеко уводит нас от насущных потребностей, ради которых непосредственно вводится термин «кривая».

Определение 1.4. Параметризованная кривая принадлежит классу гладкости , если задающая ее векторная функция принадлежит классу гладкости на этом промежутке.

Определение 1.5. Геометрическая кривая называется - гладкой (k раз непрерывно-дифференцируемой), где k - натуральное число или , если у каждой точки этой кривой есть такая окрестность , что пересечение имеет - гладкую параметризацию.

Для геометрических кривых класса гладкости замена параметра считается допустимой, если функция имеет на отрезке непрерывные производные до порядка k включительно и первая производная отлична от нуля во всех точках Для параметризованных кривых класса гладкости при определении их эквивалентности принято рассматривать только допустимые замены параметра.

Определение 1.6. - гладкая параметрическая кривая называют регулярной в точке , если

Определение 1.7. - гладкая геометрическая кривая называется регулярной, если у каждой точки этой кривой есть такая окрестность , что пересечение имеет регулярную параметризацию.

Некоторые геометрические кривые при подходящем выборе осей координат x, y ,z допускают параметризацию вида

Для плоских геометрических кривых это означает, что кривая является графиком некоторой функции Мы называем кривую плоской, если все ее точки принадлежат некоторой плоскости. Выбором декартовой системы координат Oxyz можно достигнуть, чтобы этой плоскостью стала плоскость Oxy.

Теорема 1.1. Пусть - геометрическая кривая и r (t) - одна из ее - гладких параметризаций, регулярная в точке :

причем

Тогда в достаточно малой окрестности точки кривая может быть задана уравнениями:

где и g - - гладкие функции от переменной х.

Замечание 1.1. Для плоских геометрических кривых теорема 1.1 задает достаточное условие, когда геометрическая кривая является графиком функции.

Наоборот, если плоская геометрическая кривая является графиком функции y=f (x), то одной из ее параметризаций является следующая: r . Такие кривые также можно задать неявно как решение уравнения .

Рассмотрим плоские геометрические кривые, заданные неявно как решение уравнения , где - гладкая функция переменных x, y.

Пусть в некоторой точке плоскости выполняется условие . Тогда в окрестности этой точки кривую можно представить в виде графика функции . Это следует из теоремы о неявной функции.

Определение 1.7. Множество точек пространства называется элементарной кривой, если это множество является образом интервала числовой прямой при его гомеоморфизме в пространство.

Следующие теоремы являются следствиями теоремы о неявных функциях.

Теорема 1.2. Пусть - гладкая функция переменных x, y.

Рассмотрим множество M всех точек плоскости Oxy, координаты которых удовлетворяют уравнению .

Пусть в некоторой точке этого множества

Тогда существует такая окрестность точки , что пересечение является элементарной кривой.

Замечание 1.2. Условие означает, что вектор в точке .

Теорема 1.3. Пусть - гладкие функции переменных x ,y ,z.

Рассмотрим множество M всех точек пространства, координаты которых удовлетворяют системе уравнений

Пусть в некоторой точке этого множества ранг матрицы

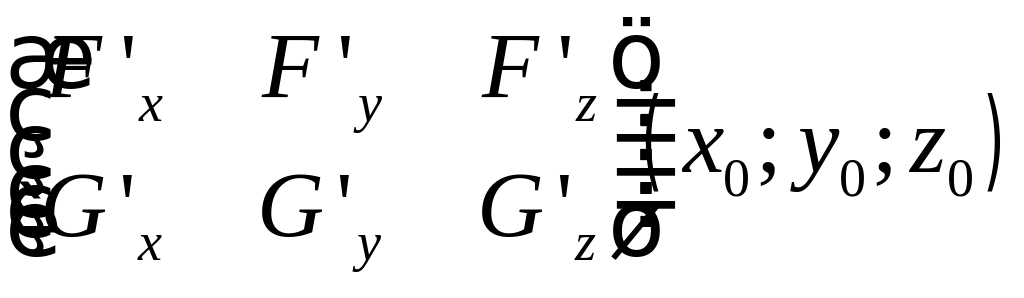
равен двум.

Тогда существует такая окрестность точки , что пересечение является элементарной кривой.

Замечание 1.3. Условие

означает, что векторы и grad G линейно независимы в точке .

В дальнейшем нас будут интересовать локальные свойства геометрических кривых. Мы будем называть их просто кривыми. Итак, если кривая плоская, то она может быть задана одним из трех способов: параметрически, неявно или как график функции (при выполнении условий теорем 1.1 и 1.2). Если же кривая расположена в трехмерном пространстве, то (при выполнении условий теорем 1.1 и 1.3) она может быть задана параметрически, а также как решение системы уравнений

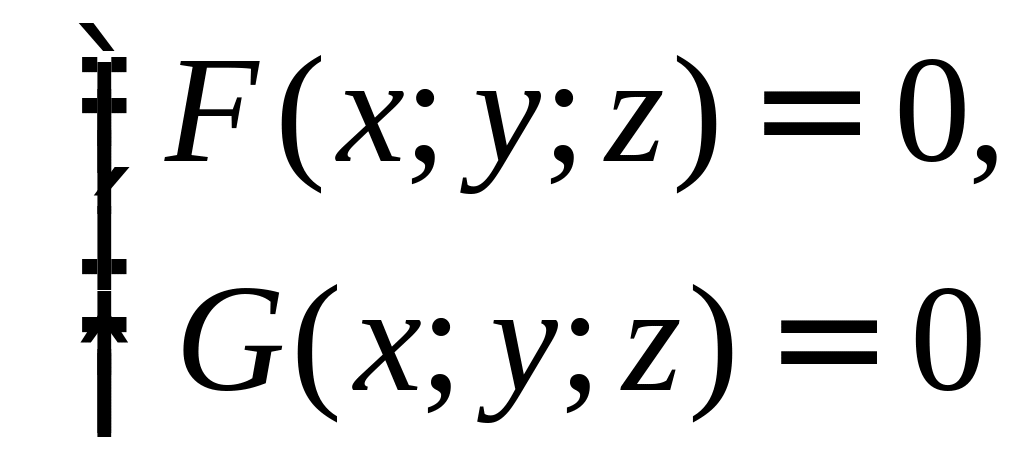или

Более точно, кривую в пространстве можно задать параметрически, а также как пересечение двух поверхностей, каждая из которых в свою очередь может быть задана параметрически, неявно как решение уравнения , или как график функции .