
- •Печатается по решению кафедры математического анализа и геометрии
- •Содержание
- •Предисловие
- •Введение
- •§1. Понятие кривой, ее гладкость и параметризации
- •§2. Касательная к кривой на плоскости и в пространстве. Угол между кривыми. Нормаль к кривой на плоскости и нормальная плоскость
- •§3. Сопровождающий трехгранник кривой (трехгранник Френе)
- •§4. Длина кривой. Естественная параметризация кривой.
- •§5. Формулы Френе. Кривизна и кручение кривой.
- •§6.Кинематический смысл кривизны и кручения
- •§7. Вычисление кривизны и кручения в произвольной параметризации.
- •§8. Задачи с решениями.
- •1. Доказать эквивалентность двух параметризованных кривых
- •3. Кривая в пространстве задана одним из способов: параметрически или в виде пересечения поверхностей. Выяснить расположение кривой в пространстве и по возможности нарисовать ее.
- •4. Кривая на плоскости задана одним из трех способов: параметрически, в виде графика функции или неявно. Написать уравнения касательной и нормали в данной точке.
- •5. Найти угол между кривыми в точке их пересечения:
- •6. Напишите уравнение касательной прямой и нормальной плоскости кривой , заданной параметрически в трехмерном пространстве, при :
- •7. Кривая задана как пересечение двух поверхностей:
- •8. Найти векторы канонического репера кривой
- •9. Кривая задана параметрическими уравнениями
- •10. Найти точки на кривой , в которых бинормаль параллельна плоскости .
- •11. Даны параметрические уравнения кривой на плоскости
- •12. Даны параметрические уравнения двух кривых на плоскости или в пространстве, проходящих через общую точку. Определить порядок касания кривых в этой точке.
- •14. Даны параметрические уравнения кривой на плоскости или в пространстве. Записать кривую через натуральный параметр s. Выяснить длину вектора r’(s) и направление вектора r”(s).
- •16. Даны параметрические уравнения кривой на плоскости или в пространстве. Найти кривизну и кручение кривой, не переходя к натуральному параметру.
- •§ 9. Задачи для самостоятельного решения.
- •§ 10. Тестовая работа по дифференциальной геометрии кривых
- •Вариант ab.
- •§ 11. Методические указания по изучению темы дифференциальная геометрия поверхностей в трехмерном пространстве.
- •Тема 1. Способы задания поверхностей. Касательная плоскость и нормаль к поверхности.
- •Поверхность в пространстве задана одним из трех способов: параметрически, в виде графика функции или неявно. Задать ее другими оставшимися способами.
- •Поверхность в пространстве задана одним из трех способов: параметрически, в виде графика функции или неявно. Написать уравнения касательной и нормали в данной точке.
- •Тема 2. Касание поверхностей.
- •Даны параметрические уравнения поверхности. Найти какую-нибудь поверхность, имеющую с данной поверхностью в данной точке касание 1, 2, 3 порядка.
- •Даны параметрические уравнения двух поверхностей, проходящих через общую точку. Определить порядок касания поверхностей в этой точке.
- •Тема 3. Первая квадратичная форма поверхности.
- •Поверхность задана параметрически. Найти первую квадратичную форму поверхности.
- •С помощью первой квадратичной формы найти длину кривой на поверхности, угол между кривыми и площадь области на поверхности.
- •Тема 4. Вторая квадратичная форма поверхности. Полная и средняя кривизны поверхности.
- •Тема 5. Первая и вторая квадратичные формы поверхности. Гауссова и средняя кривизны поверхности.
- •§ 12. Содержание курса Дифференциальная геометрия
- •2. Теория кривых в евклидовом пространстве
- •3. Теория поверхностей в евклидовом пространстве
- •Литература
§6.Кинематический смысл кривизны и кручения
С
каждой точкой М
кривой
в трехмерном пространстве связан вполне
определенный сопровождающий трехгранник
![]() образованный единичными векторами
касательной, главной нормали и бинормали,
исходящими из этой точки кривой. Из
построения сопровождающего трехгранника
следует, что его ориентация в любой
точке кривой совпадает с ориентацией
трехмерного пространства. Следовательно,
различные положения трехгранника
можно рассматривать как перемещение
твердого тела вдоль кривой.
образованный единичными векторами
касательной, главной нормали и бинормали,
исходящими из этой точки кривой. Из
построения сопровождающего трехгранника
следует, что его ориентация в любой
точке кривой совпадает с ориентацией
трехмерного пространства. Следовательно,
различные положения трехгранника
можно рассматривать как перемещение
твердого тела вдоль кривой.
Естественно выбрать наиболее простое движение по кривой – движение с постоянной по модулю скоростью, равной единице. В этом случае пройденный путь s равняется протекшему времени, то есть параметр s можно понимать как время.
Всякое перемещение твердого тела разложимо на два элементарных движения: а) параллельный перенос, когда все точки тела описывают равные векторы и б) поворот около неподвижной оси.
Выпишем основные уравнения теории кривых:
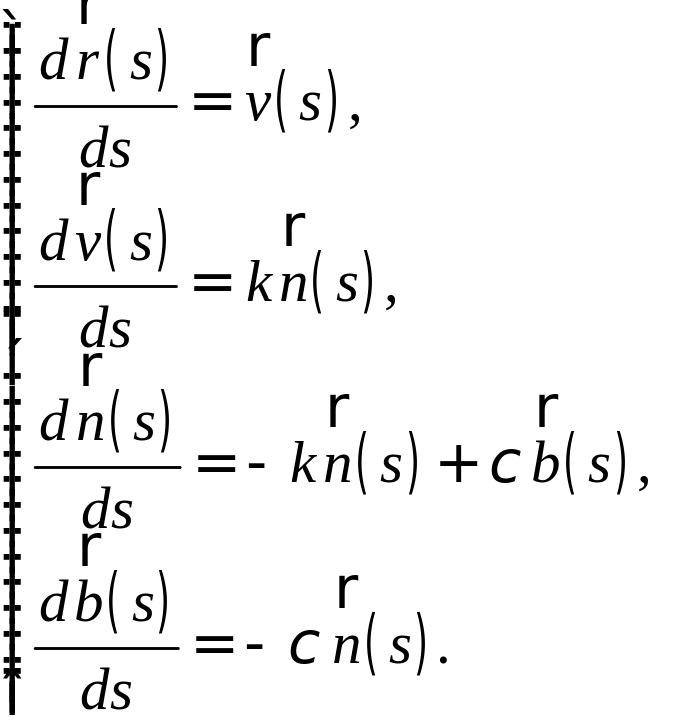 (6.1)
(6.1)
Скорость
поступательного движения его вершины
М
в момент времени s
равна
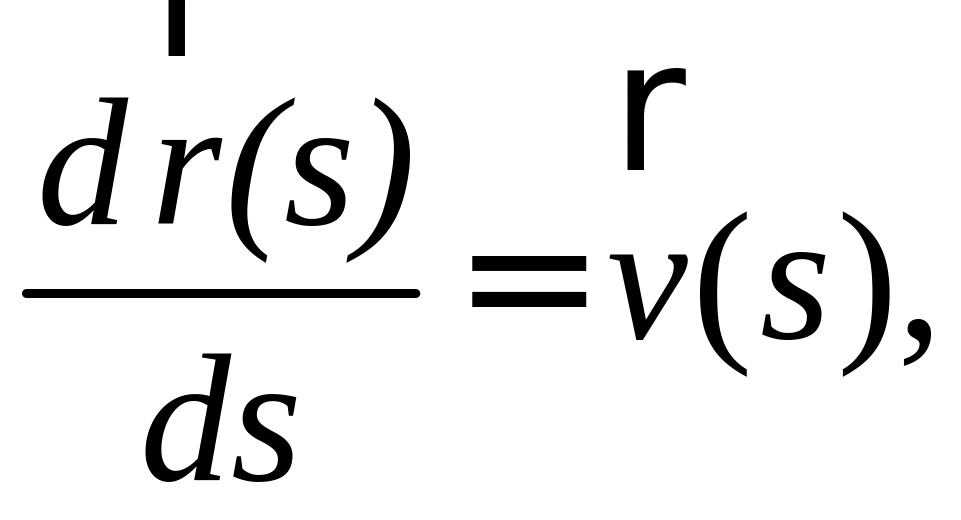 последние три уравнения в (6.1) определяют
линейные скорости точек, расположенных
в концах единичных векторов
последние три уравнения в (6.1) определяют
линейные скорости точек, расположенных
в концах единичных векторов
![]()
Пусть
![]() и
и
![]() - два произвольных вектора, закрепленных
в точке M,
причем
вектор
- единичный. Пусть вектор
вращается вокруг вектора
.
Пусть
- два произвольных вектора, закрепленных
в точке M,
причем
вектор
- единичный. Пусть вектор
вращается вокруг вектора
.
Пусть
![]() - линейная скорость конца вектора
.
Тогда
- линейная скорость конца вектора
.
Тогда
![]() .
.
Следовательно, считая вектором угловой скорости, имеем
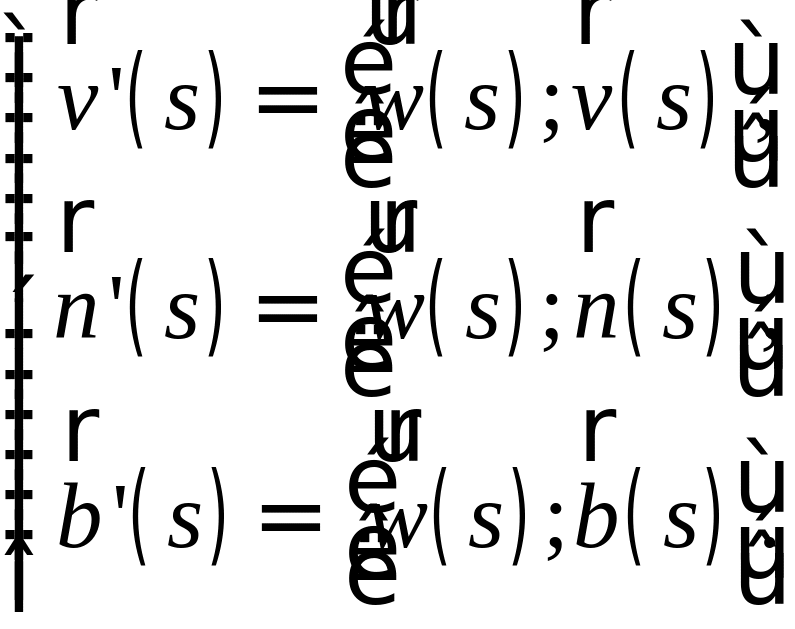 (6.2)
(6.2)
Пусть
вектор
![]() ,
где
,
где
![]() .
Подставляя это выражение в (6.2), получим
.
Подставляя это выражение в (6.2), получим
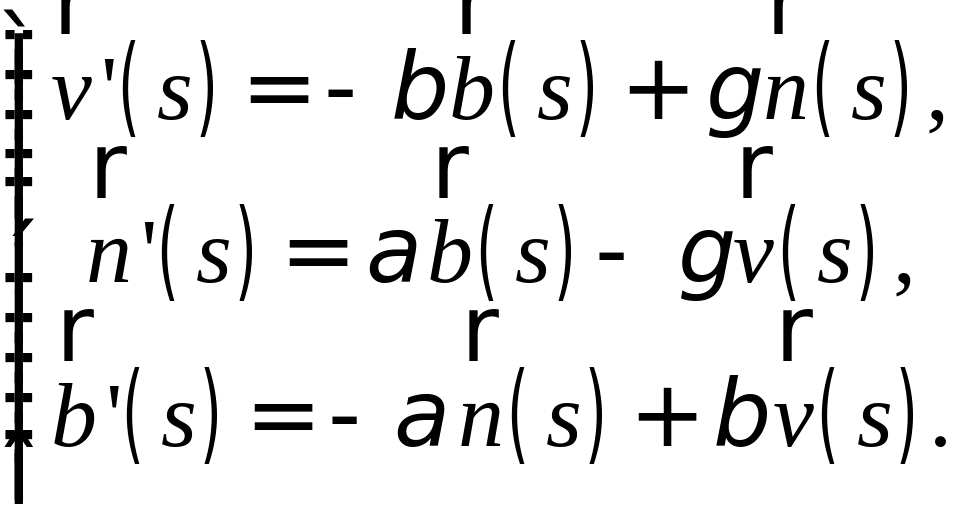 (6.3)
(6.3)
Сравнивая
(6.1) и (6.3), получим
![]()
Следовательно, для вектора угловой скорости
![]() .
.
Перепишем в более удобном для нас виде
![]() .
(6.4)
.
(6.4)
Итак,
вектор угловой скорости разлагается
на две компоненты -
![]() и
и
![]() .
Первой из них соответствует вращение
трехгранника в соприкасающейся плоскости
вокруг бинормали с угловой скоростью
.
Первой из них соответствует вращение
трехгранника в соприкасающейся плоскости
вокруг бинормали с угловой скоростью
![]() ,
а второй из них – вращение в нормальной
плоскости вокруг касательной с угловой
скоростью
.
,
а второй из них – вращение в нормальной
плоскости вокруг касательной с угловой
скоростью
.
В соответствии с этим представлением формулы Френе можно разбить на две группы формул:

В первом движении вектор бинормали постоянен. Во втором вращении постоянным является вектор касательной . Ось, на которой лежит вектор , является мгновенной осью вращения. Таким образом:
Главная нормаль – единственная прямая, по которой компоненты скорости вращения трехгранника Френе равны нулю.
Кривизна k - компонента скорости вращения вокруг бинормали.
Кручение равно с противоположным знаком компоненте скорости вращения вокруг касательной.
Если кривая плоская, то мы имеем мгновенное поступательное движение и мгновенное вращение, происходящие в плоскости кривой (соприкасающейся плоскости).
§7. Вычисление кривизны и кручения в произвольной параметризации.
Пусть - гладкая кривая в пространстве .
Пусть r (t) - одна из - гладких параметризаций кривой :
Рассмотрим
функцию замены параметра
![]() ,
где s
–
натуральный параметр.
,
где s
–
натуральный параметр.
Выведем формулу для кривизны кривой.
Для этого вычислим
![]() ,
,
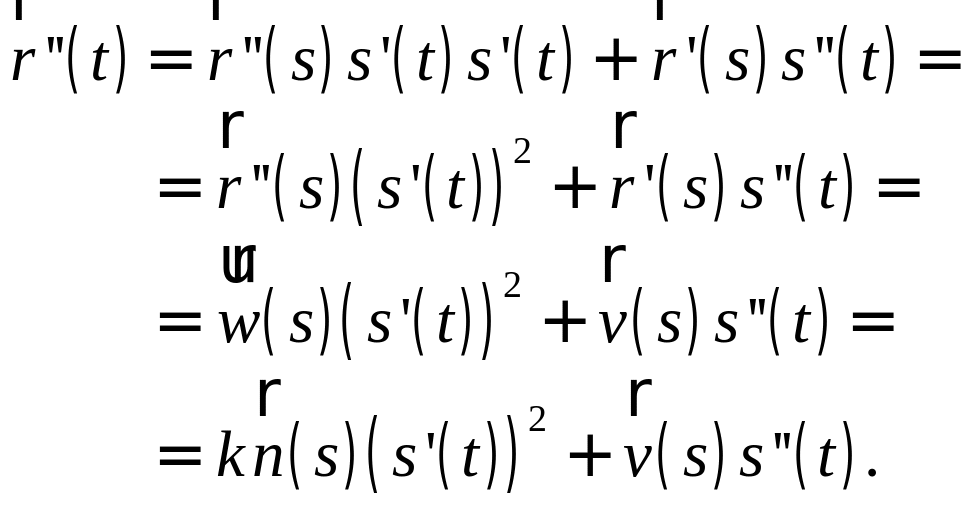
Из
последнего равенства видно, что вектор
![]() параллелен соприкасающейся плоскости,
порожденной векторами
параллелен соприкасающейся плоскости,
порожденной векторами
![]() и
и
![]() .
.
Естественно
ожидать, что векторное произведение
![]() коллинеарно бинормали
коллинеарно бинормали
![]() :
:
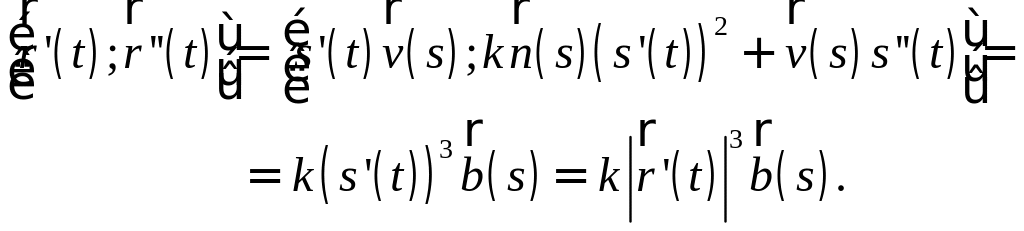
Взяв
последнее равенство по модулю, получим
(![]() ):
):
![]()
Следовательно,
 (7.1)
(7.1)
Для кривой на плоскости из формулы (7.1) получаем
 .
(7.2)
.
(7.2)
2.
Для
получения формулы для кручения найдем
разложение вектора
![]() по векторам
:
по векторам
:
![]()
![]()
Так как
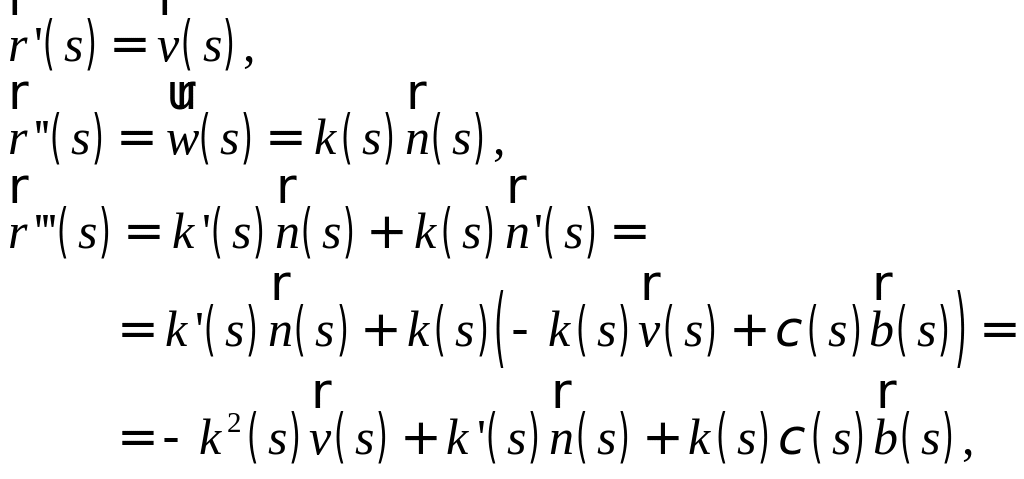
то
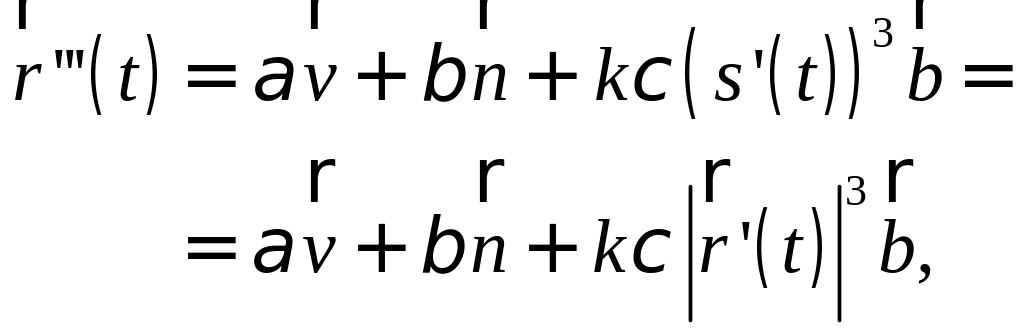
где числа и обозначают коэффициенты при и .
Найдем смешанное произведение
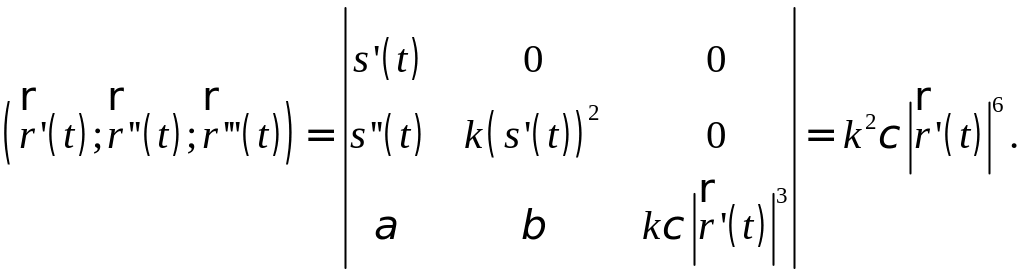
Подставляя в это выражение формулу (7.1) и выражая , получим
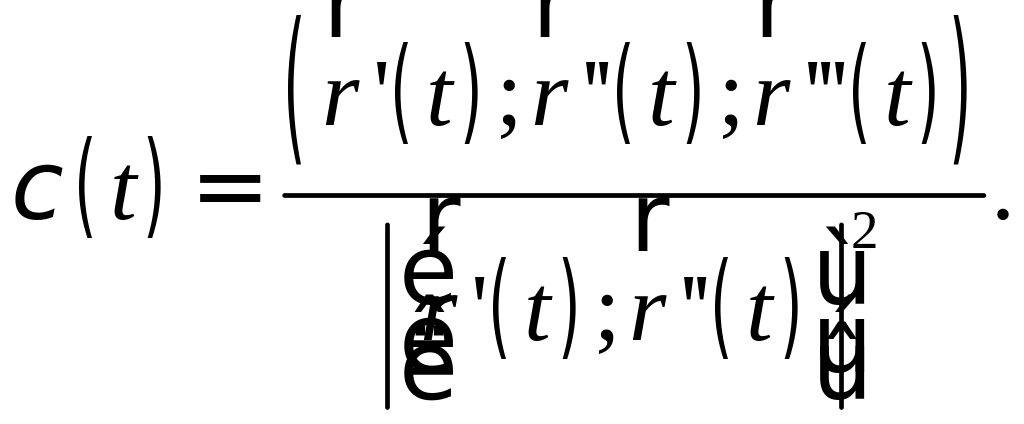 (7.3)
(7.3)
Формулу (7.3) можно получить и другим способом.
Возьмем формулу (5.5)
Вычислим
![]()
![]()
![]()
Пользуясь свойствами смешанного произведения, найдем
 (7.4)
(7.4)
Подставляя (7.1) и (7.4) в (5.5), получим (7.3).
Замечание
7.1.
Когда
мы переходим от
![]() к
к
![]() и наоборот, мы имеем в виду значения
параметров s
и
t,
соответствующие друг другу при замене
параметра
и
и наоборот, мы имеем в виду значения
параметров s
и
t,
соответствующие друг другу при замене
параметра
и
![]()
