
- •Печатается по решению кафедры математического анализа и геометрии
- •Содержание
- •Предисловие
- •Введение
- •§1. Понятие кривой, ее гладкость и параметризации
- •§2. Касательная к кривой на плоскости и в пространстве. Угол между кривыми. Нормаль к кривой на плоскости и нормальная плоскость
- •§3. Сопровождающий трехгранник кривой (трехгранник Френе)
- •§4. Длина кривой. Естественная параметризация кривой.
- •§5. Формулы Френе. Кривизна и кручение кривой.
- •§6.Кинематический смысл кривизны и кручения
- •§7. Вычисление кривизны и кручения в произвольной параметризации.
- •§8. Задачи с решениями.
- •1. Доказать эквивалентность двух параметризованных кривых
- •3. Кривая в пространстве задана одним из способов: параметрически или в виде пересечения поверхностей. Выяснить расположение кривой в пространстве и по возможности нарисовать ее.
- •4. Кривая на плоскости задана одним из трех способов: параметрически, в виде графика функции или неявно. Написать уравнения касательной и нормали в данной точке.
- •5. Найти угол между кривыми в точке их пересечения:
- •6. Напишите уравнение касательной прямой и нормальной плоскости кривой , заданной параметрически в трехмерном пространстве, при :
- •7. Кривая задана как пересечение двух поверхностей:
- •8. Найти векторы канонического репера кривой
- •9. Кривая задана параметрическими уравнениями
- •10. Найти точки на кривой , в которых бинормаль параллельна плоскости .
- •11. Даны параметрические уравнения кривой на плоскости
- •12. Даны параметрические уравнения двух кривых на плоскости или в пространстве, проходящих через общую точку. Определить порядок касания кривых в этой точке.
- •14. Даны параметрические уравнения кривой на плоскости или в пространстве. Записать кривую через натуральный параметр s. Выяснить длину вектора r’(s) и направление вектора r”(s).
- •16. Даны параметрические уравнения кривой на плоскости или в пространстве. Найти кривизну и кручение кривой, не переходя к натуральному параметру.
- •§ 9. Задачи для самостоятельного решения.
- •§ 10. Тестовая работа по дифференциальной геометрии кривых
- •Вариант ab.
- •§ 11. Методические указания по изучению темы дифференциальная геометрия поверхностей в трехмерном пространстве.
- •Тема 1. Способы задания поверхностей. Касательная плоскость и нормаль к поверхности.
- •Поверхность в пространстве задана одним из трех способов: параметрически, в виде графика функции или неявно. Задать ее другими оставшимися способами.
- •Поверхность в пространстве задана одним из трех способов: параметрически, в виде графика функции или неявно. Написать уравнения касательной и нормали в данной точке.
- •Тема 2. Касание поверхностей.
- •Даны параметрические уравнения поверхности. Найти какую-нибудь поверхность, имеющую с данной поверхностью в данной точке касание 1, 2, 3 порядка.
- •Даны параметрические уравнения двух поверхностей, проходящих через общую точку. Определить порядок касания поверхностей в этой точке.
- •Тема 3. Первая квадратичная форма поверхности.
- •Поверхность задана параметрически. Найти первую квадратичную форму поверхности.
- •С помощью первой квадратичной формы найти длину кривой на поверхности, угол между кривыми и площадь области на поверхности.
- •Тема 4. Вторая квадратичная форма поверхности. Полная и средняя кривизны поверхности.
- •Тема 5. Первая и вторая квадратичные формы поверхности. Гауссова и средняя кривизны поверхности.
- •§ 12. Содержание курса Дифференциальная геометрия
- •2. Теория кривых в евклидовом пространстве
- •3. Теория поверхностей в евклидовом пространстве
- •Литература
10. Найти точки на кривой , в которых бинормаль параллельна плоскости .
Решение.
Радиус-вектор
кривой
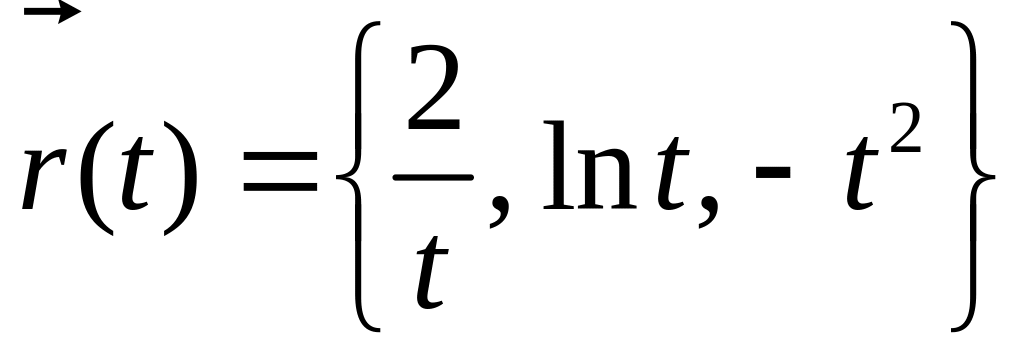 .
.
Касательный
вектор кривой (вектор скорости)
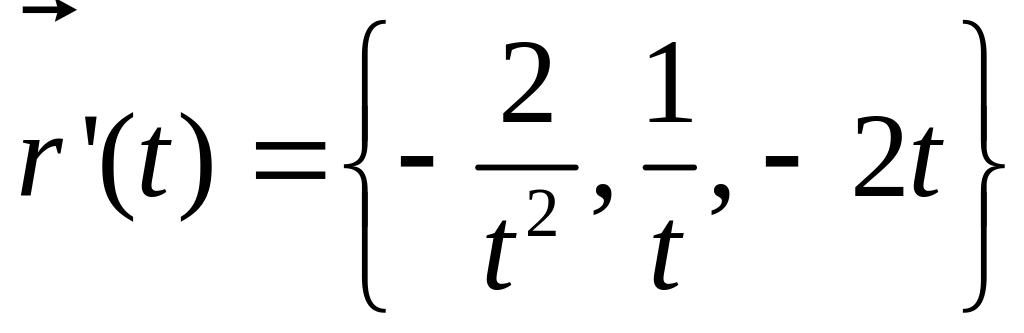 .
.
Вектор
ускорения кривой
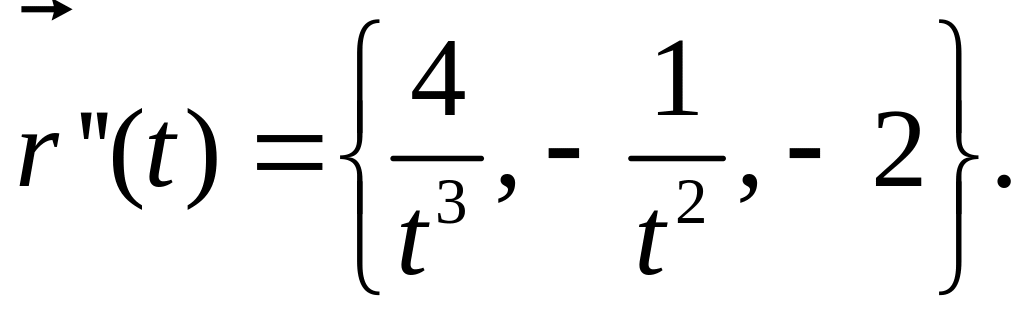
В
качестве направляющего вектора бинормали
возьмем вектор
![]() .
Его координаты
.
Его координаты
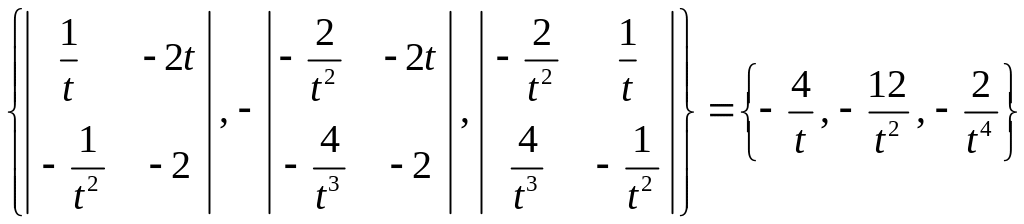 .
.
Условие
параллельности прямой с направляющим
вектором
и плоскости
![]() есть
есть
![]() .
В нашем случае имеем
.
В нашем случае имеем
![]() ,
или
,
или
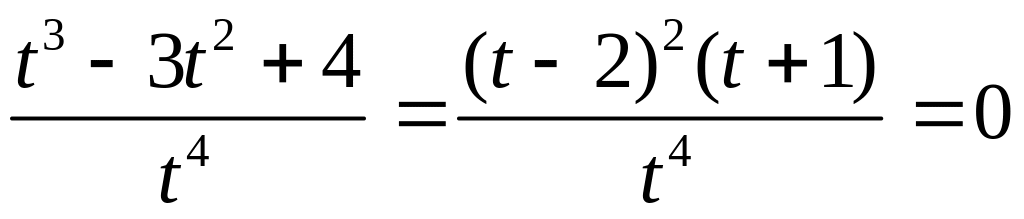 .
.
Получаем
![]() или
или
![]() .
.
При значении параметра кривая не определена.
При
точка кривой имеет координаты
![]() .
.
11. Даны параметрические уравнения кривой на плоскости
![]() .
.
Найти
какую-нибудь кривую, имеющую с данной
кривой в данной точке
![]() касание 1, 2, 3 порядка.
касание 1, 2, 3 порядка.
Решение.
Рассмотрим
всевозможные кривые, имеющие с данной
кривой
в точке
![]() касание 1-го порядка. Если задать такие
кривые в окрестности точки
параметрически с помощью натурального
параметра, то их разложение в ряд Тейлора
в окрестности точки
имеет одинаковые члены нулевого и
первого порядка. Следовательно, все
такие кривые имеют общую касательную
в окрестности точки
.
В частности, такой кривой является сама
касательная. Теперь рассмотрим
всевозможные кривые, имеющие с данной
кривой
в точке
касание 2-го порядка. Их разложение в
ряд Тейлора в окрестности точки
имеет одинаковые члены до второго
порядка включительно. В частности, если
кривая
задана параметрически
касание 1-го порядка. Если задать такие
кривые в окрестности точки
параметрически с помощью натурального
параметра, то их разложение в ряд Тейлора
в окрестности точки
имеет одинаковые члены нулевого и
первого порядка. Следовательно, все
такие кривые имеют общую касательную
в окрестности точки
.
В частности, такой кривой является сама
касательная. Теперь рассмотрим
всевозможные кривые, имеющие с данной
кривой
в точке
касание 2-го порядка. Их разложение в
ряд Тейлора в окрестности точки
имеет одинаковые члены до второго
порядка включительно. В частности, если
кривая
задана параметрически
![]() ,
то, не переходя к натуральному параметру,
можно сказать, что, например, искомой
кривой является кривая
,
то, не переходя к натуральному параметру,
можно сказать, что, например, искомой
кривой является кривая
![]() ,
где
,
где
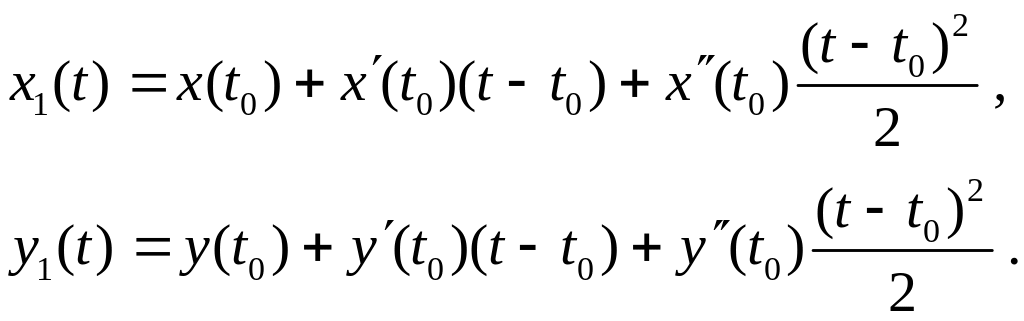
В
качестве
![]() и
и
![]() мы взяли в точности первые три члена в
разложении Тейлора для функций
мы взяли в точности первые три члена в
разложении Тейлора для функций
![]() ,
,
![]() в окрестности точки
в окрестности точки
![]() .
.
Разложим в ряд Тейлора функции , . Нам достаточно первых трех членов разложения.
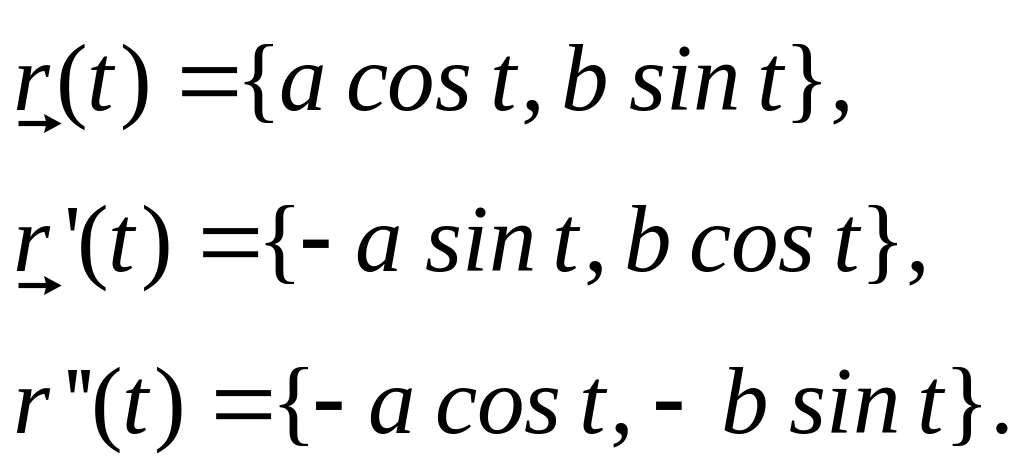
При имеем:
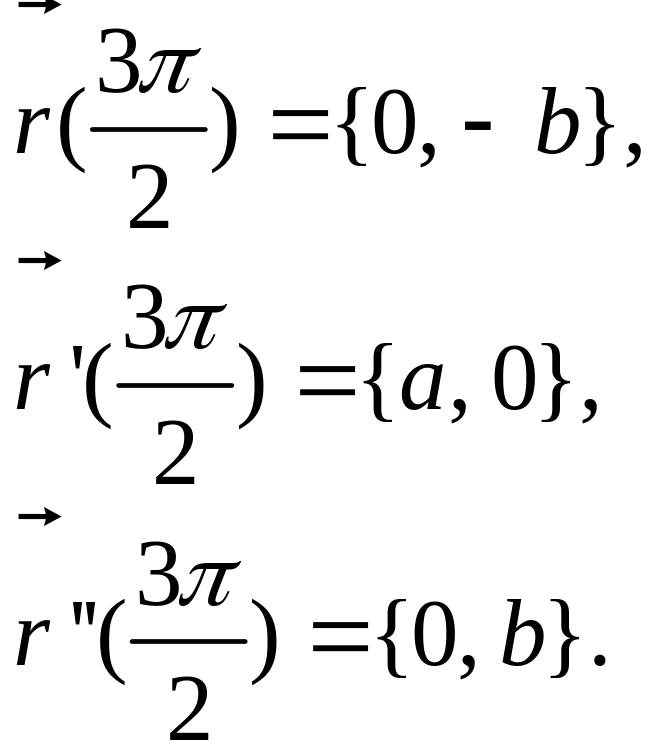
Следовательно, для
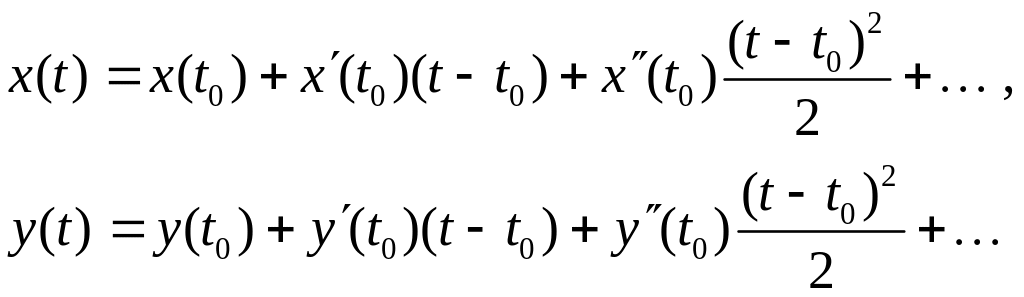
имеем:
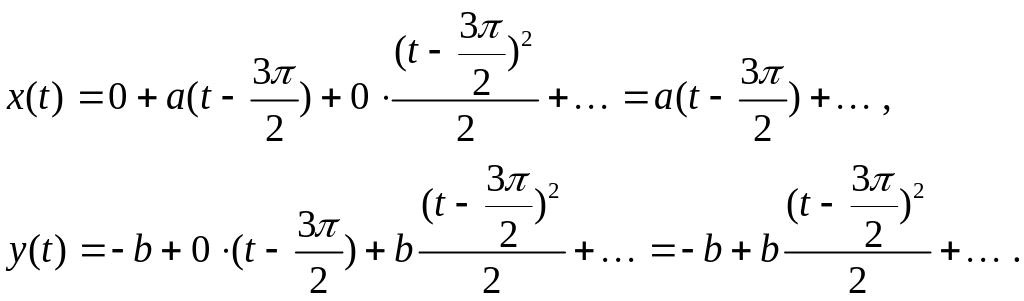
Рассмотрим
кривую
![]() :
:
 .
В точке
.
В точке
![]() она имеет с кривой
касание 2-го порядка.
она имеет с кривой
касание 2-го порядка.
Задание. Покажите, что кривая является параболой.
12. Даны параметрические уравнения двух кривых на плоскости или в пространстве, проходящих через общую точку. Определить порядок касания кривых в этой точке.
Решение.
Записать кривые через натуральный параметр.
Разложить радиус-векторы кривых в ряд в окрестности общей точки и сравнить члены этих рядов.
13. Даны параметрические уравнения кривой на плоскости или в пространстве. Найти длину кривой от одного значения параметра до другого. Нахождение значений параметров может быть самостоятельной дополнительной задачей.
а)
Найти длину астроиды
![]() .
.
Решение.
Длина
кривой от значения параметра
![]() до
до
![]() вычисляется по
формуле
вычисляется по
формуле
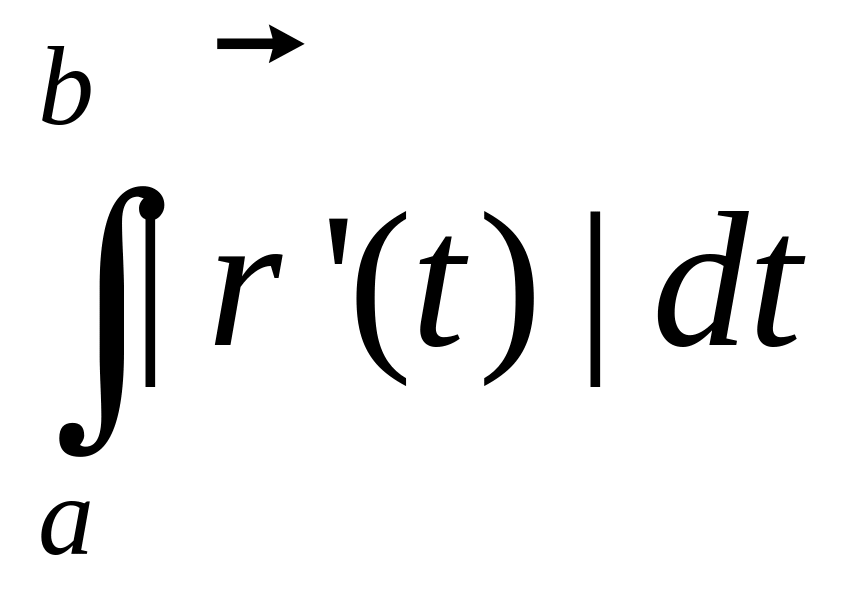 ,
где
,
где
![]() – радиус-вектор кривой.
– радиус-вектор кривой.
В случае астроиды
![]() ,
,
![]() .
.
Длина касательного вектора
![]() .
.
Астроида симметрична относительно осей координат, следовательно,
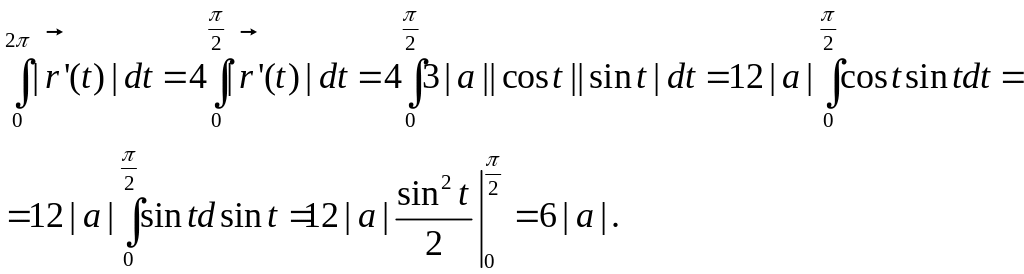
б) Найти длину дуги винтовой линии
![]() ,
,
от
точки пересечения с плоскостью
![]() до произвольной точки кривой.
до произвольной точки кривой.
Решение.
При
пересечении с плоскостью
![]() координата
координата
![]() ,
следовательно,
.
,
следовательно,
.
Касательный
вектор к кривой
![]() .
.
Длина кривой от точки пересечения с плоскостью до любой точки кривой равна
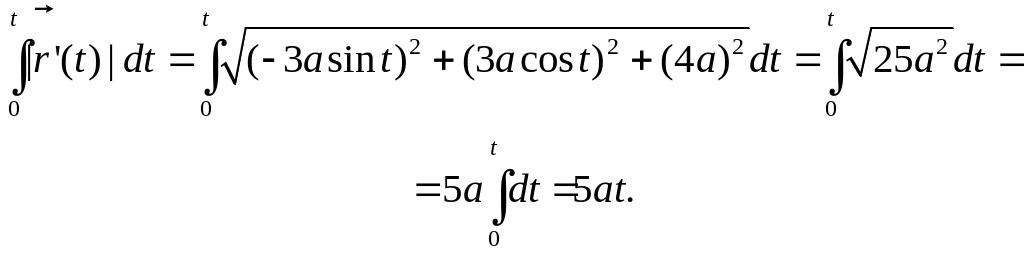
в) Найти длину замкнутой кривой
![]() .
.
Решение.
Касательный вектор к кривой
![]() .
.
Его длина равна
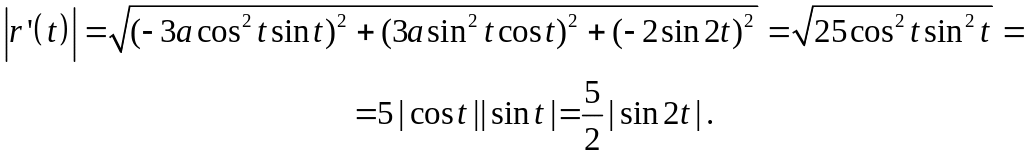
Находим длину замкнутой кривой
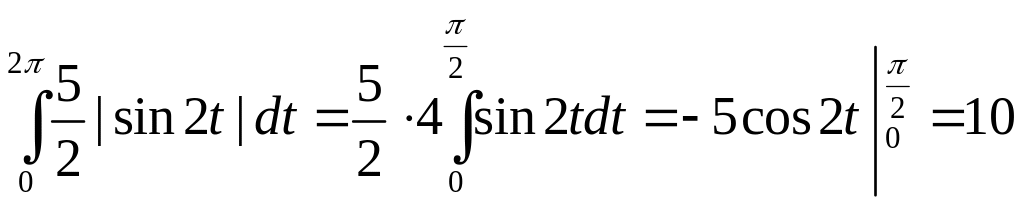 .
.
г) Найти длину дуги кривой, заданной как пересечение двух плоскостей
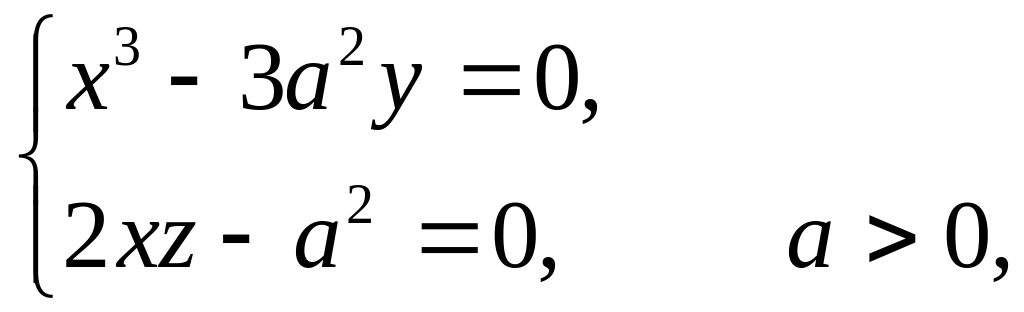
между
плоскостями
![]() и
и
![]() .
.
Решение.
Зададим
кривую параметрически, выбрав за параметр
![]() координату
координату
![]() :
:
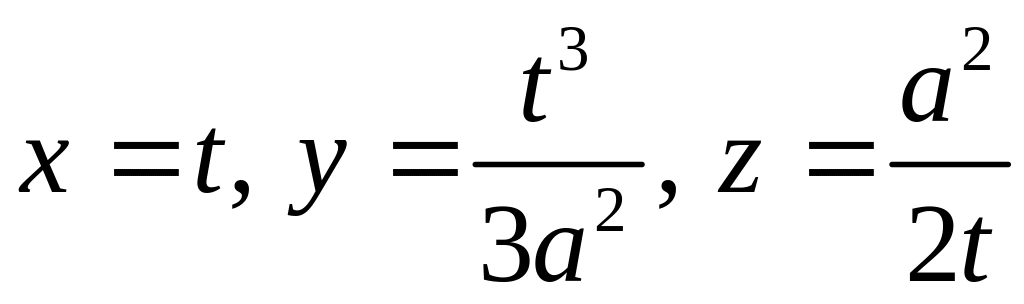 .
.
Выясним,
чему равно значение параметра
при пересечении кривой с плоскостями
и
.
Из
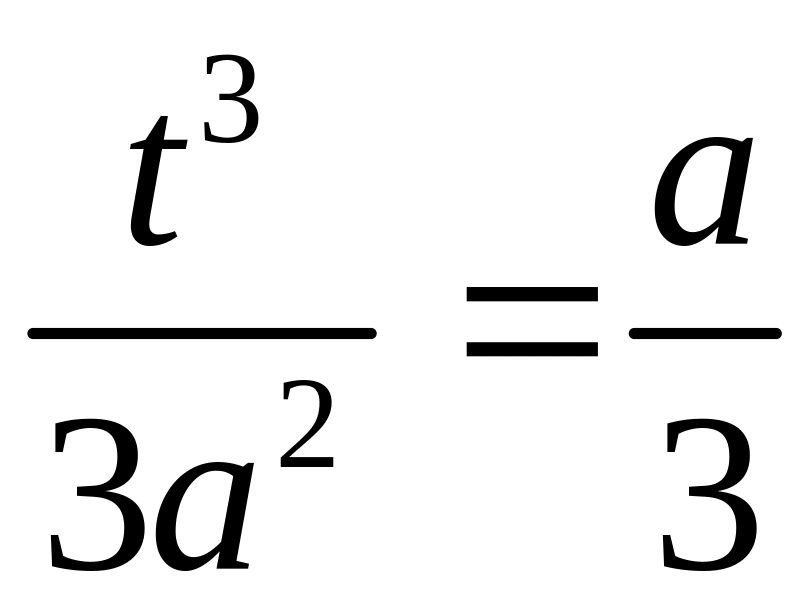 следует
,
из
следует
,
из
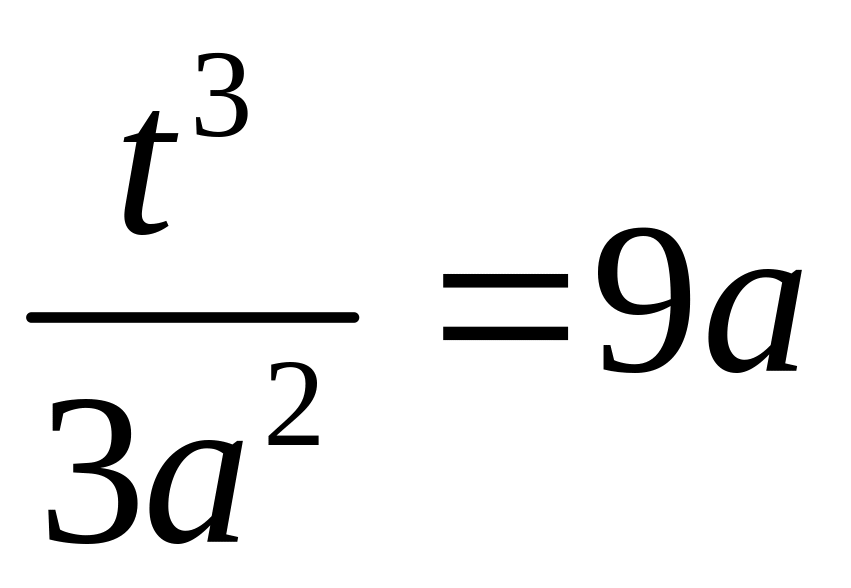 следует
следует
![]() .
.
Касательный
вектор к кривой
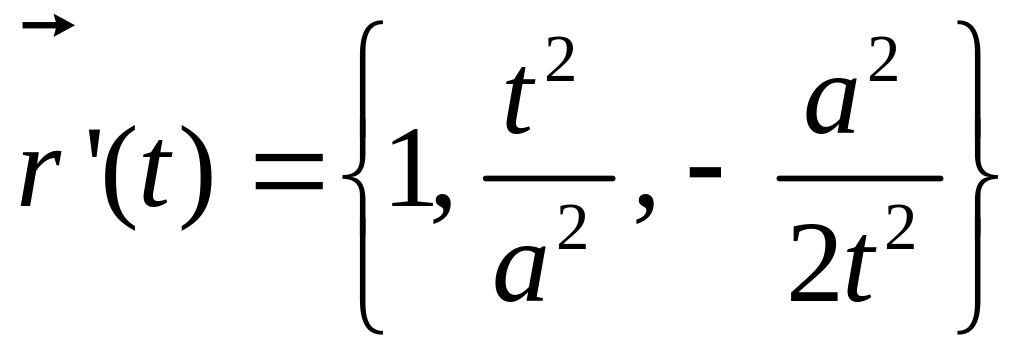 .
.
Искомая длина кривой
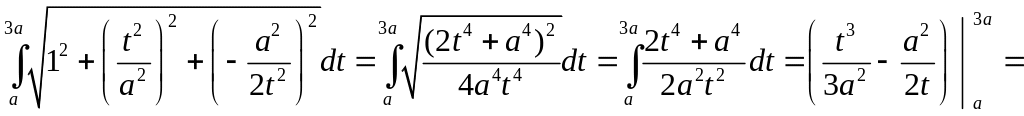
=9а.
