3.9. Резервовані системи

Відмова резервованої системи відбувається при відмові всіх елементів системи. Структурна схема надійності резервованої системи зображається умовно у вигляді паралельного з’єднання елементів (рис.3.8).

Відмова системи обчислюється як добуток відмов усіх елементів

. (3.27)

Оскільки , тому

. (3.28)

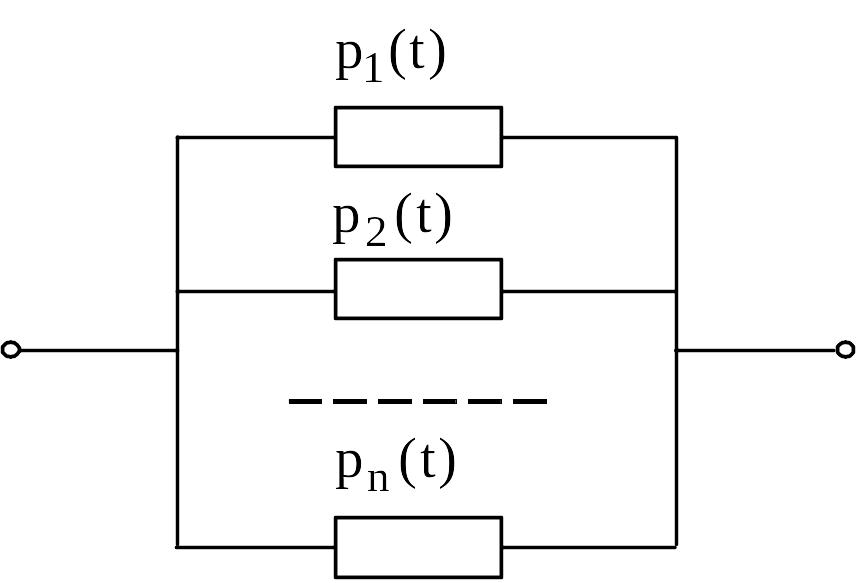
Рис. 3.8. Паралельне з’єднання елементів

Оскільки добуток при зростанні n прямує до нуля, то при збільшенні кількості елементів надійність системи зростає. При збільшенні надійності елементів p_i(t) потрібної надійності системи p_C(t) можна досягти при меншій кількості елементів паралельного з’єднання.

Якщо всі елементи мають однакову ймовірність безвідмовної роботи, то

. (3.29)

Резервування базової системи можна здійснити в різний спосіб. Можна резервувати окремі елементи, групи елементів і весь послідовний ланцюг нерезервованої системи.

Розглянемо так зване змішане резервування, коли резервуються лише найменш надійні елементи, та розглянемо задачу рівнонадійності елементів.

Приклад. Задана система надійності та ймовірність безвідмовної роботи її елементів.

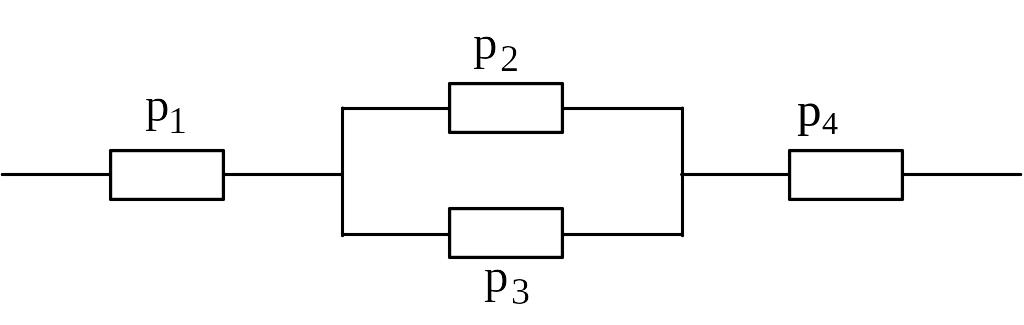
Визначимо ймовірність безвідмовної роботи системи. Спочатку розглянемо паралельне з’єднання двох елементів. Ймовірність відмови з’єднання

q_2,3 = q₂ ∙q₃ = (1 - p₂)(1 - p₃) = (1- 0,7)(1 - 0,7) = 0,09.

Ймовірність безвідмовної роботи цих двох елементів

p_2,3 = 1 – q_2,3 = 1 – 0,09 = 0,91.

Отримаємо еквівалентну схему послідовного з’єднання

Ймовірність безвідмовної роботи системи

p_c = p₁∙ p₂ ∙p₃ = 0,9 ∙0,91 ∙0,9 ≈ 0,737.

Якби не було резервування елемента 2 (відсутній елемент 3), то ймовірність безвідмовної роботи нерезервованої системи

p_cн = p₁∙ p₂ ∙p₄ = 0,9 ∙0,7 ∙0,9 ≈ 0,567.

Резервування елемента 2, що мав найменшу надійність, суттєво підвищило надійність системи. Крім того, оскільки p_2,3 = 0,91, то послідовне з’єднання з трьох елементів стало практично рівнонадійним.

Задачу рівнонадійного резервування розглянемо в такій постановці.

Нехай задано послідовне з’єднання елементів. Ймовірність безвідмовної роботи цього з’єднання p, а потрібно, щоб система мала задану (потрібну) надійність p₃. Знайдемо, скільки разів треба повторити початкову систему. Виходимо з рівняння

, , . (3.30)

Значення х округляємо до цілого числа.

3.10. Системи з релейно-контактними елементами

До цих елементів, крім релейно-контактних елементів, належать також конденсатори та випрямлячі. Особливість таких з’єднань полягає в тому, що їх елементи мають два види несумісних відмов: або обрив, або пробій, тобто мова йде про суму несумісних незалежних подій. Якщо ймовірність відмови елемента по обриву q_0i, а по пробою - q_ni, то ймовірність відмови елемента

. (3.31)

Ймовірність безвідмовної роботи елементів визначимо з рівняння

.

Звідси

. (3.32)

Розглянемо два типи конструктивного з’єднання елементів: паралельне і послідовне.

При паралельному конструктивному з’єднанні елементів (рис. 3.9) з точки зору надійності це послідовне з’єднання по пробою та паралельне з’єднання по обриву.

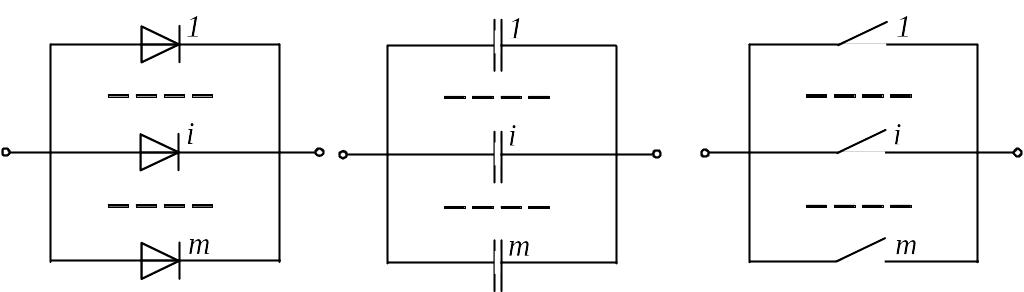
а) б) в)

Рис. 3.9. Конструктивно паралельне з’єднання:

а) випрямлячі; б) конденсатори; в) перемикачі

Схема надійності системи зображена на рис. 3.10. Вона має більш складну структуру, яка містить m елементів послідовного з’єднання з відмовами по пробою та m паралельно з’єднаних елементів з відмовами по обриву. Обидві структури з m елементів утворюють послідовне з’єднання, бо вся система відмовить, коли відмовить вся система по пробою або по обриву.

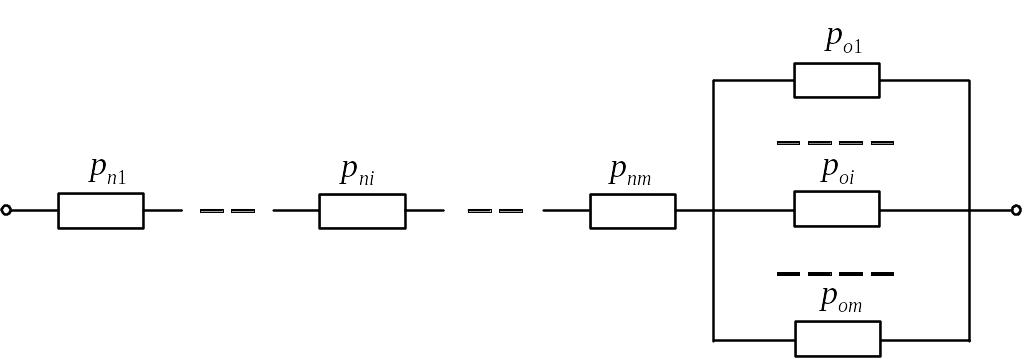
Рис. 3.10. Структурна модель надійності паралельного з’єднання

Ймовірність безвідмовної роботи з’єднання по пробою

.

Ймовірність безвідмовної роботи з’єднання по обриву

.

Оскільки , тому ймовірність безвідмовної роботи системи визначається формулою

. (3.33)

При паралельному конструктивному з’єднанні релейно-контактних елементів, конденсаторів або випрямлячів (рис. 3.11) з точки зору надійності маємо послідовне з’єднання по обриву та паралельне з’єднання по пробою

а) б) в)

Рис. 3.11. Конструктивно послідовне з’єднання:

а) випрямлячі; б) конденсатори; в) перемикачі

Схема надійності системи зображена на рис. 3.12. Тепер вже m елементів утворюють послідовне з’єднання по обриву і паралельне по пробою

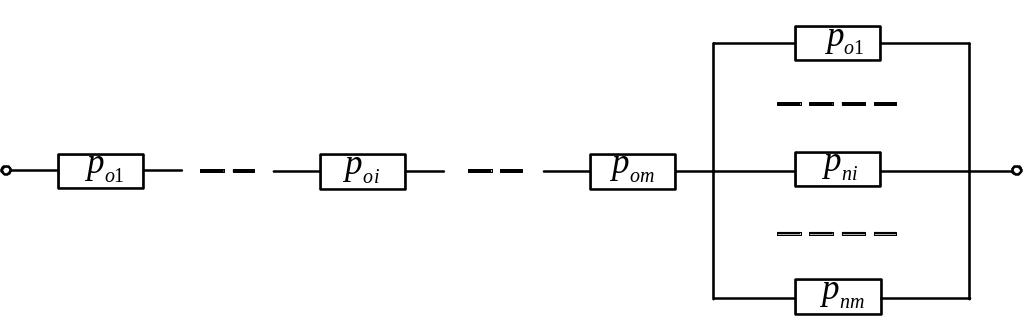
Рис. 3.12. Структурна модель надійності послідовного з’єднання

Щоб одержати формулу визначення ймовірності безвідмовної роботи такої системи, достатньо у формулі (3.33) індекси по обриву та по пробою поміняти місцями. Одержимо

. (3.34)