3.4. Інтенсивність відмов

Функції q(t) та p(t) визначаються як безумовні ймовірності. Велике практичне значення має особлива умовна ймовірність q(τ/ t), яку визначимо як ймовірність відмови на інтервалі [t, t+τ] за умови, що він йде за інтервалом [0,t] безвідмовної роботи. Тобто мова йде лише про ті вироби генеральної сукупності, що працюють на час t, виключаючи ті, що на цей час відмовили.

Розглянемо події А і В (рис.3.4):

- Подія А: ξ≤t+τ, тобто відмова відбудеться на інтервалі [0, t+τ];

- Подія В: ξ>t, тобто відмова відбувається після t.

Тоді добутком цих подій буде подія АВ: t < ξ ≤ t+τ, тобто АВ означає, що відмова відбудеться на інтервалі [t, t+τ].

Рис. 3.4. Відмови як події

Умовна відмова q(τ/t) = P(A/B).

Треба звернути увагу, що йдеться про умовну ймовірність відмови , тобто про ймовірність події А за умови, що має місце подія В

=

. (3.7)

Таким чином, одержимо

. (3.8)

Розглянемо границю відношення, яка є диференціальною ймовірністю відмови в момент t при за умови безвідмовної роботи

. (3.9)

Враховуючи (3.7), одержимо

.

Отже, інтенсивність відмов виражається через p(t) та q(t) наступним чином:

. (3.10)

З (3.10) послідовно одержуємо

; .

Сталу інтегрування C визначимо з початкової умови p(0)=1. Отримаємо . Таким чином,

. (3.11)

Функцію інтенсивності відмов λ(t) ще називають функцією відмов. У силу ряду своїх властивостей вона має велике практичне значення. Згідно з (3.10), для всіх додатних значень t вона невід’ємна, бо f(t)>0 і p(t)>0. При маємо невизначеність типу . Застосовуючи правило Лопіталя, отримаємо

, .

Згідно з (3.10) та (3.11), між λ(t) та p(t) існує взаємно однозначна відповідність. Це дозволяє функцію відмов λ(t) тлумачити як диференціальну характеристику безвідмовної роботи. Слід знати, що функція λ(t) ненормована, бо

.

Проте на обмежених інтервалах часу функція λ(t) може служити добрим наближенням функції p(t). Використання функції λ(t) має ряд практичних зручностей. Найголовнішою є та, що, зважаючи на (3.9), значення λ(t) легко одержати експериментально, а потім аналітичним шляхом, згідно (3.11), (3.3) та (3.4), знайти p(t), q(t) та f(t).

3.5. Середнє напрацювання на відмову та дисперсія безвідмовної роботи

Для розв’язку багатьох задач замість найбільш повних імовірнісних функцій p(t), q(t) чи f(t) достатньо знати кілька перших моментів випадкової величини. Нагадаємо, що початковий момент k-го порядку визначається з допомогою невласного інтеграла

.

Цей інтеграл не завжди існує. Чим більше значення k, тим менше шансів, що інтеграл сходиться. Але якщо існує момент k-го порядку, то обов’язково існують всі моменти порядку r<k. Особливе практичне значення має момент першого порядку.

Початковий момент першого порядку або математичне сподівання напрацювання системи до першої відмови позначають символом Т_в і називають напрацюванням на відмову

. (3.12)

Інтегруючи (3.12) по частинах та використовуючи, що f(t)=-p^/(t) та умови p(0)=1, p(∞)=0, одержимо:

. (3.13)

Числове значення Т_в пропорційне площі під кривою (рис. 3.5):

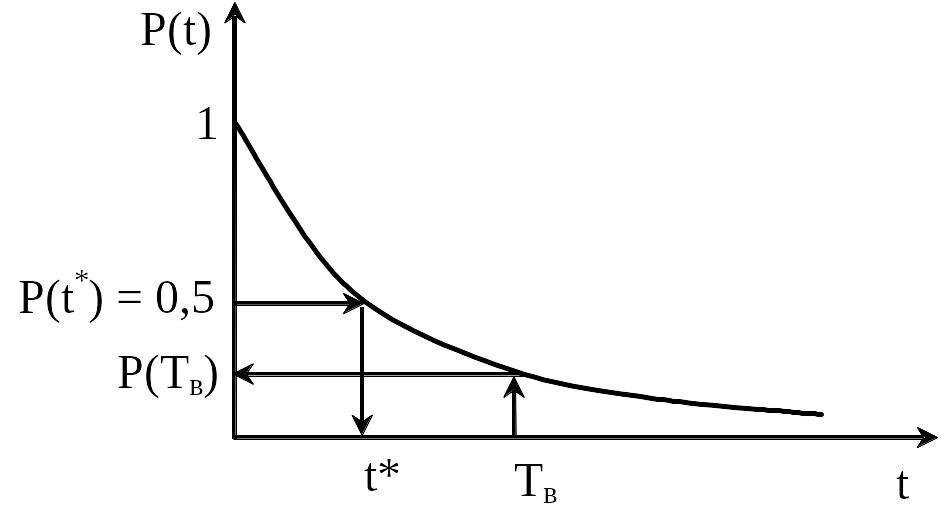
Рис. 3.5. Зв’язок між Т_в та P(Т_в)

Значення Т_в відкладемо на осі t. Введемо значення t*, при якому p(t*)=0,5. Як правило, у сучасних системах Т_в>t*, тобто p(Т_в)<0,5. Це говорить про те, що в середньому відмовляють такі системи, що достатньо виробили свій ресурс.

Для оцінки розкиду часу відмов як випадкової величини служить момент другого порядку, який є дисперсією безвідмовної роботи . Зауважимо, що Т_в та σ_T одночасно є характеристиками як відмови, так і безвідмовності. З теорії ймовірностей відомо, що

.

Але зручніше користуватися формулою

. (3.14)

Знову, інтегруючи (3.14) по частинах, остаточно одержимо

. (3.15)