2.3. Багатопараметричні показники чутливості

Результати, що одержані для однопараметричної функції, узагальнимо на випадок, коли має місце вектор-функціональна залежність . Для вихідного параметра y_j отримаємо

, (2.14)

яку розкладемо в ряд Тейлора в точці , обмежившись лінійним наближенням

.

Тоді

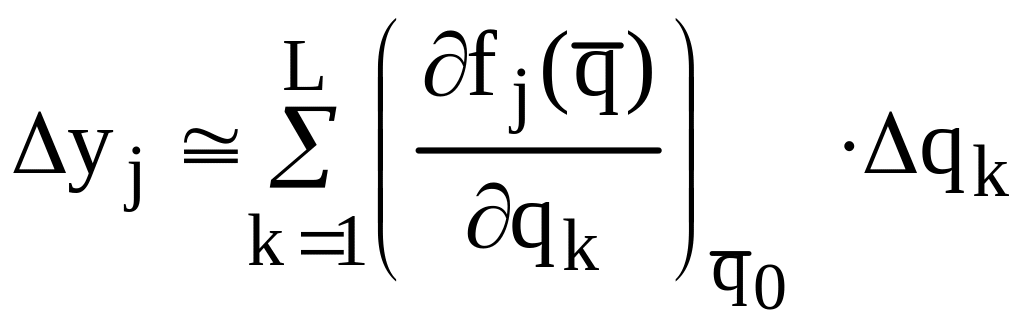, (2.15)

де , . Позначимо

. (2.16)

Рівняння (2.15) набуде вигляду

. (2.17)

Формула (2.17) дає оцінку впливу кожного абсолютного відхилення Δq_k основного параметра q_k на абсолютне відхилення Δy_j вихідної характеристики y_j.

Вектор-функцію , згідно з (2.17), можна подати в матричній формі

(2.18)

Таким чином, для загальної схеми РЕЗ (рис. 2.3) має місце залежність (2.18), яка у векторній формі набуває вигляду

, (2.19)

де – абсолютна матриця чутливості, розмірність якої N*L.

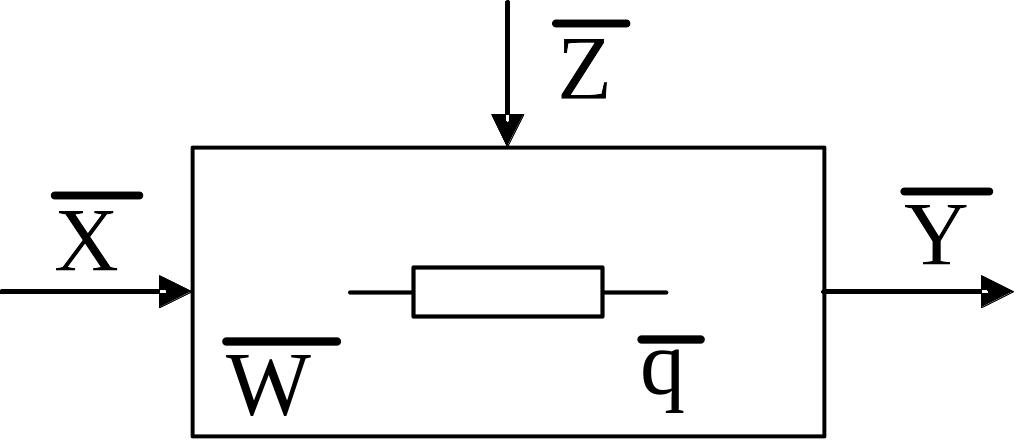
Рис. 2.3. Загальна схема РЕЗ

З (2.17) знову можемо одержати три нові модифікації формули (2.19):

, (2.20)

, (2.21)

. (2.22)

Таким чином

, , . (2.23)

У залежності від задачі, яка розв’язується, відношення має чотири форми:

,

, (2.24)

,

,

де - матриця абсолютної функції чутливості,

- матриця відносно-абсолютної функції чутливості,

- матриця абсолютно-відносної функції чутливості,

- матриця відносної функції чутливості.

У задачах системного аналізу доводиться розглядати зміну значень параметрів у широких межах. Це означає, що реальні значення можуть виявитися настільки великими, що в розкладі в ряд Тейлора у формулі (2.16) треба додатково врахувати доданки з частковими похідними вищих порядків. Але це суттєво ускладнює процедуру розрахунків. Теоретично доведено, що для досягнення необхідної точності аналізу при великих відхиленнях замість ряду Тейлора з похідними другого порядку можна користуватися простою формулою, що базується на застосуванні усередненої функції чутливості (ФЧ)

. (2.25)

Усереднена функція чутливості є середнім арифметичним двох лінійних функцій чутливості при значеннях аргументу та .

2.4. Параметрична чутливість дільника напруги

Як приклад аналізу параметричної чутливості розглянемо дільник напруги (рис. 2.4). Відомі номінальні значення опорів R₁, R₂, R₃ та вхідної напруги U. На виходах знімаються напруги U₁ і U₂. Знайти матриці абсолютної чутливості та відносної чутливості ; визначити абсолютні похибки ΔU₁ і ΔU₂ та відносні похибки ε_U1 і ε_U2 вихідних напруг.

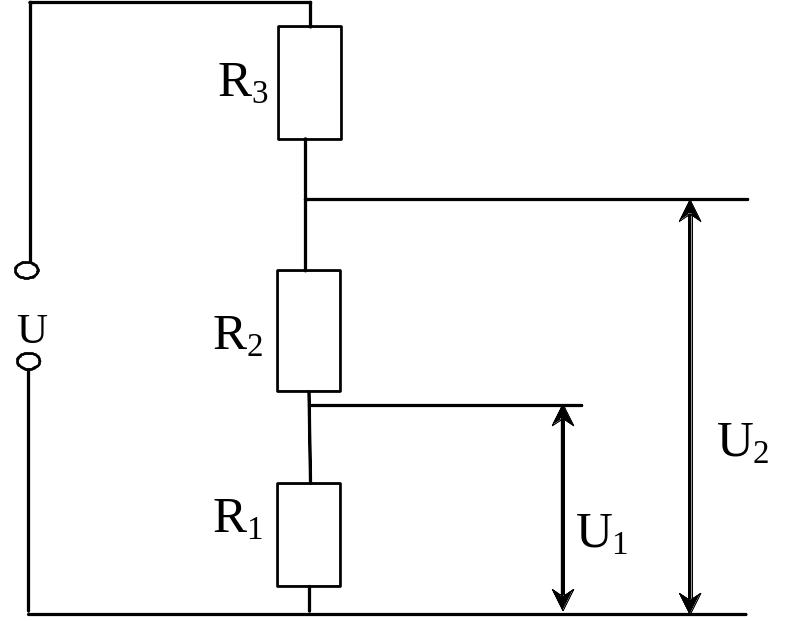
Рис. 2.4. Дільник напруги

Вектор-функція дільника напруг у матричній формі має вигляд

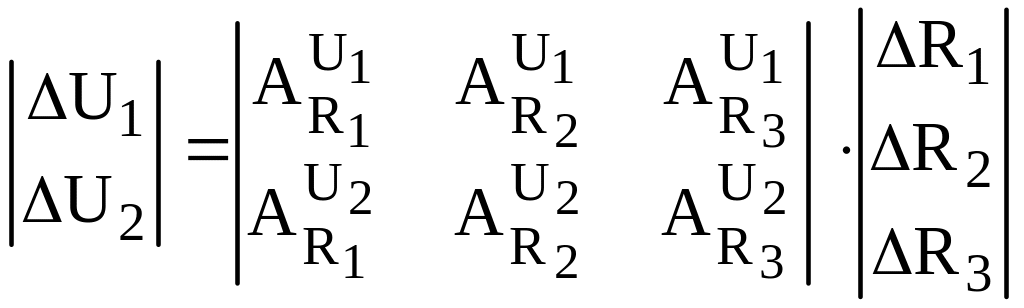
Для визначення коефіцієнтів матриці чутливості знайдемо спочатку функції U₁ = U₁ (U; R₁; R₂; R₃) та U₂ = U₂ (U; R₁; R₂; R₃). Через послідовне з’єднання опорів протікає струм

.

Звідси розрахункові значення вихідних напруг

, .

Абсолютні відхилення ΔR₁, ΔR₂ та ΔR₃ опорів від номінальних значень викличуть відповідні абсолютні відхилення ΔU₁ і ΔU₂ вихідних напруг. При цьому вважаємо, що U=const. Для визначення коефіцієнтів використовуємо формулу :

= ,

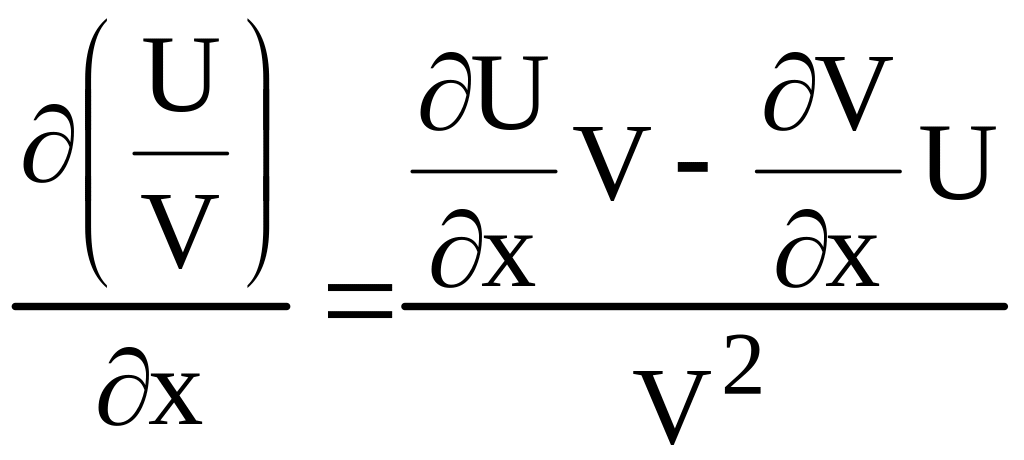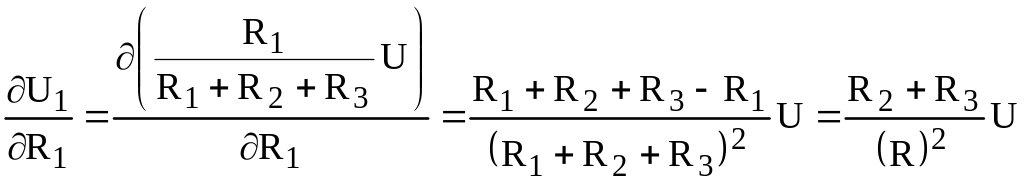де R = R₁ + R₂ + R₃.

= , = ,

= ,

= , = .

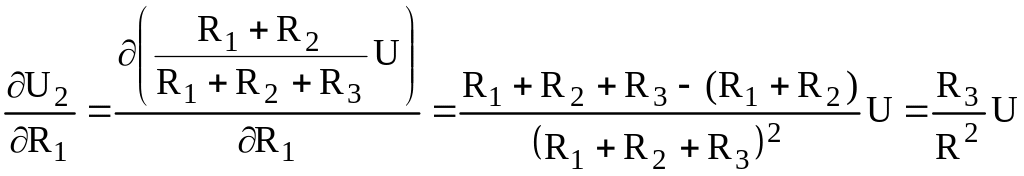Абсолютні відхилення вихідних напруг

.

.

Оскільки коефіцієнти відносної матриці чутливості , то у випадку, коли відомі відносні похибки ε_R1, ε_R2 та ε_R3, знайдемо відносні похибки вихідних напруг

.

.