18. Параметрическое и каноническое уравнение прямой.

M₀(x₀,y₀,z₀)  l

(m,n,p) – напрявляющий вектор прямой. S||l

M(x,y,z)  l

M₀M(x-x₀,y-y₀,z-z_o)

||M₀M =>

M₀M = t, tR – параметр

x – x₀ = mt x = x₀ + mt

y – y₀ = nt y = y₀ + nt (1) – пар ур-е прям

 z – z₀ = pt z = z₀ + pt

Каноническое ур-е. Из (1) выражаем t.

t =

t =

t =

= = (2) - каноническое ур-е прямой

Уравнение прямой в пространстве, проходящей ч/з 2 заданные точки.

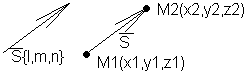
l m n

S{x₂-x₁,y₂-y₁,z₂-z₁}

19. Общее уравнение прямой в пространстве. Приведение к каноническому виду.

Прямая в пространстве рассматривается как пересечение 2х плоскостей. Поэтому:

l:  A₁x+B₁y+C₁z+D₁=0

A₂x+B₂y+C₂z+D₂=0 (4) – общие ур-я прямой

=?

M₀(x₀,y₀,z₀)  l (A₁,B₁,C₁) (A₂,B₂,C₂)

 , = =

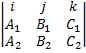
x = x₀  B₁y+C₁z =D₁- A₁x₀

B₂y+C₂z =D₂- A₂x₀

y₀, z₀ – решение системы

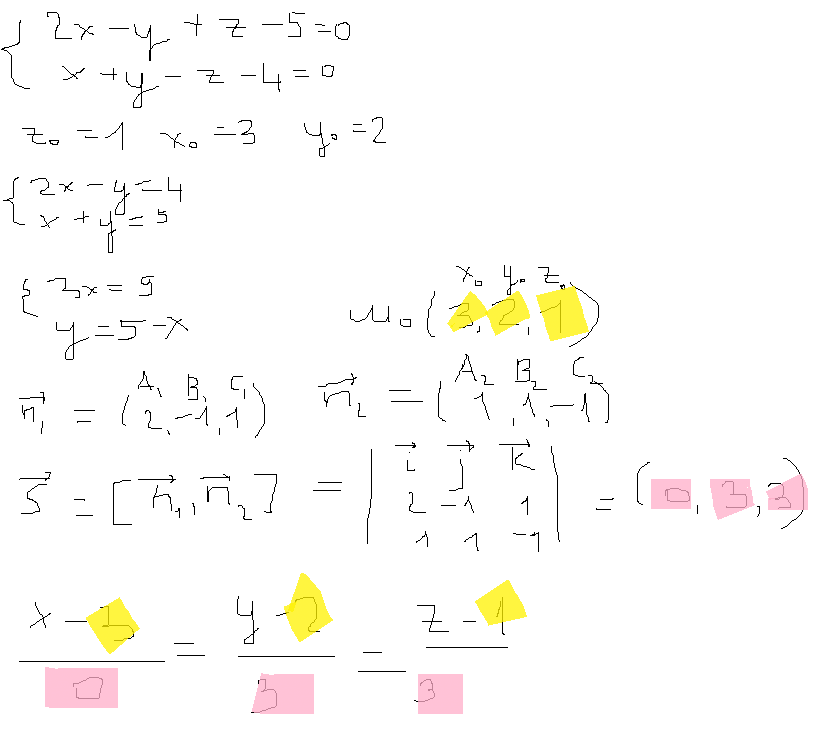
20. Расстояние от точки до прямой в пространстве.

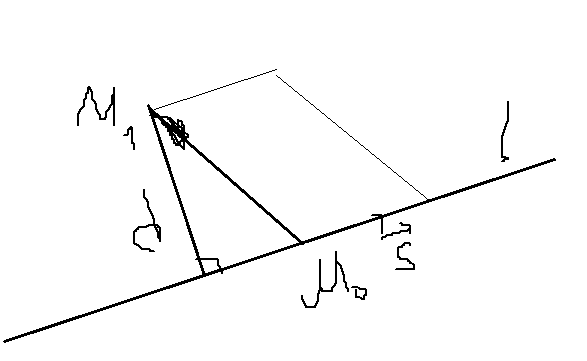
M₁(x₁,y₁,z₁₎  l

l: = =

M₀(x₀,y₀,z₀)  l

(m,n,p) – напрявляющий вектор прямой. S||l

S_{параллелограмма} = | => d = S_{параллелограмма}/ |

S_{параллелограмма} = |[ , ]|

(x₁-x₀,y₁-y₀,z₁-z_o)

d =

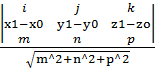
21. Угол между прямыми в пространстве. Угол между прямой и плоскостью.

Под углом между прямыми в пространстве понимают угол между прямыми, параллельными данным прямым и имеющими общую точку.

 = (l₁^l₂)

l₁: = =

l₂: = =

= (m₁, n₁, p₁) = (m₂, n₂, p₂)

|| l₁ || l₂

 = ( ^ )

cos =

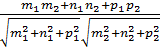
Угол между прямой и плоскостью.

l: = =

: Ax + By + Cz + D = 0

= (m, n, p) ||l

(A,B,C)  

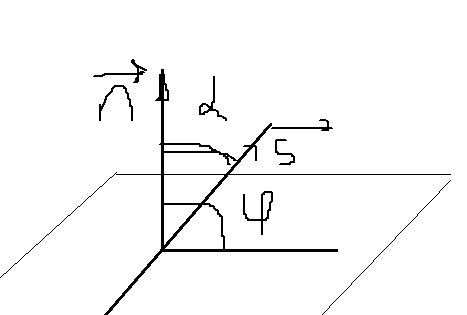
sin = cos = =

23. Общее уравнение прямой на плоскости

Сначала запишем ур-е прямой, проходящей через заданную точку  заданному вектору.

M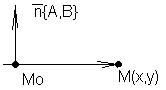 ₀(x₀,y₀)

M₀M{x-x₀,y-y₀}

n*M₀M=0

A(x-x₀)+B(y-y₀)=0

Ax+By-Ax₀-By₀=0

-Ax₀-By₀=C

Ax+By+C=0-общее уравнение прямой на плоскости.

23. Уравнение прямой в отрезках и с угловым коэффициентом.

y-y₁=k₁(x-x₁)

y=k₁x-k₁x₁+y₁

y₁-k₁x₁=b

y=k₁x+b ур-е прямой с угловым коэффициентом k.

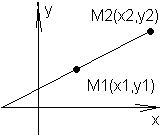
П усть даны 2 точки M₁(x₁,y₁), M₂(x₂,y₂) и x₁x₂, y₁y₂. Для составления уравнения прямой М₁М₂ запишем уравнения пучка прямых, проходящих через точку М₁: y-y₁=k(x-x₁). Т.к. М₂лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М₂ в уравнение пучка М₁: y-y₁=k(x-x₁) и найдем k:

Теперь вид искомой прямой имеет вид:

или: - Ур-е прямой, проходящей ч/з 2

25. Расстояние от точки до прямой на плоскости.

A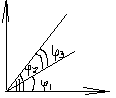 x+By+C=0, M₀(x₀,y₀)

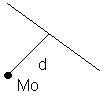
26. Угол между прямыми на плоскости.

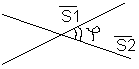
S₁{l₁,m₁}

S₂{l₂,m₂},