8. Векторы. Линейные операции над векторами.

Величины, хар-ся числовыми значениями и направлениями, называются векторными или векторами.

Геометрический вектор – направленный отрезок, кот определяется упорядоченной парой точек (А,В), где А – начало, В – конец вектора .

А В

Любая прямая, параллельная вектору, называется линией действия этого вектора.

Вектор - нулевой вектор = . У него нет направления.

Длиной или модулем вектора называется число, обозначаемое | |, равное длине отрезка АВ. Длина нулевого вектора | |= 0.

Два вектора, линии действия которых параллельны, называются коллинеарными или параллельными.

Два вектора называются равными, если:

1. Они параллельными

2. Сонаправлены

3. Имеют одинаковые длины

Любой вектор можно передвигать в пространстве параллельно самому себе, при этом он не изменяется.

Вектор, у которого не указана точка приложения, называется свободным вектором, и такие свободные вектора обозначаются , итп.

Линейные операции над векторами

1. Умножение на число.

Пусть - вектор, R – число.

Произведением вектора на число называется вектор, обозначаемый  такой, что | = ||| и  || , причем   , если >0;   если <0; 0 =

В частности, (-1) = -

2. Сложение векторов.

Пусть , – произвольные вектора.

Суммой этих векторов называется вектор, обозначаемый + , соединяющий начало вектора с концом вектора , если начало вектора помещено в конец вектора .

Определение суммы по этому правилу – правило треугольника. Суммой векторов , называется диагональ параллелограмма, построенного на этих векторах.

Разностью векторов , называется - = + (-1)

Свойства линейных операций:

1. a+b=b+a

2. (a + b) + c = a + (b + c) = a + b + c

3. α(a+b)=αa+αb

4. (α+β)a=αa+βa

5. α(βa) = β(αa) = αβa

6. a+0(вектор) = a

7. a+(-a)=0.

8. 0a=0

9. 1a=a

10. α(a + b) = αa + αb

9. Прямоугольная система координат. Направляющие косинусы вектора.

Выберем в пространстве произвольную точку О, которую будем называть началом координат. Помести базисные вектора {i,j,k} своими началами в точку О. Через начало координат и базисные векторы проводим прямые, которые называются осями координат, причем прямая, проходящая через вектор i – ось ох (ось абсцисс), через j – оу (ось ординат), через k - ось oz (ось аппликат). Конец каждого базисного вектора отмечает на оси число 1.

Пусть М – произвольная точка пространства. Вектор . Соединяющий начало координат с точкой М – радиус-вектор точки М. Вектор единственным образом разлагается по базису, т.е. существуют такие числа x,y,z что вектор = x + y + z . Координатами точки М в прямоугольной системе координат Оxyz называются координаты вектора ОМ в базисе {i,j,k}.

Для того, чтобы найчти координаты вектора, если известны координаты его начала и конца, нужно из координат конца вектора вычесть координаты его начала.

Направляющие косинусы вектора.

Пусть точка М(x,y,z); =

Пусть вектор а составляет с осями координат углы , , . Косинусы этих углов – направляющие косинусы вектора а.

Пусть вектор а (a_x,a_y,a_z)

a_x = Пр_i = | |cos

a_y = Пр_j = | |cos

a_z = Пр_k = | |cos

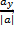• cos = cos= cos=

т.к. =

то cos =

cos =

cos =

направляющие векторы обладают след св-вами:

1. cos²+cos²+cos²=1

2. пусть (a_x,a_y,a_z) – произвольный вектор. Требуется найти ₀ , который обладает след св-вами.

₀ | ₀ |=1

₀ = ₀ = = ₀ ( , , ) => ₀ (cos, cos, cos)