3. Свойства определителей

Каждой квадратной матрице можно поставить в соответствие число, которое называется определителем, которое обозначается d(A) или = detA

1. Для матрицы A₁ = (a)

Det(a) = |a| = a

2. A₂ =

= a₁₁a₂₂ – a₁₂a₂₁

3. detA₃ = a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₂₁a₃₂a₁₃ – a₁₃a₂₂a₃₁ – a₁₂a₂₁a₃₃ – a₂₃a₃₂a₁₁

свойства определителей.

1. Det(AB) = det(A)det(B)

2. detA = detA^T Определитель матрицы равен определителю транспонированной матрицы, т.е. любое верное утверждение относительно строк определителя остается верным и для столбцов

3. общий множитель любой строки (столбца) определителя можно вынести за знак определителя, т.о. если у определителя имеется нулевая строка (столбец), то он равен нулю.

4. Если у определителля поменять местами любые две строки (столбца), то он изменит знак на противоположный, т.е. если у определителя 2 одинаковых (пропорциональные) строки (столбца), то он равен нулю.

5. Если каждый элемент строки/столбца представлен в виде суммы 2ух слагаемых, то этот определитель равен сумме 2ух определителей.

6. Если к одной троке определителся прибавить любую другую строку, умноженную на любое число, то он не изменится.

4. Минор, алгебраическое дополнение, теорема лапласа.

Пусть A_mxn – произвольная матрица и 1<=k<=min(m,n), kN. Выберем произвольным образом в матрице А k строк и k столбцов. Выбранные строки и столбцы образуют квадратную матрицу М порядка k. Определитель матрицы М_k называется минором k-того порядка матрицы А.

Пусть А_n – произвольная квадратная матрица порядка n. У этой матрицы будет равна n² миноров n-1 порядка, т.к. выбрав n-1 строку и n-1 столбец, это то же самое, что выбросить одну строку и столбец. На их пересечении стоит какой-то элемент (однозначно определенный). Поэтому любой минор n-1 порядка можно получить след образом: выбрать произвольный элемент матрицы a_ij и мысленно вычеркнуть строку и столбец, в которой он стоит. Полученный минор (определитель) обозначим М_ij = detM_n-1 – минор, полученный из исходной матрицы вычеркиванием i-той строки и j-того столбца.

Пусть а_ij произвольный элемент матрицы А_n. Алгебраическим дополнением элемента а_ij называется число А_ij , определяемое по формуле

A_{ij =} (-1)^i+jM_ij

Теорема Лапласа

Определитель матрицы равен сумме попарных произведений эелементво любой строки (столбца) на их алгебраическое дополнение. Следствие: определитель треугольной матрицы равен произведению диагональных элементов. Вычисление определителя по т.Лапласа называется разложением определения по i строке (j столбцу)

5. Обратная матрица.

Понятние обратной матрицы существует только для квадратных матриц.

Определение. Пусть а – квадратная матрица. Матрицей, обратной А, называется матрица, обозначаемая А^-1, такая что АА^-1 = А^-1А = Е, где Е – единичная матрица.

Квадаратная матрица называется невырожденной, если ее определитель отличен от нуля, и вырожденной – в противном случае.

Теорема: для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Доказательство. Есть А^-1  detA0

Необходимость. У А есть А^-1

Надо доказать что detA0

Т.к. АА^-1 = Е => det(AA^-1) = detE => detAdetA^-1 = detE. Т.е. detAdetA^-1=1 =>detA0

Достаточность. Дано: detA0. Надо доказать что существует А^-1

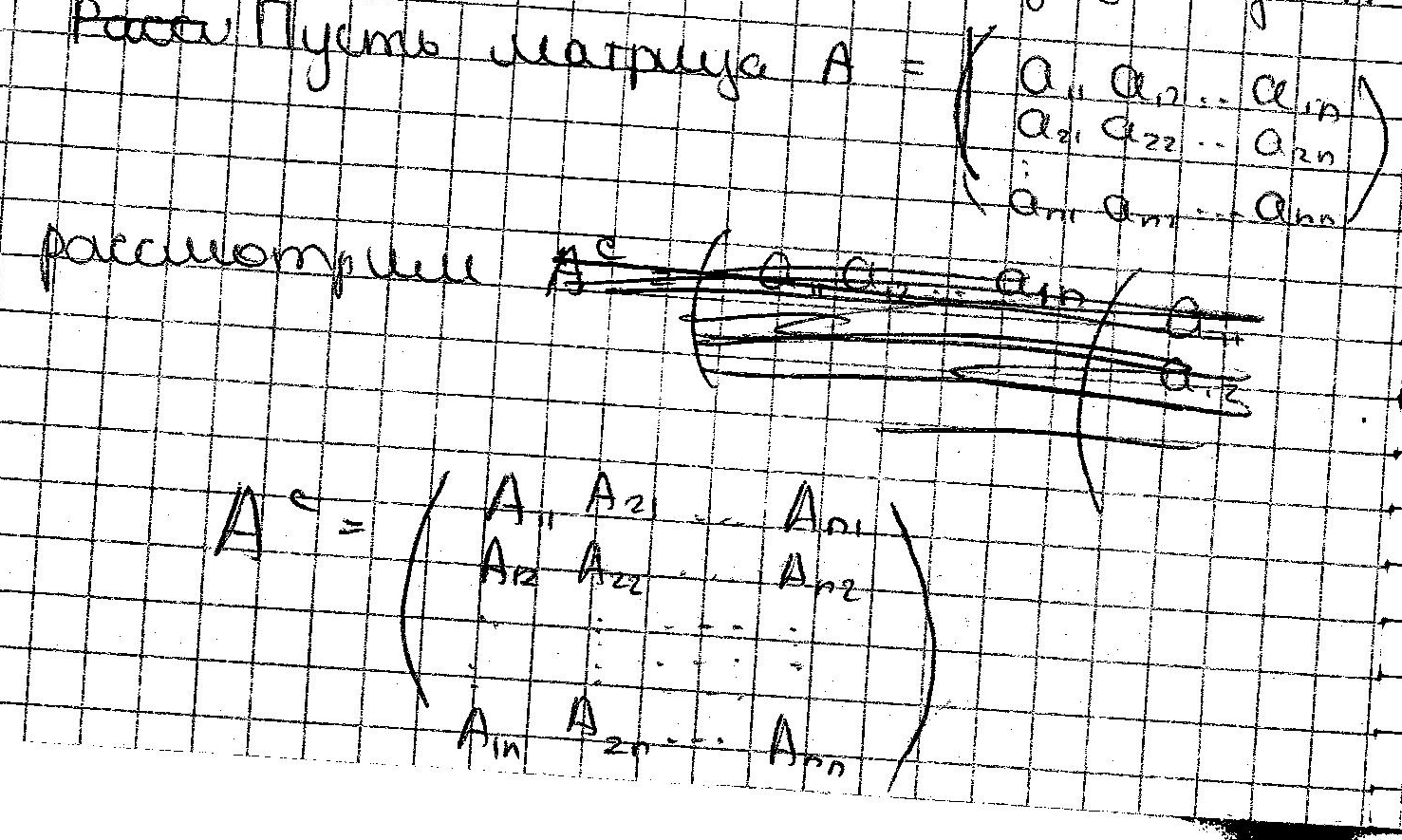
Схема построения обратной матрицы.

1. Находим detA=d0

2. Находим все алгебраические дополнения A_ij

3. Строим матрицу А^с = (A_ij)^T

4. A^-1 = (1/detA)A^c

Если обратная матрица существует, то она единственная. Действительно. A, detA0 и пусть B, C – две обратные к А.

Рассмотрим. BAC = (BA)C = EC = C => B=C

B(AC) = BE = B

Понятие обратной матрицы позволяет решать т.н. матричные ур-я вида АХ = В, где А, В – заданные матрицы, Х – неизвестная матрица.

Действительно. Если |A|0 , то есть A^-1 умножим: A^-1(AX) = A^-1B => X=A^-1B

Аналогично: XA = B, X=BA^-1

Или: AXB = C => X = A^-1CB^-1