21.Условная вероятность.Теоремы сложения и умножения вероятностей.

Опред-я классич.и геометрич.вероятностей позволяют находить в простейших случаях вероят-ти тех или иных событий непосредственно.Но часто возникает задача,в кот зная вер-ти неких простых событий,надо определить вер-ти других более сложных.В этом случ.пользуются теоремами,которые называют основными теоремами тервера.

Общая теорема сложения:Для любых событий АиВ имеет место формула

Р(А+В)=Р(А)+Р(В)-Р(АВ). Если соб-я АиВ несовместны,то Р(А+В)=Р(А)+Р(В).

Под условн вер-ю событ В при условии А понимается число Р(В/А)=m(AB)/m(A), где m(A)-кол-во элемент.событий,благоприятств.А,m(AB)-колво элем.событий, благоприят.АиВ одновременно.Это опред-е напоминает опред-е классич.вер-ти с одной сущест.разницей-исход.группа элем.событий сужена,из нее оставлены лишь те,кот.благоприятствуют А.Из этого опред-я следует Р(В/А)=Р(АВ)/Р(А).Это тоже можно принять за опред-е.

Общая теорема умножения:для люб соб-й АиВ имеет место формула

Р(АВ)=Р(А)*Р(В/А). Будем говорить что соб-е В не зависит от А,если осуществ-е А не меняет вероят-ти осущест-я соб-я В,т.е.Р(В/А)=Р(В).

М ожно сказать,что в этом случ.и соб-е А не зависит от В,поэтому говорят события АиВ независимы.Если АиВ независимы,то из общ теоремы умножения получ-ся Р(АВ)=Р(А)*Р(В)-теорема умножения для независимых событий. Полезно иметь в виду,что Р(А)=1-Р(А).

Пример:из урны,содержащей 5ч и 4б шара извлекается последовательно 2 шара. Какова вероятность того,что второй шар черный,если известно,что первый был черный?

А-{первый шар черный}, В-{второй шар черный}

тогда АВ-{оба шара черные}

Р(В/А)-?

22.Формулы полной вероятности и Байеса.

На практике часто имеем дело с процессами,кот могут развив-ся по одному из нескольких вариантов,возникает 2 задачи:

1)Найти вер-ть того,что в рез-те такого процесса произойдет некое событие А

2)Оценить,по какому из вариантов развивался процесс,если известно,что в рез-те него произошло событие А.

Первая задача реш-ся с помощью формулы полной вероятности.Вторая-с помощь формулы Байеса.При решении подобных задач следует в перв очередь правильно оценить все возможные варианты процесса или иными словами правильно выбрать группу гипотез относительно протекания процесса.

Опр:события Н1,Н2..Нn образуют группу гипотез,если они

~Образуют полную группу ~Попарно несовместны

Для группы гипотез в отлич от группы элем.событий не треб-ся равновер-ть.Если Н1..Нn группа гипотез,то для люб.соб-я Н имеет место формула полной вер-ти

Если соб.А произошло,то вер-ть осущест-я каждой из гипотез наход.по ф.Байеса:

Пример:известно,что 90% изделий,выпускаемых предприятием,отвеч стандарту. Упрощенн схема проверки кач-ва признает пригодной стандартную деталь с вер-ю 0,96 и нестрандарт с 0,06.Определить вер-ть того,что:

1)Взятое наугад изделие пройдет контроль

2)Изделие,прошедшее контроль,отвечает стандарту

90% отвечают стандарту

0,96-годна стандартная, 0,06 – годна нестрандартная

гипотезы: Н1{деталь стандартная},Н2{деталь нестандартная}

события: А{деталь пройдет контроль}

1. Р(А)-? Р(А/Н1)=0,96 Р(А/Н2)=0,06

Р(Н1)=0,9 Р(Н2)=0,1

Р(А)=Р(Н1)Р(А/Н1)+Р(Н2)Р(А/Н2)=0,9*0,96+0,1*0,06=0,87

2. Р(Н1/А)-?

23.Повторные испытания.Формула Бернулли и ее приближения(Пуассон и локальная терема Муавра-Лапласа)

Распростран.ситуация в тервере-изучение серии испыт-й,в некот.смысле явл-ся одинаковыми.Говорят,что серия испытаний удовлетв.схеме Бернулли если:

1)В кажд.испытании некот.событ.А либо осущ-ся,либо не осущ-ся.

2)Вер-ть осущ-я события А одна и та же во всех испытаниях (Р)

3)Результат каждого испыт-я не зависит от рез-та предыдущих.

Основн.задача-найти вер-ть того,что в серии из n испытаний соб-е А осуществ-сь ровно n раз.Она вычисляется по формуле Бернулли ,q=1-p.

Ф.Бернулли хотя и дает точный ответ на поставл.вопрос,но при больших знач-ях m и n станов-ся бесполезной из-за объема вычислений.Тогда исп-ся одна из предельных теорем. Если m и n достаточно велики,но величина ограничена,исп-ся локальная теорема Муавра-Лапласа.

,где ;

Значения ф-ции φ(х) находятся по таблице.

Если m велико а n мало,но величина λ=np ограничена,то используется теорема Пуассона

!если в задаче можно применить любую из двух теорем,то при npq<9 точнее Пуассон. Часто требуется найти вер-ть того,что при бльшом числе испытаний n кол-во наступлений события А заключено в нек.промежутке m1≤m≤m2. В этом случае используют интегральную теорему Муавра-Лапласа.

, где ,где Ф-функция Лапласа.

. Со схемой Бернулли связана задача:Найти наиболее вероятн. кол-во наступлений события А,т.е.среди всех m=1,2..n найти такое знач-е,для кот. вер-ть Pn(m) наибольшая.Такое знач-е m0=[p(n+1)],квадр.скобки обознач.целую часть числа.Если р(n+1) целое,то наиб.вер.явл-ся 2 значения:m0 и m0-1.

Пример:монету подбрас.10раз.Какова вер-ть того,что герб выпадет 4 раза,ни разу, хотя бы 1 раз.

1.n=10,m=4.

2.n=10,m=0.

3. 1-1/1024=0,999

24. Дискретные случ.величины и законы их распределения

Понятие случ велич-ы явл-ся основным в тервере и ее прилож-ях.Случ-и велич-и, яв-ся число выпавших очков при однократн бросании игральной кости,число распавшихся атомов радия за дан промежут времени,число вызовов на телефон станции за некотор промежуток времени.Т.о.случайн величиной наз-ся переменн величина,котор в рез-те опыта может принимать то или иное числов значение.  Опр:Говорят,что задана дискретн случ величина ξ , если указано конечное или счетное множество чисел и каждому из этих чисел xi поставлено в соответств некотор положительн число pi , причем Числа   наз-ся возможными знач-ми случайн величины   , а числа  - вероятн-ми этих значений  Если возможн знач-ия случ величины   образуют конечную последовательность x1,x2,...,xn,то закон распред-ия вероят-ей случайн величины задают в виде  дующей таблицы, в которой и

значения ξ	х1	х2	…	хn
Вер-ти p(xi)	p1	p2	…	pn

Эту таблицу назыв рядом распредел-ия случайн величины  . Наглядно функцию р(х) можно изобраз в виде графика. Для этого возьмем прямоугольную систему координат на плоскости. Получающаяся при этом ломаная линия назыв-ся многоугольником распред-ия случ величины 

Биномиальный закон распределения реализ-ся в схеме Бернулли ,где p,n,m-параметры распределения.

~Свойства:

Пусть заданы натуральные числа m, n, s, причем   Если возможными значениями дискретн случ величины   являются 0,1,2,…, m, а соответствующие им вер-ти выраж-ся по формуле

то говорят, что случайная величина ξ имеет гипергеометрический закон распределения.

Р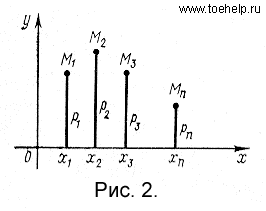 аспределение Пуассона:

Опр:дискрет случ величина Х принимающ счетное множество значений {0,1,2..}

подчин-ся закону распр Пуассона если вер-ти ее возможных значений задаются формулой где а-параметр распред-я.

~Свойства: M(x)=D(x)=a