Поле двухпроводной линии
Пусть заданы радиусы R проводов, расстояние D между геометрическими осями и приложенное к проводам напряжение. Из уравнений (h-a)(h+a)=R2; 2h=D можно определить положение электрических осей.
Потенциалы проводов φ1,2=±(τ/2πεε0)ln(h+a)/R. Напряжение U=(τ/πεε0)ln(D-(h-a)/R.
Емкость на единицу длины C0=τ/U= πεε0/ ln(D-(h-a)/R.
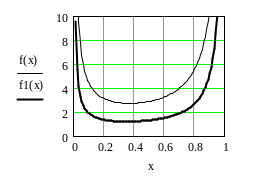
На графике представлена зависимость f(x)= Eнаиб от x=r1/r2 для кабеля и f1(x)= Eнаиб от x=R/h для двухпроводной линии.
Наибольшая напряженность поля у поверхности проводов и если ввести обозначение x=R/h, ее можно представить в виде
.
Она минимальна при x0=0,342. Это условие максимальной электрической прочности линии. При x≤0,342 (D≥5,85R) корона носит устойчивый характер.
Поле параллельных несоосных цилиндров
Решение задачи для двух заряженных осей дает возможность найти поле между двумя несоосными цилиндрами, имеющими круглые сечения различных радиусов R1 и R2. Действительно, всегда можно так расположить электрические оси, чтобы в их поле две поверхности равного потенциала совпали с поверхностями заданных проводящих цилиндров. Пусть D – расстояние между геометрическими осями цилиндров, h1 и h2 – расстояния от геометрических осей до плоскости нулевого потенциала, а – расстояние от электрических осей до этой плоскости. Тогда
(h1-a) (h1+a)=R12,
(h2-a) (h2+a)=R22,
h2±h1=D.
При расположении одного цилиндра снаружи другого в последней формуле выбирается знак «+», а одного внутри другого знак – «-». Решение системы
h1=±(D2+R12-R22)/2D; h2=(D2+R22-R12)/2D; a2=h2-R2.
Потенциалы цилиндров φ1=(τ/2πεε0)ln(h1+a)/R1; φ2=(τ/2πεε0)ln R2/(h2±a).
Напряжение U=(τ/2πεε0)ln((h1+a)(h2±a))/R1R2.
Емкость на единицу длины C0=τ/U= 2πεε0/ ln((h1+a)(h2±a))/R1R2.
Метод изображений
Метод изображений применим в тех задачах, где нужно найти поле зарядов вблизи граничных поверхностей. Можно подобрать такую систему зарядов (изображений), расположенных вне области определения поля и изменения параметров среды по другую сторону граничной поверхности так, чтобы среда стала однородной, что поле действительных зарядов и их изображений обеспечивало требуемые граничные условия. Замена задачи с граничными условиями, на эквивалентную задачу с зарядами изображениями в однородной области без граничных условий называется методом изображений.
Граничная поверхность – плоскость.
1.Граница раздела: диэлектрик – проводник. (Задача Дирихле φ=0). Каждый заряд должен быть зеркально отражен в поверхности проводящей среды с изменением знака заряда, после чего проводящая среда может быть мысленно удалена и рассмотрено поле действительных зарядов и их изображений.
2. Граница раздела: диэлектрик – диэлектрик. Условия на поверхности раздела двух диэлектриков E1t=E2t, D1n=D2n будут выполнены. Если поле первой среды будет создаваться зарядом q и его изображением q1=q(ε1 - ε2)/(ε1 + ε2) в однородной среде с диэлектрической проницаемостью ε1, А поле второй среды будет создаваться изображением заряда q2=q2ε2/(ε1+ε2) в однородной среде с диэлектрической проницаемостью ε2.
3. На граничной поверхности заданы условия Неймана ∂φ∕∂n=0. В этом случае, в отличии от задачи Дирихле, изображение не изменяет знак.
Емкость круглого цилиндра относительно плоскости
Геометрическая ось цилиндра радиуса R находится на высоте h над проводящей плоскостью (над поверхностью Земли). Между цилиндром и плоскостью напряжение U. Положение электрических осей (заряда и его изображения) можно определить из уравнения (h-a)(h+a)=R2.
Потенциал цилиндра φ=(τ/2πεε0)ln(h+a)/R.
Потенциал плоскости φ=0. Напряжение U=φ. Линейная плотность заряда τ=U2πεε0/ ln(h+a)/R.
Емкость на единицу длины C0=τ/U= 2πεε0/ ln(h+a)/R.
В случае тонкого провода, подвешенного высоко над поверхностью Земли h+a≈2h и емкость C0= 2πεε0/ ln2h/R.
Потенциальные, емкостные коэффициенты и частичные емкости
В системе нескольких заряженных тел потенциал каждого тела определяется не только зарядом данного тела, но и зарядами остальных. Если тела имеют малые размеры, то можно пренебречь искажением поля, возникающим от появления на телах индуцированных зарядов.
В общем случае, когда имеется n заряженных тел, потенциалы могут быть найдены на основе принципа наложения.
φ1=α11q1+ α12q2+…+ α1nqn;
φ2=α21q1+ α22q2+…+ α2nqn;
. . . . . . . . . . .
φn=αn1q1+ αn2q2+…+ αnnqn.
Коэффициенты α носят название потенциальных коэффициентов. Они зависят от формы и размеров поверхностей тел, от взаимного расположения тел и от диэлектрической проницаемости среды. Коэффициенты αkk с одинаковыми индексами называются собственными потенциальными коэффициентами, а коэффициенты αkn c разными индексами – взаимными потенциальными коэффициентами. Эти уравнения служат для вычисления потенциалов тел по заданным их зарядам. [α]=1/Ф.
При возникновении обратной задачи, решая приведенные уравнения относительно зарядов, можно получить
q1=β11φ1+ β12φ2+…+ β1nφn;
q2=β21φ1+ β22φ2+…+ β2nφn;
. . . . . . . . . . .
qn=βn1φ1+ βn2φ2+…+ βnnφn.
Коэффициенты β называются емкостными (или коэффициентами электростатической индукции) – собственными при одинаковых индексах и взаимными при разных индексах. [β]=Ф.
Для определения опытным путем коэффициента βkk cледует, заземлив все тела, кроме k-ого, сообщить последнему потенциал φk, отключить вольтметр и источник и разрядить на землю через баллистический гальванометр. По отбросу гальванометра определить заряд тела и вычислить собственный емкостный коэффициент. Если в том же опыте измерить заряд другого тела, то появится возможность определить и взаимный коэффициент. Взаимные емкостные коэффициенты отрицательны.
Часто заряды тел выражают через разности потенциалов данного тела и других тел, в том числе и земли.
q1=С11 (φ1-0)+ С12(φ1 -φ2)+…+ С1n ( φ1 -φn);
q2=С21 (φ2 -φ1)+ С22 (φ2-0)+…+ С2n (φ2 -φn);
. . . . . . . . . . .
qn=Сn1 (φn -φ1)+ Сn2 (φn -φ2)+…+ Сnn (φn -0).
Коэффициенты С в этих уравнениях называются частичными емкостями – собственными при одинаковых индексах и взаимными при различных индексах. При этом Скк=βк1+ βк2+…+ βкn; Скp=- βкp.