#11 Точки разрыва и их классификация

Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке.

Устранимый разрыв - если предел в этой точке существует, но в т. х=а, f(x) или не определено, или частное значение f(a) не равно предельному значению.

Разрыв первого рода - т. а,..., если значение f(x) имеет конечный, но не равный друг-другу левые и правые предельные значения.

Разрыв второго рода - если один из односторонних пределов не сущ. или уходит на бесконечность

#12 Производная числа (x₀) наз-ся число f’(x₀)=lim(x0)(f(x₀+x)-f(x₀))/ x

{Предел отношения приращения ф-ии к приращению аргумента, бла бла бла}

Геометрический смысл: производная в точке равняется tg угла наклона касательной, проведенной к графику функции в этой точке.

Механический смысл: Пусть s = s(t) — закон прямолинейного движения. Тогда v(t₀) = s'(t₀) выражает мгновенную скорость движения в момент времени t₀. Вторая производная a(t₀) = s''(t₀) выражает мгновенное ускорение в момент времени t₀. Вообще производная функции y = f(x) в точке x₀ выражает скорость изменения функции в точке x₀, то есть скорость протекания процесса, описанного зависимостью y = f(x).

#13 Связь непрер-ности и дифференцируемости

Т-ма. Для того, чтобы ф-ия y=f(x) была непрерывна в точке x0, необходимо и достаточно, чтобы в окрестности этой точки бесконечно малому приращению аргумента x0 соотв. бесконечно малое приращение y

Док-во: 1) f(x) в окр. a.; xa; f(x) f(a), но x=a+x, следовательно f=f(a+x)-f(a), сделовательно f0

2)если x0, то f0, следовательно lim(xа)(f(а+x)=f(а), следовательно f(x) непрерывна в т. x=a

Опред. y=f(x) явл. дифференц., если в т-ке x0 ее приращение можно представить в виде y=A*x+o(x)*x, где A=const, lim(x0)(o(x))=0;

Т-ма. Чтобы ф-ия была дифференц., необходимо, чтобы она имела в данной точке конечную производную

Док-во.1)Если y=f(x)-диффер,y/x =A +o(x),

Перейдем к пределу, y'= lim(x0)( y/x)=A

2) Пусть существует конечная производная, тогда существует конечный предел lim(x0)( y/x)=y', получаем o(x)=y' - y/x.

Т-ма (дифференцируемость и непрерывность). Если  функция дифференцируема в точке x, то она непрерывна в этой точке.

Док-во: Так как функция дифференцируема в точке x, то то ее приращение представимо в виде,y/x =A +o(x), из которого следует, что предел lim(x0)( y)=0, , что означает непрерывность функции в данной точке.

#14 Арифм. действия с производными

 

а) 

б) 

Док-во: 1)Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).

Тогда

Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.

Следовательно,

.

2)Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому

Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).

Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.

Поэтому можем записать

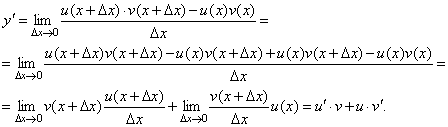
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.

Пусть, например, y=u·v·w. Тогда,

y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '.

3)Пусть  . Тогда

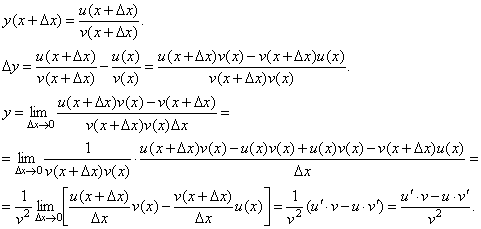
При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.

#15 Таблица производных

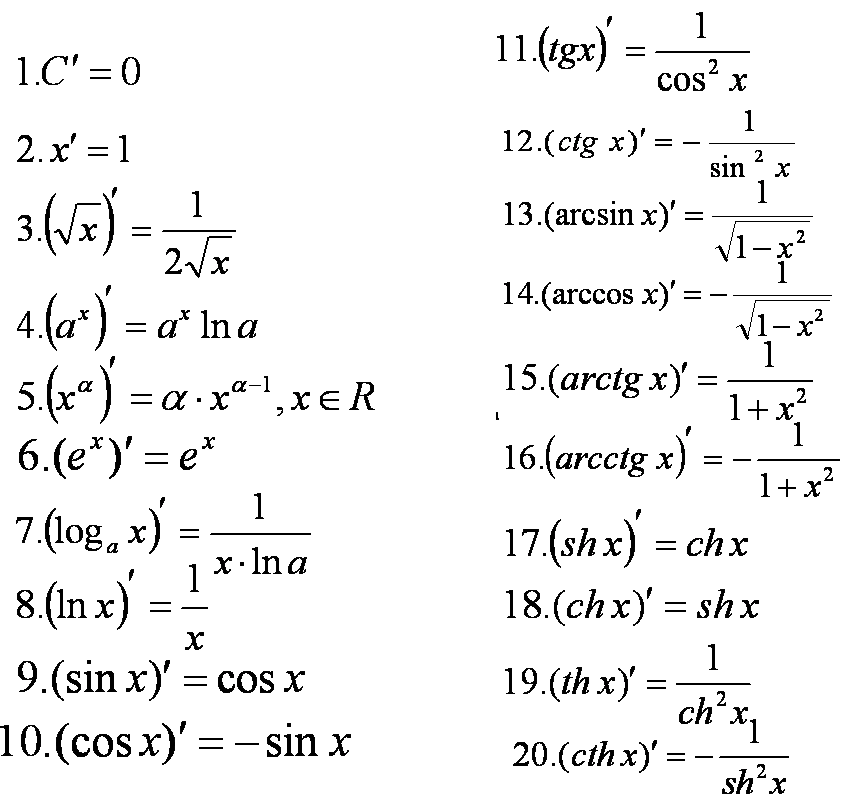
Вывод приведен в приложении

+ http://fmi.asf.ru/Library/Book/MatAn1/GLava4.html

#16 Т.о производной сложной функции: пусть y=f(u(x))-сложная функция и пусть u(x) – диф. в т.x, а f(u) – диф в т.u тогда:

y=f(u(x)) – так же диф в т.x а ее производная вычисляется по формуле: y'=f(x)*u'(x)

Док-во: При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:

Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).

Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0, Δy→0.

По условию  . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0) , где α→0 при Δu→0, а, следовательно, и при Δx→0.

Перепишем это равенство в виде:

Δy= y'_uΔu+α·Δu.

Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx

.

По условию  . Поэтому, переходя к пределу при Δx→0, получим y '_x= y '_u·u '_x.

Т. о производной обратной функции:

Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(y0), отличную от нуля, то в соответствующей точке x0=g(y0) функция y=f(x) имеет производную f '(x0), равную  , т.е. справедлива формула .

Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0.

Покажем, что  .

Пусть  . Тогда по свойству предела  . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е.  . Следовательно,

#17  Функция f(x) называется дифференцируемой в точке x, если ее приращение можно представить в виде y=A*x+o(x)*x, где A=const, lim(x0)(o(x))=0;

Линейная часть приращения функции, т.е. A*x  называется дифференциалом функции f(x) и обозначается df(x)=f(x)dx

Теорема(критерий): Чтобы ф-ия была диффер., необходимо, чтобы она имела в этой точке конечную производную.

Док-во: 1)Если y=f(x) - диффер., y=A*x+o(x)*x, y'=lim(x0)( y/x)=А;

2) lim(x00)(f(x))=f(x0),то o(x)= y/x-f'(x), принадлежит б/м ф-ии и o(x) 0, если x0, следовательно y=f'(x)*x+o(x)*x ;

Геометрический смысл: приращение

ординаты касательной. Dy=f’(x₀)dx; f’(x₀)=tg

Инвариантность:????????

#18 Теорема Ролля.

Пусть на отрезке [a,b] определена ф-ция f(x) причем: f(x) непрерывна на [a,b]; f(x) диф. на (a,b); f(a)=f(b). Тогда всегда найдется т.с(a,b), что f'(c)=0.

Геом. cмысл т Ролля: Если функция удв условиям теор. Ролля то сущ. Точка С на [a,b];касательная в этой точке параллельна оси X.

Теорема Ролля д-во: По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M>m.

Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю.

Пусть М>m. Так ка значения на концах отрезка равны, то  хотя бы одно из значений М или m функция принимает внутри отрезка [a, b]. Обозначим e, a < e < b точку, в которой f(e) = M. Так как М- наибольшее значение функции, то для любого Δx ( будем считать, что точка e + Δx находится внутри рассматриваемого интервала) верно: 

Δf(e) = f(e + Δx) – f(e)

При этом

 Но так как по условию производная в точке e существует, то существует и предел  .

Т.к.   и  , то можно сделать вывод:

 

#19 Теорема Лагранжа.

Пусть на отрезке [a,b] определена f(x), причем: f(x) непр. на [a,b]; f(x) диф. на [a,b]. Тогда найдется т-ка c(a,b) такая, что справедлива ф-ла (f(b)-f(a))/b-a= f'(c).

Геом.смысл теоремы Лагранжа:Если F (x) удв. усл. т.Лагранжа то сущ.хоть 1 точка С такая что касательная в этой точке || стягивающей хорде, стягивающая хорда - прямая соед. a и b.

Теорема Лагранжа д-во:

Док-во в приложении к документу

Теорема Коши.

Пусть ф-ции f(x) и g(x) непр. на [a,b] и диф. на

(a,b). Пусть кроме того, g`(x)0. Тогда  т-ка

с(a,b) такая, что справедл. ф-ла (f(b)-

f(a))/(g(b)-g(a))=f'(c)/g'(c).

Теорема Коши д-во: В приложении к документу

#20 Правило Лопиталя.

Если f(x) →0 и g(x) →0, при x→a,тогда lim(x→a)(f(x)/g(x))= lim(x→a)(f'(x)/g'(x))

Док-во: в приложении к документу