НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

им. Н.И. ЛОБАЧЕВСКОГО

В.А. Рябинин

Послеоптимизационный анализ задач линейного программирования

Лабораторная работа №4

вариант №18

Нижний Новгород

2005

1. Анализ чувствительности оптимального решения задачи к изменению свободных членов ограничений.

Фирма А выпускает изделия Х и поставляет их по договорным обязательствам фирме В ежемесячно в количестве 1000 шт. Каждое изделие состоит из двух деталей У и трех деталей Z. Детали У и Z можно купить в фирме С по цене соответственно 2 руб. и 1 руб. за шт. в объеме не более 800 и 1000 в месяц.

Детали можно также изготовить из заготовок U и V, закупаемых в фирме D по цене 4 и 7 руб. Из каждой заготовки U фирма Е за 2 руб. может изготовить 3 детали У и 1 деталь Z, а из заготовки V за 5 руб. – 3 детали У и 5 деталей Z, за 3 руб. – 5 деталей У и 2 детали Z.

Определить месячный план деятельности фирмы А, обеспечивающий выполнение договорных обязательств с минимальными затратами.

Обозначим за x₁- количество планируемых закупок деталей Y, в фирме C [шт] по 2 руб.

за x₂- количество планируемых закупок деталей Z, в фирме C [шт] по 1 руб.

за x₃- количество купленных деталей U, в фирме D [шт] по 4 руб. и преобразованные в 3Y и 1Z в фирме E за 2 руб.

за x₄- количество купленных деталей V, в фирме D [шт] по 7 руб. и преобразованные в 3Y и 5Z в фирме E за 5 руб.

за x₅- количество купленных деталей V, в фирме D [шт] по 7 руб. и преобразованные в 5Y и 2Z в фирме E за 3 руб.

Ограничения по закупкам в фирме C запишутся так:

x ₁≤800 (1)

x₂≤1000 (2)

Ограничение по количеству необходимых деталей Y

x₁+3*x₃+3*x₄+5*x₅=2000 (3)

Ограничение по количеству необходимых деталей Z

x₂+x₃+5*x₄+2*x₅=3000 (4)

Запишем полученную систему:

x₁≤800

x₂≤1000 (5)

x₁+3*x₃+3*x₄+5*x₅=2000

x₂+x₃+5*x₄+2*x₅=3000

x_i≥0, i=1..5

Оптимизационным критерием F будут затраты, которые необходимо минимизировать:

F=2*x₁+x₂+6*x₃+12*x₄+10*x₅→min (6)

Тогда решением будет вектор x^*(x₁,x₂, x₃,x₄,x₅), если на нем достигается минимальное значение критерия F.

Запишем систему (5) в каноническом виде:

x ₁+x₆=800

x₂+x₇=1000 (7)

x₁+3*x₃+3*x₄+5*x₅=2000

x₂+x₃+5*x₄+2*x₅=3000

x_i≥0, i=1..7

Решим задачу методом искусственного базиса. Для этого составим вспомогательную задачу:

F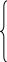 =x₈+x₉→min

x₁+x₆=800

x₂+x₇=1000 (8)

x₁+3*x₃+3*x₄+5*x₅+x₈=2000

x₂+x₃+5*x₄+2*x₅+x₉=3000

x_i≥0, i=1..9

Решим методом искусственного базиса:

Оптимальная симплекс таблица:

		2	1	6	12	10			M	M
Cb	БП	x1	x2	x3	x4	x5	x6	x7	x8	x9	b
0 1 10 12	x6 x2 x5 x4	1 0 0.2631 -0.105	0 1 0 0	0 0 0.6315 -0.052	0 0 0 1	0 0 1 0	1 0 0 0	0 1 0.1578 -0.263	0 0 0.2631 -0.105	0 0 -0.157 0.2631	800 1000 210.526 315.789
	ƒ	-0.631	0	-0.315	0	0	0	-0.578	1.368 -M	1.578 -M	6894.73

Экономическая интерпретация:

Необходимо купить 1000 деталей Z в фирме C по 1 руб.;

315.789 деталей V в фирме D по 7 руб. и изготовить из каждой по 3 детали Y и 5 детали Z за 5 руб. в фирме E;

210.516 деталей V в фирме D по 7 руб. и изготовить из каждой по 5 деталей Y и 2 детали Z за 3 руб. в фирме E;

Минимальные затраты:

1000[шт]*1[руб]+315.789[шт]*12[руб]+ 210.516 шт]*10[руб]= =6894.73[руб]

Двойственные оценки:

y*=(0; 0.578947; 1.36842; 1.57894)

Теперь найдём устойчивости двойственных оценок – область, в которой при изменении свободных членов ограничений двойственные оценки не меняются. Неизменность двойственных оценок говорит о том, что не меняют своих номеров базисные и свободные переменные в решении.

Изначально мы учитывали изменение знаков неравенств (1) и (2), но знаки самих неравенств не меняли. Сейчас мы также не будем менять знаки первого и второго неравенств, но примем во внимание обратный знак Δb_1,2 при расчёте конкретных значений.

Пусть свободные члены ограничений изменились на Δb₁, Δb₂, Δb₃, Δb₄ соответственно. Тогда оптимальное решение новой задачи будет находиться так:

X’_B=B^-1*b’=B^-1*b+B^-1*Δb=X_B+B^-1*Δb

Базисное решение вычисляется через матрицу, обратную к базисной, и свободные члены ограничений. Из оптимальной симплекс-таблицы получим матрицу, обратную к базисной, и оптимальное решение (базисные компоненты):

800

1000

210.526

315.789

1	0	0	0
0	1	0	0
0	0.1578	0.2631	-0.157
0	-0.263	-0.105	0.2631

Δb1

Δb2

Δb3

Δb4

X

+

*

’_B=

X ₆=800+Δb₁>0

X₂=1000+ Δb₂>0 (9)

X₅=210.526+ 0.1578*Δb₂+0.2631* Δb₃-0.157* Δb₄>0

X₄=315.789- 0.2631*Δb₂-0.105* Δb₃+0.2631* Δb₄>0

Все элементы решения должны быть неотрицательны, иначе решение будет недопустимым, т.е. базисное решение остаётся оптимальным до тех пор, пока оно допустимое. Область устойчивости следующая:

8 00+Δb₁>0

1000+ Δb₂>0 (10)

210.526+ 0.1578*Δb₂+0.2631* Δb₃-0.157* Δb₄>0

315.789- 0.2631*Δb₂-0.105* Δb₃+0.2631* Δb₄>0

Интервалы устойчивости:

1) Δb₁≠0; Δb₂= Δb₃= Δb₄=0

8 00+Δb₁>0

1000>0 => Δb₁Є[-800;∞] b₁Є[0;∞]

210.526 >0

315.789 >0

2) Δb₂≠0; Δb₁= Δb₃= Δb₄=0

8 00>0

1000+ Δb₂>0 =>Δb₂Є[-1000;1200,2623]

210.526+ 0.1578*Δb₂ >0 b₂Є[0;2200,2623]

315.789- 0.2631*Δb₂ >0

3) Δb₃≠0; Δb₁= Δb₂= Δb₄=0

8 00>0

1000>0 =>Δb₃Є[-800,1748;3007,5143]

210.526+ 0.2631* Δb₃ >0 b₃Є[1199,8252; 5007,5143]

315.789-0.105* Δb₃ >0

4) Δb₄≠0; Δb₁= Δb₂= Δb₃=0

8 00 >0

1000 >0 =>Δb₄Є[-1200,2623;1340,9299]

210.526 -0.157* Δb₄>0 b₄Є[1799,7377; 4340,9299]

315.789+0.2631* Δb₄>0

Экономический смысл:

При данных изменениях ресурсов двойственные оценки не изменятся, а значит и номера базисных переменных также не изменятся:

1) При изменении количества запасов деталей Y в фирме С от 0 до бесконечно больших запасов.

2) При изменении запасов фирмы C деталей Z от 0 до 2200,2623

3) При изменении норм производства одной детали X из от 1,1998 до 5,0075 деталей Y и от 1,7997 до 4,3409 деталей Z

4) Изменение обязательств перед фирмой B от 599,9126 до 1446,9766 деталей X

Изобразим область устойчивости двойственных оценок к изменению свободных членов ограничений графически. Для этого, исходя из экономических соображений и наглядности графика, построим его в координатах Δb₁, Δb₂, т.е. Δb₃= Δb₄=0

8 00+Δb₁>0 (11)

1000+ Δb₂>0 (12)

210.526+ 0.1578*Δb₂ >0 (13)

315.789- 0.2631*Δb₂ >0 (14)

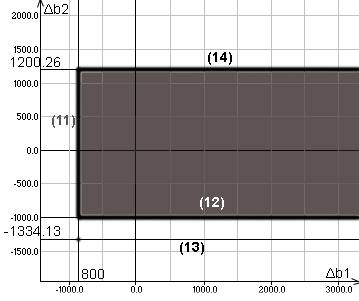
Пример практического применения интервалов устойчивости.

Изменим условие задачи:

Фирма C может продать 2000 деталей Z

Интервал устойчивости b₂Є[0;2200,2623] 2000 деталей Z входят в этот интервал. А значит, двойственные оценки не изменятся.

Δb₂=1000

X6

X2

X5

X4

800

1000+ Δb2

210.526+ 0.1578*Δb2

315.789- 0.2631*Δb2

800

2000

368.326

52.689

X’_B= =

Решение является допустимым, а значит, и оптимальным. Значение критерия найдём по третьей теореме двойственности:

ΔF=y^*₂*Δb₂=-0.578947*1000=-578.947 F=6894.73-578.947=6315.783