Основные характеристики систем связи с разнесенным приемом

Методические указания к лабораторной работе

1. Цель работы

Изучение основных методов разнесённого приема: когерентного приема сигналов и приема сигналов с отбором «лучшей» антенны. Анализ статистических свойств отношения сигнал/шум (ОСШ) в многолучевом канале с некоррелированными релеевскими замираниями сигналов при использовании этих методов. Определение вероятности битовой ошибки.

2. Краткие сведения из теории

2.1. Когерентный прием сигналов

Рассмотрим пространственный разнесенный прием сигналов с помощью N-элементной антенной решетки (АР), схема которой показана на рис. 1.

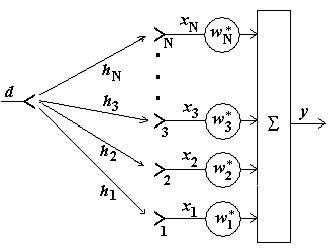
Рис. 1 Разнесенный прием сигналов

Если передается сигнал d, то вектор X сигналов в приемных антеннах равен

(1.1)

где P₀ – мощность передатчика, - вектор-столбец состоящий из коэффициентов передачи для каждой приемной антенны, (.)^T - знак транспонирования, Z – вектор собственных шумов.

Шумы в различных приемных антеннах будем считать не коррелированными между собой, то есть корреляционная матрица шума <ZZ^H>=₀²I, где I – единичная матрица, ₀² – мощность шума, одинаковая в каждой антенне, (.)^H – обозначает эрмитовое сопряжение.

Принятые сигналы суммируются с комплексными весовыми коэффициентами, которые объединим в весовой вектор . Тогда результирующий сигнал равен

. (1.2)

Найдем выходное ОСШ. Из (1.2) получим что

. (1.3)

где - среднее ОСШ в случае одной приемной антенны.

ОСШ не зависит от нормировки весового вектора W. Удобно нормировать вектор W так, что W^HW=1. В результате для ОСШ будем иметь

. (1.4)

Из (1.4) следует, что для обеспечения максимума ОСШ вектор W должен быть параллелен вектору H коэффициентов передачи (W=H), так как скалярное произведение векторов W и H будет наибольшим, когда они параллельны друг другу. Из условия нормировки весового вектора следует, что .

В таком весовом векторе обеспечивается согласованный (когерентный) прием сигналов и выходное ОСШ будет равно

. (1.5)

Отсюда следует, что выходное ОСШ представляет собой сумму ОСШ в каждой антенне.

Плотность вероятности ОСШ  зависит от статистических свойств замираний сигналов. В случае некоррелированных релеевских замираний сигналов одинаковой мощности дисперсия канальных коэффициентов является одинаковой во всех антеннах и ОСШ  имеет хи-квадрат распределение с 2N степенями свободы вида

. (1.6)

где - среднее ОСШ в каждой приемной антенне.

На рис. 2 показано хи-квадрат распределение для разного числа N приемных антенн (N=1, 2 и 4) при ₀=1 (сплошные кривые). Среднее ОСШ на выходе АР равно . Поэтому с ростом N соответствующие кривые сдвигаются вправо. Более того, видно, что вероятность глубоких замираний сигналов (малых ОСШ) значительно уменьшается при увеличении N.

Рис. 2. Плотность вероятности ОСШ для разного числа антенн при когерентном суммировании антенн (сплошные кривые) и отборе «лучшей» антенны (пунктирные кривые)

Будем рассматривать сигналы двоичной фазовой модуляции. Вероятность битовой ошибки в системе с разнесенным приемом зависит от статистических свойств замираний сигналов в приемных антеннах. Чтобы найти вероятность BER битовой ошибки необходимо функцию f() из (1.6) подставить в следующий интеграл:

, (3.1)

где BER() – вероятность битовой ошибки в гауссовском шумовом канале без замираний сигналов при ОСШ равном .

Вероятность BER() равна

, (3.2)

где (x) - интеграл вероятности

. (3.3)

В результате будем иметь, что

. (3.4)

После интегрирования, получим выражение для вероятности битовой ошибки в явном виде

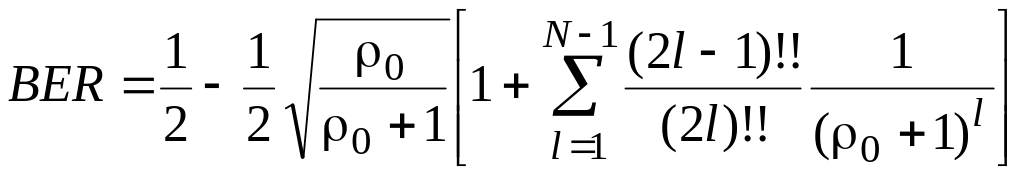, (3.5)

где (2l-1)!! = 135...(2l-1); (2l)!! = 246...2l.

При произвольном числе антенн и больших ОСШ формула (3.5) упрощается и принимает следующий вид:

. (3.6)

Рассмотрим некоторые частные случаи.

а) Мощность сигнала стремится к нулю (₀0), то есть имеется только собственный шум. Вероятность ошибки стремится к 1/2 (BER1/2) независимо от числа приемных антенн.

б) Имеется одна приемная антенна (N=1). Нетрудно получить из (3.5), что вероятность битовой ошибки будет равна

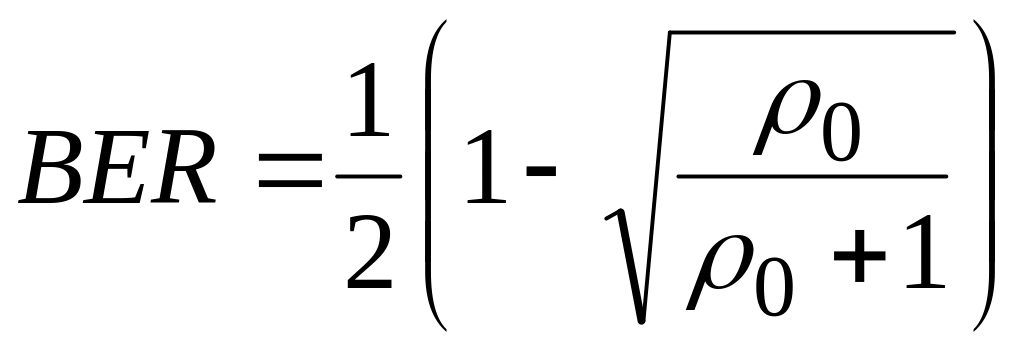. (3.7)

В случае больших ОСШ (₀>>1) из(3.6) следует приближенное выражение

. (3.8)

с) Число антенн равно двум (N=2). Из (3.5) имеем, что

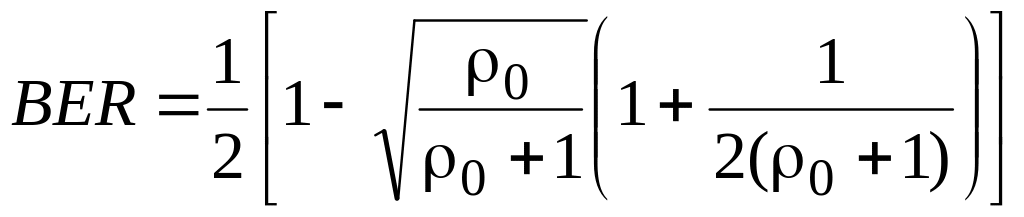. (3.9)

При больших ОСШ получим, что

. (3.10)

д) Число антенн равно четырем (N=4). Из (3.5) найдем, что

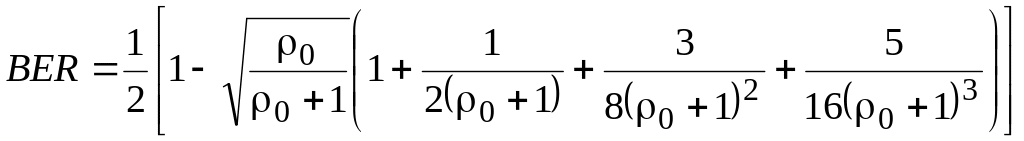. (3.11)

При больших ОСШ

. (3.12)

е) Число антенн равно восьми (N=8). При больших ОСШ имеем

. (3.13)

Нетрудно видеть из приведенных примеров, что вероятность ошибки уменьшается обратно пропорционально ОСШ в степени, равной числу приемных антенн, то есть BER₀^N. Поэтому в логарифмическом масштабе кривые вероятности ошибок имеют линейную асимптотику при больших ОСШ с углом наклона прямых равным (N). Этот угол наклона, называется порядком разнесения при приеме на АР.

Кривые вероятности ошибок в зависимости от ОСШ для разного числа антенн (N=1,2,4 и 8) представлены на рис. 4.

Рис. 4. Вероятности битовой ошибки в зависимости от ОСШ для 1, 2, 4 и 8-ми приемных антенн

Оценим ОСШ, необходимое для обеспечения заданной вероятности ошибки, например, равной 0,01. Результаты оценки показаны в таблице 1. Видно, что с ростом числа антенн необходимое ОСШ значительно уменьшается, то есть имеет место энергетический выигрыш, который обеспечивается двумя факторами. Первый - связан с увеличением среднего уровня принимаемого сигнала за счет использования N приемных антенн (выигрыш за счет усиления). Второй - с уменьшением вероятности глубоких замираний сигналов при приеме на множество антенн, когда вероятность одновременного замирания сигналов во всех антеннах уменьшается с ростом их числа (выигрыш за счет разнесенного приема).

Таблица 1.

Число антенн	Требуемое ОСШ, дБ	Выигрыш в ОСШ, дБ	Выигрыш за счет усиления, дБ	Выигрыш за счет разнесения, дБ
N=1	13,8	-	-	-
N=2	5,4	8,4	3	5,4
N=4	0,2	13,6	6	7,6
N=8	-3,7	17,5	9	8,5

2.2. Прием сигналов с отбором «лучшей» антенны

Рассмотрим метод отбора «лучшей» антенны, который не является оптимальным. Однако он наиболее прост для практической реализации, так как предполагает использование только одного высокочастотного приемного устройства. В каждый момент времени сравниваются мгновенные ОСШ на выходе каждой приемной антенны, и отбирается та антенна, которая имеет наибольшее ОСШ. Выходы остальных антенн отключаются.

Выходное ОСШ в в i-ой антенне подчиняется экспоненциальной плотности вероятности, которая получается из (1.6) при N=1 и имеет вид

. (2.1)

Поэтому, вероятность того, что ОСШ в этой антенне будет меньше или равно некоторого значения  равна

. (2.2)

Вследствие статистической независимости замираний сигналов в отдельных антеннах вероятность того, что ОСШ одновременно во всех N антеннах будет меньше или равно  будет определяться выражением:

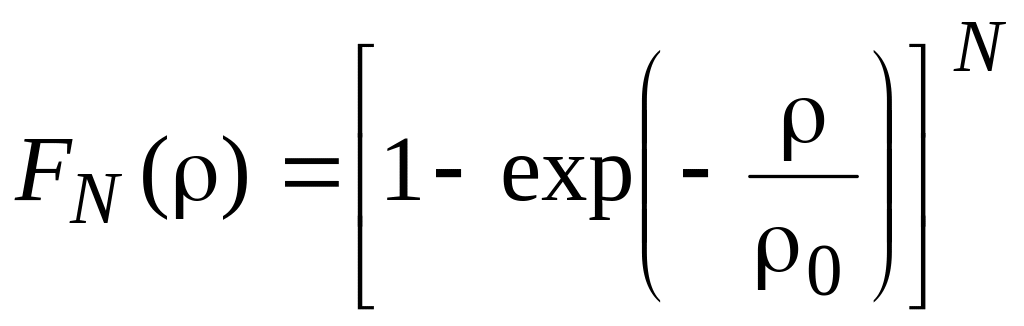. (2.3)

Вероятность того, что ОСШ как минимум в одной антенне будет превышать значение  равно

. (2.4)

Чтобы найти плотность вероятности выходного ОСШ при отборе «лучшей» антенны продифференцируем интегральную функцию распределения по аргументу . В результате будем иметь, что

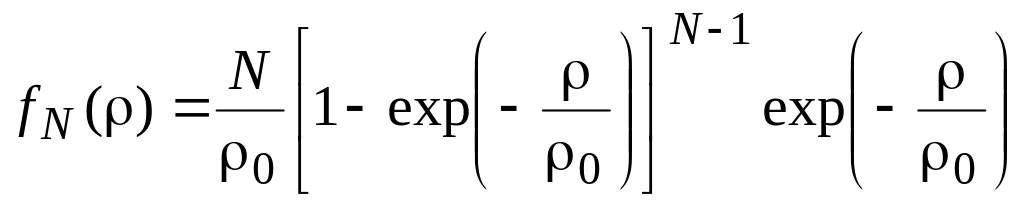. (2.5)

На рис. 2 показано распределение (2.5) для разного числа N приемных антенн (N=1, 2 и 4) при ₀=1 (пунктирные кривые). Видно, что для одинакового N плотность вероятности ОСШ при отборе «лучшей» антенны сдвигается влево по сравнению с кривой, соответствующей когерентному суммированию, то есть вероятность замираний сигналов (малых ОСШ) увеличивается.

Среднее ОСШ при отборе «лучшей антенны» будет равно

. (2.6)

Обозначим . Тогда интеграл (2.6) с учетом (2.5) можно преобразовать к виду

. (2.7)

Сделаем замену переменных . Отсюда . Далее учтем разложение натурального логарифма в бесконечный ряд. В результате получим, что

. (2.8)

или

. (2.9)

Это выражение можно преобразовать следующим образом

. (2.10)

На рис. 3 показаны потери в среднем ОСШ для метода отбора «лучшей» антенны по сравнению с методом когерентного суммирования сигналов во всех антеннах, когда . Видно, что эти потери могут составлять достаточно большую величину. Например, при числе антенн N=4 они равны 2.84 дБ.

Рис. 3. Потери в среднем ОСШ при отборе «лучшей» антенны по сравнению с когерентным суммированием всех антенн

Чтобы найти вероятность битовой ошибки плотность вероятности (2.5) подставим в интеграл (3.1) и учтем выражение (3.2) для вероятности ошибки в гауссовском шумовом канале. В результате будем иметь, что

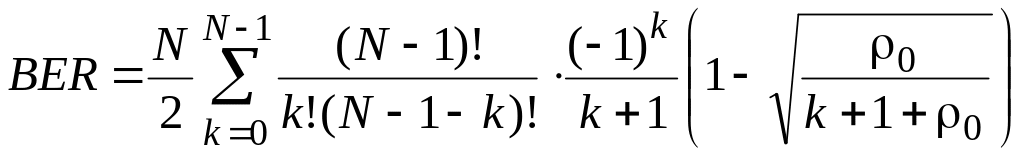. (3.17)

В случае двух приемных антенн (N=2) и при больших ОСШ получим, что

. (3.18)

Из сравнения (3.18) с (3.10) следует, что вероятность битовой ошибки для одинакового ОСШ при отборе «лучшей» антенны в два раза больше, чем при когерентном суммировании сигналов двух антенн.

Кривые вероятности битовой ошибки в зависимости от ОСШ для метода отбора «лучшей» антенны при разном числе антенн (N=1,2,4 и 8) представлены на рис. 6.

Рис. 6. Вероятность битовой ошибки в зависимости от ОСШ для разного числа приемных антенн (N=1,2,4 и 8)

Оценим ОСШ, необходимое для обеспечения заданной вероятности битовой ошибки, например, равной 0.001. Получим, что ОСШ должно быть 13,8; 6,8; 3,3 и 1,3 дБ для числа приемных антенн N=1,2,4 и 8, соответственно. Сравнивая эти данные с результатами таблицы 1 для системы с когерентным суммированием выходных сигналов антенн, можно увидеть, что при использовании метода отбора «лучшей» антенны требуемое ОСШ становится большим на 1,4; 3,1 и 5,0 дБ при N=2,4 и 8, соответственно. Таким образом, с ростом числа антенн разница в эффективности этих двух методов увеличивается.